6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

7) Периодичность функции.

Функция f(x) - периодичная, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.

Тема 2. Пределы и непрерывность

6. Предел числовой последовательности

предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины

Число называется пределом числовой последовательности , если последовательность является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

7. Предел функции в бесконечности

Число А называется пределом функции f (x) при х → ∞, если для любого как угодно малого положительного числа ε, найдётся зависящее от этого ε большое положительное число К, такое, что для всех значений аргумента, больших по величине этого числа К, значения функции отличаются по величине от указанного числа А меньше, чем на ε

8. Предел функции в точке

Число A называется пределом функции y=f(x), при х->x0, если для всех значений x, достаточно мало отличающихся от числа x0, соответствующие значения функции f(x) как угодно мало отличаются от числа A.

9. Бесконечно малая величина

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

10. Бесконечно большая величина

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

11. Связь между б.м. и б.б. величинами

12. Свойства пределов

Рассмотрим основные свойства пределов.

1. Предел суммы

Предел суммы равен сумме пределов, если каждый из них существует, т.е.

2. Предел разности

Предел разности равен разности пределов, если каждый из них существует, т.е.

3. Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

4. Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

5. Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.

6. Предел частного

Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.

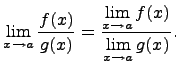
13. Замечательные пределы

Первый замечательный предел:

Второй замечательный предел:

14. Непрерывность функции

Функция называется непрерывной в точке х_о если выполняются три условия:

1. Функция определена в точке х_о

2. В этой точке существует конечный предел функции

3. Предел точки х_о равен значению функции в этой точке

Функция непрерывна на интервале, если она непрерывна в каждой точке этого интервала.

Тема 3. Производная и дифференциал

15. Производная функции

Производной функции y=f(x) в точке x₀ называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю.

16. Зависимость между дифференцируемостью и непрерывностью функции

Если функция дифференцируема в точке, то она в этой точке непрерывна. Обратное не верно.

17. Геометрический и физический смысл производной