5 Ряды в комплексной области

5.1 Числовые ряды

Рассмотрим ряд с комплексными членами

. (58)

Теорема. Для сходимости ряда необходимо и достаточно, чтобы сходились оба ряда:

( )

( )

Определение. Ряд (58) называется абсолютно сходящимся, если сходится ряд

(59)

Ряды ( ), ( ) и (59) являются рядами с действительными членами, и вопрос об их сходимости решается с помощью известных признаков сходимости рядов в действительной области.

Пример 1. Исследовать на сходимость ряд .

а) имеем . Таким образом, вопрос о сходимости данного ряда сводится к вопросу о сходимости рядов с действительными членами и . Так как каждый из рядов сходится абсолютно, то и данный ряд сходится абсолютно;

б) приведем другое решение. Исследуем ряд на абсолютную сходимость, для чего составим ряд – этот ряд сходится абсолютно.

Пример 2. Исследовать поведение ряда .

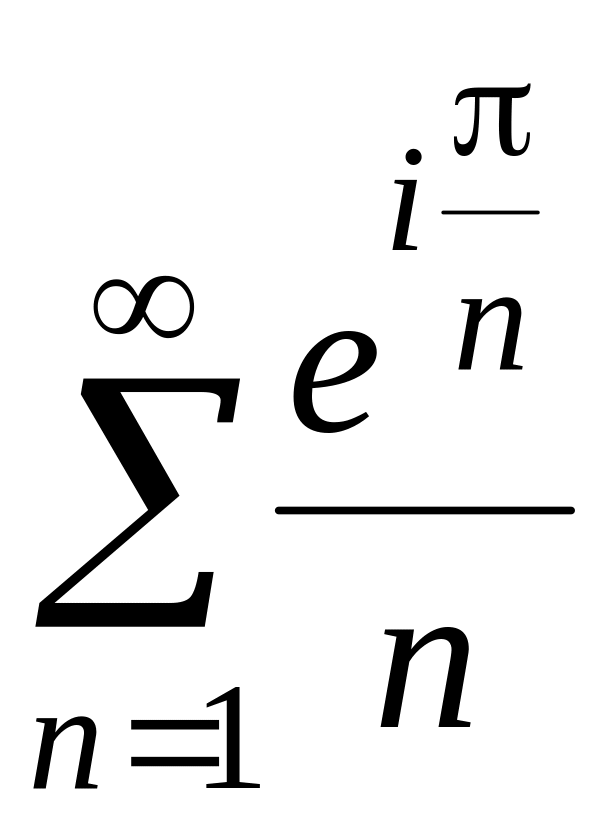Так как ряд 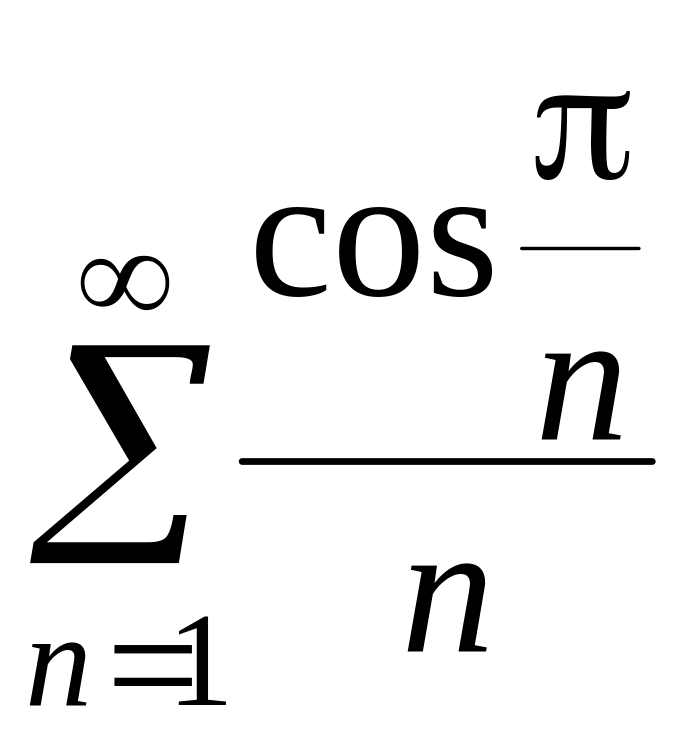расходится, то расходится и исходный ряд.

5.2 Степенные, сходящиеся к ним и двусторонние ряды

Определение 1. Ряд вида

, (60)

где – комплексные постоянные, a – комплексная переменная, называется степенным рядом в комплексной области.

Определение 2. Ряд вида

(61)

называется степенным рядом общего вида.

Определение 3. Ряд вида

(62)

называется рядом, сходящимся к степенному общего вида.

Определение 4. Двусторонним называется ряд вида

. (63)

Область сходимости степенного ряда (58) есть круг с центром в начале координат: , где – радиус сходимости. В некоторых cлучаях он может быть определен по формулам

а) ; б) 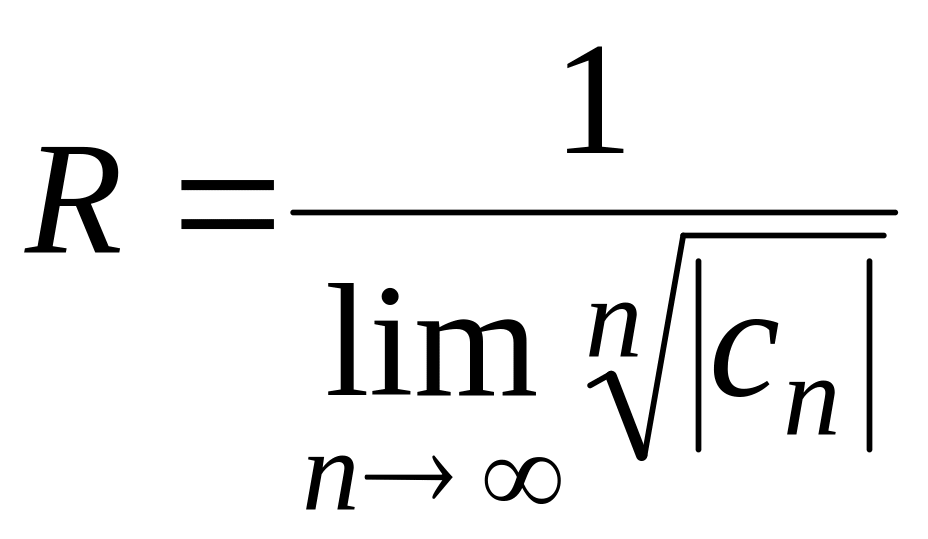. (64)

Для рядов (61) областью сходимости служит круг . Область сходимости ряда (62) ищется после проведения замены: . Ряд вида (63) сходится в области, в которой сходятся ряды

(65)

(66)

Пусть ряд (65) сходится в области , т.е. вне круга с центром в точке и радиуса , а ряд (66) в круге . Тогда, если: 1) , то ряд (63) расходится всюду; 2) , то ряд (63) сходится в кольце . Здесь , .

Пример 1. Найти радиус сходимости степенного ряда .

Находим модуль коэффициента . Применяя формулу б) из (64), находим .

Пример 2. Найти область сходимости ряда .

Имеем , и

. Следовательно, ряд сходится в области , т.е. вне круга с центром в точке радиуса .

Пример 3. Определить область сходимости ряда .

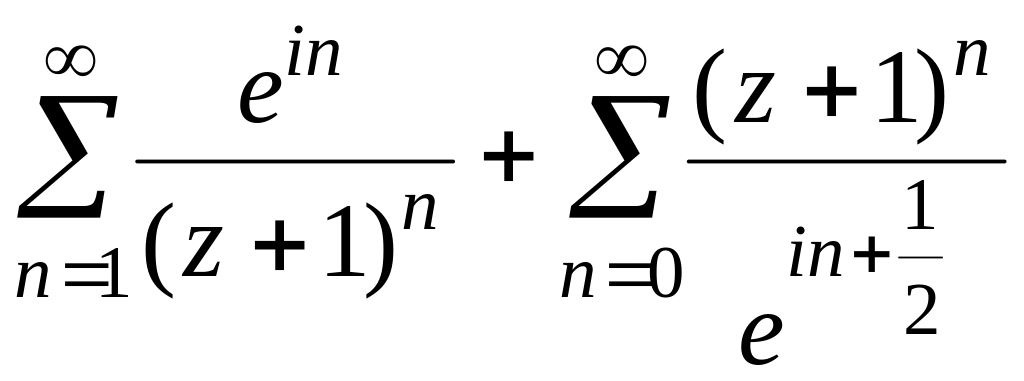Для ряда имеем .

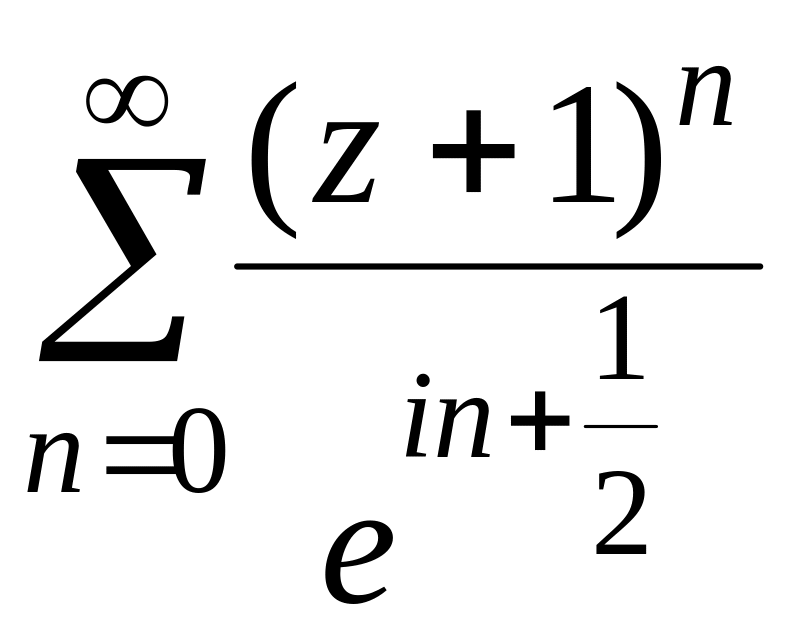Следовательно, . Первый ряд сходится в области . Для степенного ряда имеем , . Его радиус сходимости 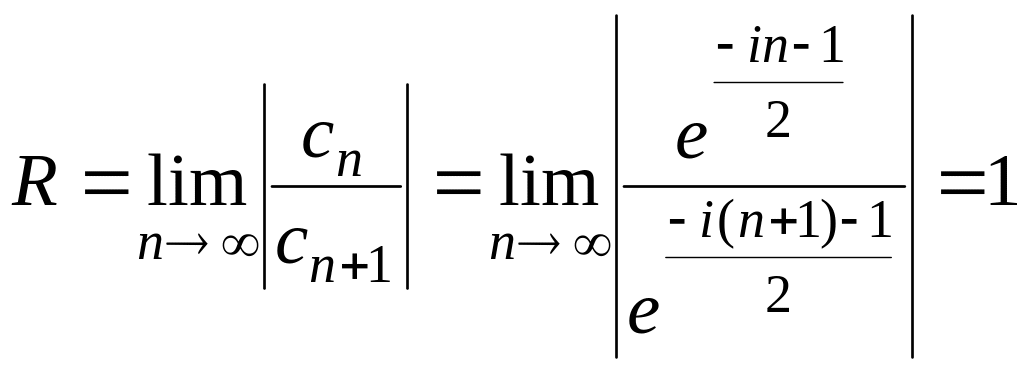, т.е. второй ряд сходится в области . Данный ряд расходится всюду.

Пример 4. Определить область сходимости ряда .

Для первого из рядов имеем , Следовательно, . Первый ряд сходится в области . Для второго ряда имеем . Радиус его сходимости – он сходится в области . Таким образом, данный ряд сходится в кольце .

5.3 Ряды Тейлора и Лорана

5.3.1 Ряд Тейлора

Однозначная и аналитическая в точке функция разлагается в окрестности этой точки в степенной ряд – ряд Тейлора

, (67)

где коэффициенты вычисляются по формулам

. (68)

Здесь – окружность с центром в точке , целиком лежащая в области аналитичности . Областью сходимости ряда является круг c центром в точке разложения радиуса . Этот радиус равен расстоянию от центра разложения до ближайшей особой точки – точки, в которой теряет аналитичность. В круге сходимости этого ряда суммой его является функция .

Теорема Тейлора. Функция , аналитическая в круге , однозначно представима в нем своим рядом Тейлора (67), коэффициенты которого определяются по формулам (68).

Из этой теоремы и теоремы о возможности дифференцирования степенного ряда в круге сходимости любое число раз следует, что разложение функции в степенной ряд единственно. Это означает, что по любому методу разложения функции в степенной ряд мы получаем одно и то же разложение – ряд Тейлора. При ряд (67) называется рядом Маклорена.

При решении многих задач рекомендуется пользоваться следующими разложениями элементарных функций:

1) 2) , 3) , 4) 5) ; 6) ; 7) ; 8) .

(69)

Пример 1. Разложить в ряд по степеням функцию .

Рассмотрим сначала следующее преобразование данной логарифмической функции: . Воспользуемся разложением 4) из (69) для , полагая . Так как разложение 4) имеет место при , то наше разложение будет иметь место при . Таким образом, для .

Часто при разложении функций в ряд удобно пользоваться дифференцированием или интегрированием известных разложений, а при разложении рациональной дроби – разложением ее на простейшие.

Пример 2. Разложить в ряд по степеням функцию .

Разложим на простейшие дроби: .

По формуле суммы геометрической прогрессии 7) из (69) получаем:

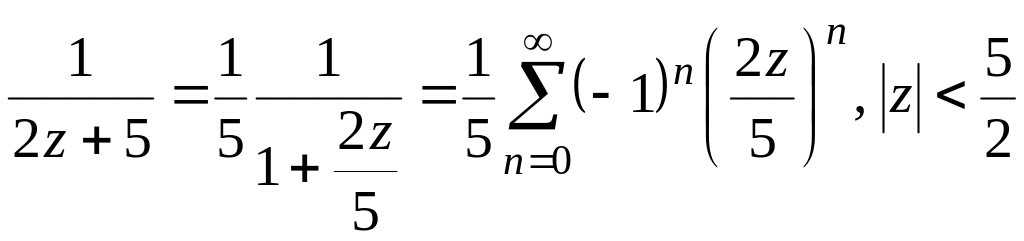и .

замечая, что , и применяя теорему о возможном почленном дифференцировании степенного ряда в круге сходимости получаем:

.

Складывая ряды для и , получаем .