Тема 11. Статистичні методи Вимірювання зв’язків

1.При функціональному зв’язку кожному конкретному значенню факторної ознаки відповідає

б) конкретне значення результативної ознаки;

2. При стохастичному зв’язку кожному конкретному значенню факторної ознаки відповідає:

а) певна множина результативної ознаки;

3. При кореляційному зв’язку кожному конкретному значенню факторної ознаки відповідає:

в) середнє значення результативної ознаки.

4. За напрямком зв’язки поділяються на:

б) прямі;

5. Прямий – це такий зв’язок між факторною та результативною ознаками, за якого:

а) зі збільшенням факторної ознаки результативна збільшується;

6. Зворотний – це такий зв’язок між факторною та результативною ознаками, за якого:

б) зі збільшенням факторної ознаки результативна зменшується;

7. На першому етапі аналізу кореляційного зв’язку при обґрунтуванні моделі постають такі питання:

а) вибір факторної ознаки;

8. Оцінка щільності зв’язку за методом аналітичного групування ґрунтується на:

б) правилі складання дисперсій;

9. Відношення міжгрупової дисперсії до загальної називається:

г) кореляційним відношенням.

10. У кореляційно-регресивному аналізі оцінка лінії регресії здійснюється:

б) в кожній точці інтервалу зміни факторної ознаки;

11. За формою зв’язки поділяють на:

а) лінійні та нелінійні;

12. Кореляційне відношення являє собою частку:

г) міжгрупової дисперсії у загальній

13. Щільність зв’язку при кореляційно-регресивному аналізі оцінюється:

а) кореляційним відношенням;

14. Для оцінки щільності лінійного зв’язку при кореляційно-регресивному аналізі використовується:

в) лінійний коефіцієнт кореляції

15. Лінійний коефіцієнт кореляції змінюється в межах:

а) від – 1 до + 1;

16. Кореляційне відношення змінюється в межах:

в) від 0 до + 1;

17. Коефіцієнт детермінації змінюється в межах:

в) від 0 до + 1;

18. Якщо кореляційне відношення дорівнює нулю, це свідчить про:

г) відсутність зв’язку.

19. Якщо лінійний коефіцієнт кореляції дорівнює +1, це свідчить про:

б) прямий функціональний зв’язок;

20. Якщо лінійний коефіцієнт кореляції дорівнює (–1), це свідчить про:

г) зворотний функціональний зв’язок.

21. Непараметричні методи оцінки щільності зв’язку використовуються:

а) для попереднього аналізу наявності та оцінки щільності зв’язку;

б) для визначення наявності та щільності зв’язку між якісними ознаками;

Відповіді 4) а, б;

22. Коефіцієнт збігу знаків змінюється в межах:

б) від – 1 до + 1;

23. Коефіцієнт кореляції рангів Спірмена змінюється в межах:

б) від – 1 до + 1;

24. Коефіцієнт збігу знаків показує:

б) щільність зв’язку;

в) напрямок зв’язку.

Відповіді: 6) б, в;

25. Коефіцієнт кореляції рангів Спірмена встановлює:

в) напрямок зв’язку.Відповіді3) в;

26. Коефіцієнт взаємної спряженості, який визначається за формулою:

,називається коефіцієнтом:

б) Чупрова;

27. Коефіцієнт взаємної спряженості, який визначається за формулою:

,

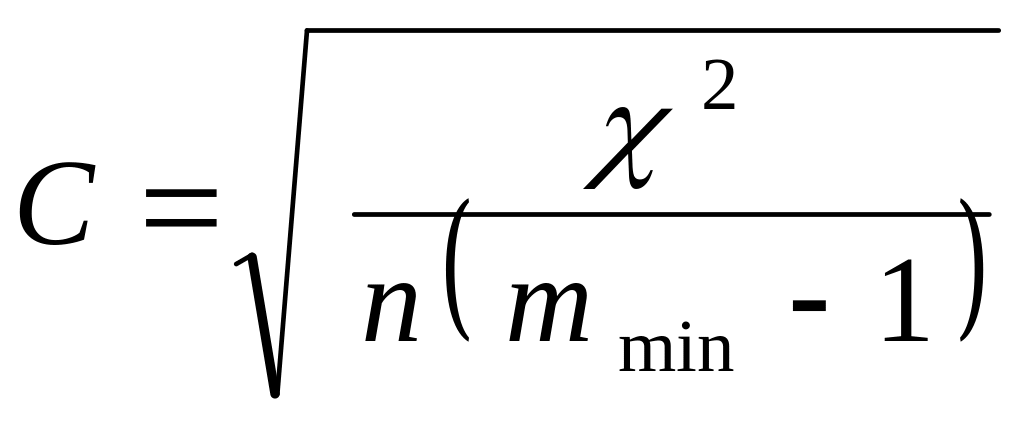називається коефіцієнтом:

а) Крамера;

28. Міру відносного ризику характеризує:

б) відношення шансів;

29. Коефіцієнт колігації був запропонований:

в) Юлом.

30. Якщо коефіцієнт збігу знаків К = – 1, це означає, що зв’язок;

в) зворотній функціональний.

31. Для аналізу 4-клітинкової таблиці взаємної спряженості використовуються коефіцієнти:

а) контингенції, асоціації, колігації;

32. Якщо коефіцієнт збігу знаків К = 0,2:

б) зв’язок вважається не доказаним;

Відповіді: 2) б;

33. Зв’язок вважається істотним, якщо розраховане значення коефіцієнта, за допомогою якого оцінюється зв’язок між ознаками:

в) більше за критичне значення.

34. Зв’язок між ознаками прямий функціональний, якщо:

б) коефіцієнт кореляції рангів Спірмена дорівнює 1;