Задачи для самостоятельного вычисления

В качестве примера реализации простых вычислений в MS Excel рассмотрим следующую задачу.

Задача 1. Заполните таблицу формулами, для расчета комиссионных и общей стоимости товара.

Рис.7. Таблица исходных данных для расчетов

Задача 2. Вычислить сопротивления последовательно соединенных резисторов и силы тока при заданном напряжении.

Исходные данные

Цепь постоянного тока, состоящая из трех последовательно соединенных сопротивлений R1, R2, R3 с постоянным напряжением U на зажимах.

Модель решения задачи

Общее сопротивление в последовательной цепи вычисляется по формуле R=R1+R2+R3, а ток - по формуле I=U/R.

Решение задачи

1. Исходные значения сопротивлений вводятся в ячейки B3, D3, F3, а значение напряжения - в ячейку D10 (рис.8).

Рис.8. Вычисление сопротивления и силы тока

2. В ячейки D11 и D12 вводятся формулы согласно таблицы 2.

Таблица 2.

Адрес ячейки	Содержимое ячейки
D12	=СУММ(В3, D3, F3)
D11	=D10/D12

При оформлении задачи было применено следующее форматирование:

• изображения резисторов получены с применением выделения соответствующих ячеек рамкой ГлавнаяЯчейкиФормат ячеекГраницы;

• линии соединения между резисторами и место подключения источника питания созданы с помощью элементов рисования ВставкаИллюстрацииФигурыЛинии;

• одни данные в ячейках выровнены по центру, другие - по правому или левому краю: U=, I=, R= ‑ выровнены по правому краю, а В, А, Om – по левому краю.

Результат решения задачи приведен на рис.8.

Контрольные вопросы

1. Оформление таблиц в Microsoft Excel.

2. Использование автофункций, способы автозаполнения.

3. Принципы использования формул в Microsoft Excel.

4. Построение простейших диаграмм.

Лабораторная работа № 2 Табулирование функций одной переменной и построение их графиков с помощью электронных таблиц

Абсолютные и относительные ссылки. При копировании формул из одной ячейки в другую в Excel автоматически меняются ссылки на ячейки, т.е. сохраняется относительное расположение ячеек результата и ячеек операндов. Такая адресация называется относительной.

В тех случаях, когда адрес ячейки операнда не должен меняться, ис­пользуют абсолютную адресацию, записывая перед номером строки и столбца знак $. Знак вводится клавишей F4. Например, $А$7 ‑ абсолютный адрес ячейки А7, который не будет меняться при копировании формул. Примеры смешанной адресации: $B4 ‑ столбец В меняться не будет, а номер строки меняться будет. В таблице 3 приведены правила обновления ссылок при автозаполнении вдоль строки или вдоль столбца.

Таблица 2. Правила обновления ссылок при автозаполнении

Ссылка в исходной ячейке	Ссылка в следующей ячейке
	При заполнении вправо	При заполнении вниз
А1(относительная)	В1	А2
$А1 (абсолютная по столбцу)	$А1	$A2
А$1 (абсолютная по строке)	B$1	А$1
$А$1 (абсолютная)	$А$1	$А$1

Задание 1. Протабулировать функции у1 = х² и y2 = a·cos(x) на отрезке [‑5; 5] с шагом h = 1, если а = 5,35 . Построить графики функций у1 и у2.

Разобьем отрезок [-5; 5] точками с шагом h = 1, получим значения x₁ = -5, x₂ =-4, ... , x₁₁ =5.

Вычисление значений функции при значениях аргумента, взятых с некоторым шагом, принято называть табулированием функции.

Заполнить таблицу исходных данных (рис.9) - ячейки С4:С6; Е5.

Заполнить столбец А. Помните, что для автозаполнения номеров достаточно ввести лишь два первых значения, выделить их и растянуть.

Для заполнения столбца аргументов х установите в ячейку В9 ссылку на ячейку С5 (рис.10), где содержится значение начала отрезка табулирования.

В ячейке B10 вычисляется следующее значение аргумента как предыдущее значение плюс шаг. Для того чтобы адрес ячейки С6, содержащей значение шага h , при распространении формулы вниз не менялся, использована абсолютная адресация С$6 по строке.

В столбцах С и D вычисляются значения функций у1 и у2 при соответствующих значениях аргумента. В формуле для расчета у2 ссылка на значение константы а также имеет абсолютную адресацию (рис.10).

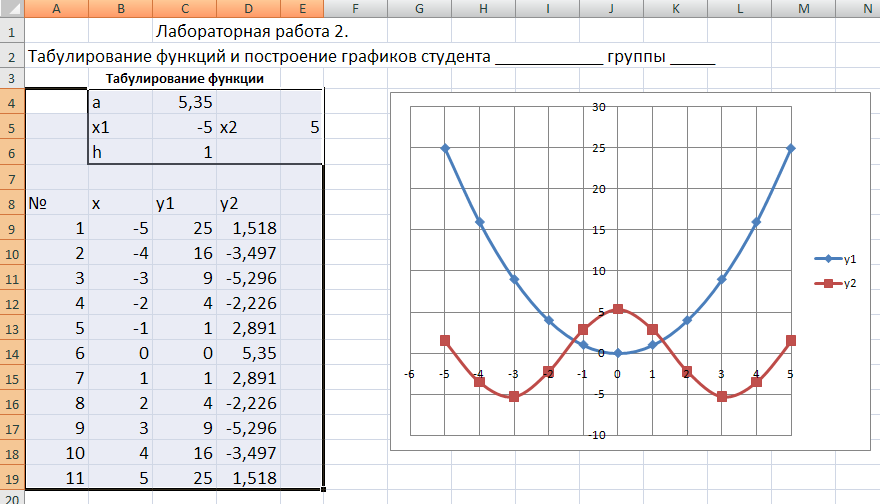
Рис.9. Таблица значений и графики функций у1 = х² и y2 = a*cos(x)

Рис.10. Формулы Excel, используемые для табулирования функций у1 = х² и у2 = а*cos(х)

Затем формулы строки 10 с помощью маркера заполнения распространяются вниз до строки 19.

Для построения графиков выделяется диапазон исходных данных (х, y1, y2), включая заголовки столбцов. Графики функций строятся по точкам, поэтому выбирается точечный тип диаграммы ВставкаТочечная.

Для редактирования значений по оси 0х, следует выделить ось и, нажав правую кнопку, выбрать команду Формат осиПараметры оси, задать максимальное и минимальное значения и цену основных делений по оси 0х.

В столбце Е вычислить значения функции у3 =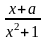 . При формировании формулы числитель и знаменатель необходимо взять в скобки.

Для добавления графика функции у3 в диаграмму достаточно щелкнуть график и на появившемся меню Конструктор вызвать Выбрать данные Диапазон данных для диаграммы. Выделить диапазон значений исходных данных (х, y1, y2, y3) и на графике получить третью кривую.

Функция ЕСЛИ. Логические операции используются в том случае, когда значение ячейки необходимо вычислять одним из нескольких способов, в зависимости от выполнения или невыполнения одного или нескольких условий. В ячейку записывается условие в виде функции логического ветвления (ЕСЛИ), которая имеет следующую структуру;

= ЕСЛИ (логич. выраж.; формула1; формула2).

Функция имеет три apгyмента:

Логич. выражение ‑ это любое значение или выражение, принимающие значения ИСТИНА или ЛОЖЬ. Например, А5=37 ‑ это логическое выражение, принимающее значение ИСТИНА, если в ячейке А5 находится число, равное 37, в противном случае функция принимает значение ЛОЖЬ.

Формула1 ‑ действие, которое будет выполняться, если условие принимает значение ИСТИНА.

Формула2 ‑ действие, которое будет выполняться, если условие принимает значение равно ЛОЖЬ.

Логическая функция ЕСЛИ позволяет вывести в ячейку одно из двух значений в зависимости от выполнения некоторого логического выражения.

Например, чтобы разместить в ячейке С12 максимальное из двух значений, содержащихся в ячейках С10 и С11, достаточно ввести в ячейку С12 формулу:

= ЕСЛИ(С10>С11;С10;С11)

Часто приходится использовать сложные условия и вложенные логические функции, например: в ячейке A1 содержится дата выполнения расчета. Требуется в заголовке рабочей таблицы (напри­мер, в ячейке В4) указать номер квартала. Очевидно, что номер квартала определяется в зависимости от месяца, а для выполнения поставленной задачи потребуется формула:

-ЕСЛИ(И(А1>-1; АК=3); "1-й квартал"; ЕСЛИ<И<(А1>3; А1<=6); "2-й квартал"; ЕСЛИ<И<А1>6; АК=9); "3-й квартал">;"4-й квартал⁴)»

Задание 2.

Задан объем продаж по каждому продавцу в течение недели. Требуется получить информацию о лучших продавцах, у которых средний объем продаж за неделю выше общего среднего значения.

Перейдите на новый лист. Для решения будем пользоваться стандартными функциями из Мастера функций ( ). Найдем среднее значение продаж в ячейке В15 с использованием функции СРЗНАЧ, найдем средние значения каждого продавца, которые разместим в ячейках С11 ‑ Н11 (рис.11).

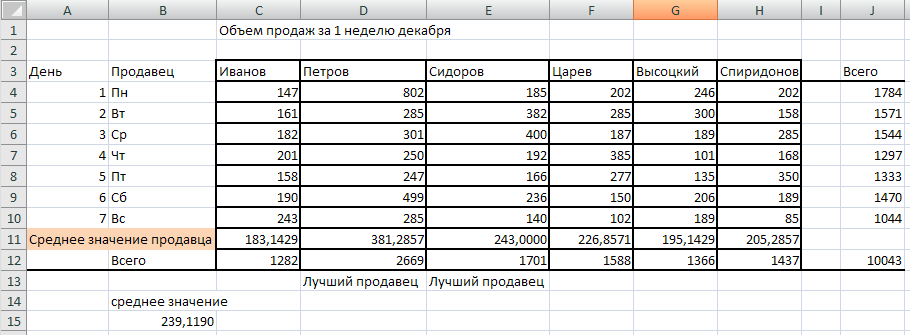
Рис.11. Рабочий лист с исходными данными и промежуточными вычислениями

Затем вызываем функцию ЕСЛИ и записываем ее в ячейку С13. Функция имеет три поля аргументов: логическое выражение; значение, если это выражение истинно; значение, если оно ложно. Запишем в поле логическое выражение ‑ C11>=$B$15, в поле значение_если_истина ‑ "Лучший продавец", поле значение_если_ложь – " ", т.е. в ячейке С13 окажется выражение «ЕСЛИ(С11>=$В$15;"Лучший продавец"; " ") (рис.12). Таблица с результатами расчетов представлена на рис.13.

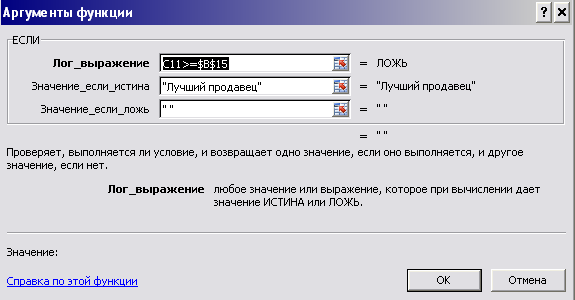
Рис.12. Окно Мастера функции для функции ЕСЛИ

Рис.13. Рабочий лист с результатами расчетов

Задание 3.

Протабулировать функции ,

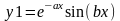на отрезке с шагом , если а = 1,5 и b = 8. Построить графики.

Реализация данного задания показана на рис.9-10. Обратите внимание на то, что в столбце Е использована функция ЕСЛИ для вывода надписи «end» при достижении конца отрезка табулирования.

Скопируйте лист с заданием 1. Для этого подведите курсор мыши () к имени листа и, удерживая Ctrl и нажатую левую клавишу мыши, оттащите в сторону. Появится новый лист с тем же именем и (2). Можете изменить имя нового листа. На этом листе вводим изменения в соответствии с условиями нового задания.

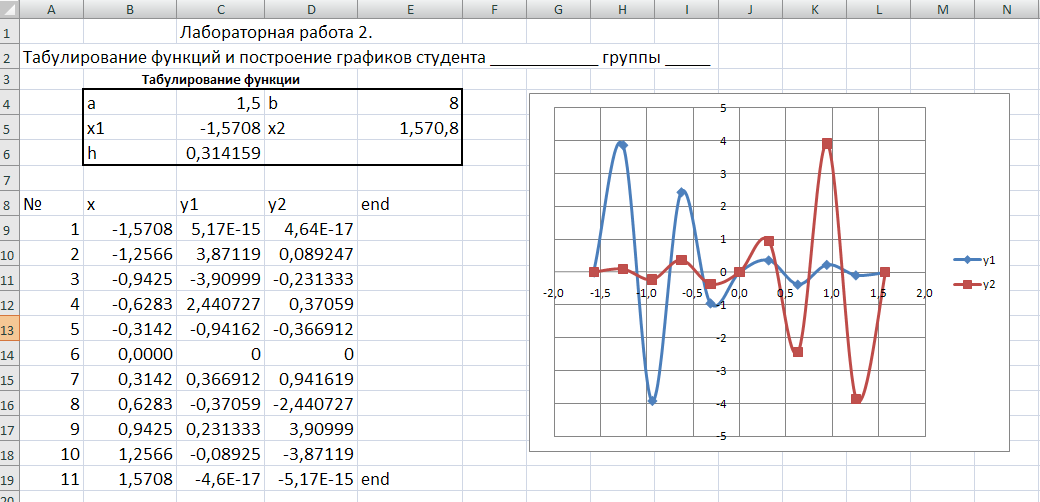
Рис.14. Таблица значений функций и

Рис.15. Формулы расчета (вторая строка этой таблицы распространяется вниз до появления слова «end»)

Рис.16. Графики функций и

Задание 4.

Протабулировать функцию на отрезке с шагом , если а = 1 и b = 7. Построить график.

Реализация данного задания показана на рис.17 ‑ 19. Обратите внимание на то, что в столбце С использована функция ЕСЛИ для вычисления значения функции. В частности, если условие выполняется, вычисление ведется по формуле y1=e^-axsin(bx), в противном случае используется формула у2 = b(1 - x²). Для простоты протабулируем как первую, так и вторую функции по всему отрезку (столбцы D и Е), и в функции ЕСЛИ приравняем у к первой функции при х<=0 и ко второй при х>0.

Рис.17. Формулы расчета (вторая строка этой таблицы распространяется вниз до появления слова «end»)

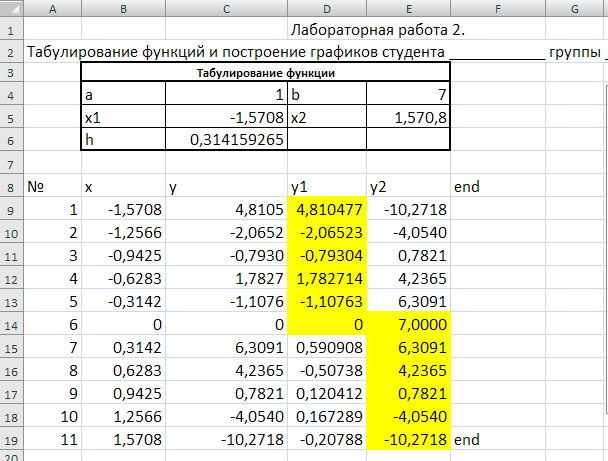
Рис.18. Таблица значений ветвящейся функции у(х)

Для построения графика функции с разрывом в виде скачка, представленного на рис.19, используется следующая процедура.

Рис.19. График ветвящейся функции у(х)

Для создания диаграммы сначала выделяется диапазон исходных данных с заголовками. В нашем случае выделяются ряды значений аргумента (В8:В14) и, удерживая клавишу Ctrl, значения функции до точки разрыва включительно (D9:D14), и во вкладке Вставка выбирается тип диаграммы Точечная. Получаем первую половину графика. Чтобы добавить вторую половину необходимо выделить график, щелкнув по нему, и в меню Конструктор выбрать Выбрать данные (рис.20). Для добавления нового графика выбираем Добавить и в появившемся окне (рис.21) в Значения Х вводим значения аргумента, начиная с точки разрыва, (В14:В19), и в Значения Y - значения функции (Е14:Е19) для второго графика.

Рис.20. Диалоговое окно Выбора данных

Рис.21. Диалоговое окно Добавления ряда данных

Задание 5.

Сделать копию листа с заданием 4. Ввести данные своего варианта в ячейки В4:Е6 (рис.16) из таблицы 1 приложения. Заполнить формулами ячейки С9, D9, Е9. Введенные формулы распространить вниз копированием. Построить графики функций своего варианта в одной системе координат, как это было сделано в задании 4, затем построить отдельные графики для первой и второй функций своего варианта.

Задание 6.

Составить отчет о выполнении индивидуального варианта в текстовом редакторе Microsoft Word.

Переписать формулировку задания 4, подставив свои исходные данные. Скопировать в Microsoft Word таблицу значений функции и график.