9. Дифференциальное ур-е равновесия ж-ти (вывод).

Рассм. покоящуюся однородную несжимаемую жидкость. Ж.ч. рассм. в виде прямоуг-го парал-да. В соотв. С моделью ж.в основе которой лежит гипотеза сплошности. Ж. можно представитьв виде бесконечной совокупности Ж. ч. К частицам применим законы механики твердого тела. Поэтому Д.у.равновесия ж.могут быть получены из условия рановесия поверхностных и массовых сил действующих на параллелепипед. Рассм. одну пространственную координату, например х. Выразим давление на левой и правой грани через Р в точке А. ) ) - частная производная, характеризующая интенсивность изменения давления вдоль оси х, при неизменных значениях y и z, соотв-х центрам рассм-х граней. Приращение Р при изменении координаты х на +- отн. точки А. Элементарные силы давления на грани равны - d )dy,dz d ) dy,dz (1)

Кроме элем-х поверхностных сил на объем действует массовая сила, равнод-я в т.А

d d d

)dydz- )dydz+

Раскроем скобки и полученный результат поделим на dx,dy,dz.

-дифуры равновесия жидкости.

Из уравнений Эйлера (1755г) следует, что изменение Р вдоль коор-ты x,y,z происходит за счет соответствующих изменений проекции и единичной массовой силы х, у,z. dP=ρ(xdx+ydy+zdz)

10. Давление в произвольной точке жидкости. Гидростатический закон распределения давления.

Дифференциальные уравнение равновесия жидкости (3) (4) (5) Умножим эти ур-я на dx dy dz и сложив их получаем

Где левая часть – полный дифференциал давления P=P(x,y,z)

(6)Соотношение (6) позволяет определить давление в любой точке покоящейся жидкости при произвольном направлении массовой силы.Гидростатический закон распределения давления.Рассмотрим покоящуюся жидкость находящуюся в поле сил тяжести.

Х=0, Y=0, z=-g подставим в (6)

Согласно закону для любой точки покоящейся однородной жидкости в пределах занимаемого объема, сумма есть величина постоянная. Основное уравнение гидростатики Выберем 2 произвольные точки на свободной поверхности

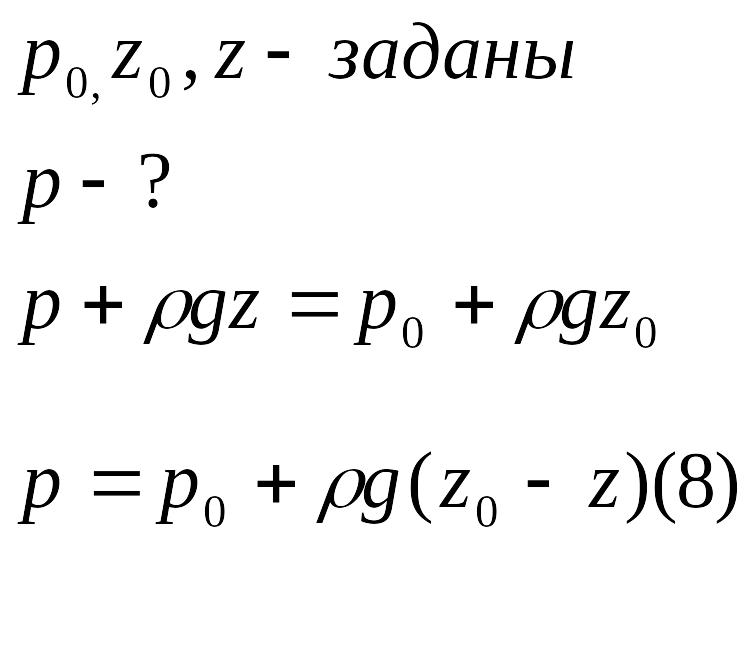(8) – основное уравнение гидростатики.

Каково бы ни было удаление поверхности сравнения, разности координат -z всегда равно глубине h.

(9)Анализ основного уравнения гидростатики (9) позволяет установить следующее

-Гидростатическое давление является линейной функцией глубины h и не зависит от размера и формы сосуда.-Давление в любой точке покоящейся жидкости складывается из давления на свободной поверхности p0 и давления pgh обусловленного весом вышележащих слоев жидкости.

11. Основное уравнение гидростатики.Выберем 2 произвольные точки на свободной поверхности

(8) – основное уравнение гидростатики.Каково бы ни было удаление поверхности сравнения, разности координат -z всегда равно глубине h. (9) Анализ основного уравнения гидростатики (9) позволяет установить следующее -Гидростатическое давление является линейной функцией глубины h и не зависит от размера и формы сосуда.-Давление в любой точке покоящейся жидкости складывается из давления на свободной поверхности p0 и давления pgh обусловленного весом выше лежащих слоев жидкости.