§8. Классическая теория теплоемкости газов

1.  Теорема о равномерном распределении энергии по степеням свободы.  Классическая теория теплоемкости газов основана на предположении, что к атомно-молекулярным системам применимы законы классической ньютоновой механики.  Ее центральным положением является сформулированный Больцманом постулат равномерного распределения механической энергии молекул по степеням свободы:

Если система молекул находится в тепловом равновесии при температуре T, то средняя механическая энергия равномерно распределена по всем степеням свободы и для каждой степени свободы каждой молекулы она равна ¹/₂kT.  Если всего степеней свободы i, то средняя кинетическая энергия каждой молекулы составляет ⁱ/₂kT.

2.  Теплоемкость одноатомных газов.  К идее постулата Больцмана можно прийти из анализа теплоемкости одноатомных газов.  Как было получено ранее согласно формуле (7.11), средняя кинетическая энергия молекул идеального газа составляет .

Полагая молекулы одноатомного газа по-прежнему материальными точками, мы можем приписать им по 3 степени свободы.  Тогда выходит, что на каждую степень свободы приходится в среднем энергия .  Внутренняя энергия одноатомного идеального газа . (8.1)

Изохорная молярная теплоемкость C_v . (8.2)

Изобарная молярная теплоемкость C_p = C_v . (8.3)

Показатель адиабаты (8.4)

Таблица 1
Газ			γ	Согласие с теорией
Гелий He	12,74	21,20	1,664	Хор.
Неон Ne	12,51	20,94	1,674	Хор.
Аргон Ar	12,86	20,89	1,625	Хор.
Криптон Kr	12,65	21,03	1,662	Хор.
Ксенон Xe	12,60	20,88	1,657	Хор.

В таблице 1 приведены опытные значения молярных теплоемкостей C_v, C_p и показателя адиабаты γ одноатомных газов при нормальном атмосферном давлении и при температуре 293 K. Классическая теория теплоемкости хорошо прогнозирует теплоемкость инертных газов. Максимальное расхождение, наблюдающееся у аргона, не превышает 3%.  

Хорошее соответствие с опытом наблюдается и в парах металлов.

3 .  Теплоемкость двухатомных газов.  Применительно к двухатомным молекулам несколько изменим критерий идеальности. При не очень больших скоростях движения двухатомные молекулы можно моделировать жесткими гантелеподобными стержнями. Атомы по-прежнему считаем материальными точками, находящимися на концах жесткого невесомого стержня, длина которого равна расстоянию между центрами масс атомов.  К трём степеням свободы поступательного движения таких молекул добавляются две степени вращательного (рис.20). Всего степеней свободы . Тогда , (8.5)

, (8.6)

. (8.7)

В таблице 2 приведены опытные значения молярных теплоемкостей C_v, C_p и показателя адиабаты γ двухатомных газов при нормальных условиях.

Таблица 2
Газ			γ	Согласие с теорией
Водород H2	20,42	28,76	1,408	Хор.
Азот N2	20,86	29,44	1,410	Хор.
Кислород O2	20,90	29,21	1,398	Хор.
Хлор Cl2	25,24	36,87	1,461	?
Оксид азота NO	20,85	29,28	1,404	Хор.
Оксид углер. CO	21,11	29,32	1,389	Хор.

Из таблицы видно, что двухатомные газы в целом удовлетворительно описываются построенной моделью теплоемкости. Непонятно лишь положение с хлором. Можно допустить, что в молекуле хлора вдоль оси появляются колебательные степени свободы.  В этом случае теорию надо уточнять.

4 .  Теплоемкость многоатомных газов.  Многоатомными считаются молекулы с числом атомов 3 и более. Благодаря тому, что валентные связи атомов образуют углы, отличные от 180˚, атомы в молекулах газов не располагаются вдоль одной прямой. Поэтому такие молекулы можно рассматривать как систему материальных точек, жестко связанных между собой и образующих пространственную фигуру. При не очень больших скоростях движения эти фигуры можно моделировать абсолютно твердыми телами с 6 степенями свободы (рис.21). Кроме 3 степеней свободы поступательного движения молекула имеет три степени вращательного движения. Тогда , (8.8)

, (8.9)

Таблица 3
Газ			γ	Согласие с теорией
Аммиак NH3	28,48	38,15	1,339	Удовлет.
Ацетилен C2H2	35,15	43,76	1,245	Плохое
Метан CH4	27,20	39,73	1,460	Удовлет.
Оксид углер.  CO2	28,73	36,83	1,282	Удовлет.
Пропан C3H8	72,60	81,97	1,129	Плохое
Этан C2H6	43,32	51,87	1,197	Плохое
Этилен C2H4	34,22	42,78	1,250	Плохое
Сероводород H2S	27,42	34,99	1,276	Удовлет.

. (8.10)

Из опытных значений таблицы 3 видно, что многоатомные газы описываются построенной моделью теплоемкости значительно хуже. Удовлетворительным можно считать согласие лишь у аммиака, метана, углекислого газа и сероводорода.  

5.  Уточнение классической теории теплоемкости. Как видно из таблиц 1, 2, 3, полное согласие теории с опытом наблюдается лишь в случае одноатомных газов. У двухатомных (хлор) и многоатомных (пропан, этан) наблюдаются существенные расхождения. Можно предположить, что у некоторых газов даже при комнатной температуре энергия поступательного движения молекул соизмерима с энергией связи между атомами.  В результате соударений атомы в молекуле начинают колебаться вдоль этой связи. Если колебания гармонические, то их появление должно приводить к увеличению числа степеней свободы на 2, то есть одна степень свободы соответствует средней кинетической энергии колебания , а другая степень свободы соответствует средней потенциальной энергии .

Полное число степеней свободы становится равным i = 6 + 2 = 8 у многоатомных газов и i = 5 + 2 = 7 у двухатомных газов.

Однако ситуация с хлором не исправляется.  При i = 7 C_V должно быть 7R/2 = 29,08 Дж(мольК) вместо 25,24 Дж/(мольК) на опыте, γ должно быть 97 = 1,285 вместо 1,461 на опыте.

Предложенное уточнение спасает положение у этилена.  Если положить i = 6 + 2 = 8, то C_V = 4R = 33,24 Дж(мольК) (34,22 на опыте),  = 108 = 1,250 (1,250 на опыте).  Близко к этой схеме подходит еще ацетилен.

У более сложных молекул число степеней свободы может быть еще более значительным.  Его можно находить из общей формулы (8.7).

. (8.11)

Для пропана, например, . Это значит, что у молекулы пропана кроме 6 пространственных степеней свободы должно быть еще 10 колебательных степеней. Колебательное движение должно происходить вдоль 5 связей.  Поскольку в молекуле пропана CH₃  CH₂  CH₃ всего две углерод-углеродных связи, то три колебательных связи должны быть углерод-водородные.  Но не ясен принцип отбора, ведь 6 атомов водорода находятся в одинаковом состоянии.

То, что для многих газов i – не целое число (метан, хлор, углекислый газ), означает, что предложенная модель не в состоянии учесть строго ту энергию, которая связана с внутренним движением в молекуле. Как показывает опыт, теплоемкость газов зависит и от температуры, тогда как в формулы для C_V и C_p температура T не входит.

Все это говорит о том, что классический принцип равномерного распределения энергии по степеням свободы не является универсальным.

6.  Границы применимости классической теории теплоемкости. Несмотря на многочисленные расхождения с опытом в случаях с многоатомными газами, классическая теория теплоемкости имеет очень важное достоинство: она чрезвычайно проста и наглядна. Она, безусловно, применима к одноатомным и с незначительными ограничениями к двухатомным газам. Для использования ее нужно знать лишь температурные границы применимости.

Н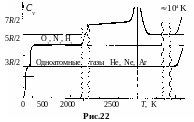 а рис.22 показана опытная зависимость теплоемкости одно- и двухатомных газов в диапазоне температур от 0 до  10⁴ K.

Теплоемкость одноатомных газов при T > 50 K полностью описывается построенной теорией.  Классическая модель справедлива вплоть до температур в десятки тысяч градусов, при которых начинается термическая ионизация атомов.

Для двухатомных газов классическая теория теплоемкости справедлива в области температур от 100 до 500 K.  Здесь C_V почти не зависит от температуры и для большинства газов близка к 5R2.  В интервале от 500 до 2500 K теплоемкость медленно растет и при T  2500 K обращается в бесконечность.  При этой температуре наступает диссоциация двухатомных молекул на отдельные атомы.  Подводимое к газу тепло расходуется на совершение работы по разрыву межатомных связей.

После диссоциации число частиц газа удваивается.  Молярная теплоемкость двухатомного газа при T от 2500 K до  10⁴ K переходит в молярную теплоемкость одноатомного газа с удвоенным числом частиц, .

Как для одноатомных, так и для двухатомных газов резкие расхождения классической теории с опытом наблюдаются в области низких температур.  У двухатомных газов при температурах  100 K теплоемкость падает с 5R2 до 3R2, то есть становится равной теплоемкости одноатомных газов.  Это можно объяснить лишь тем, что у двухатомных молекул «вымерзают» вращательные степени свободы, в результате двухатомная молекула, как и одноатомная, движется только поступательно.  

При температурах T ≤ 50 K теплоемкость всех газов с понижением температуры быстро убывает и при T → 0 стремится к нулю.

Эти расхождения теории с опытом можно объяснить лишь тем, что классическая теория теплоемкости не совершенна.  Более верная теория может быть построена на основе квантовых представлений, основанных на идее дискретного изменения энергии атомно-молекулярных объектов.