Глава 5. Твердые тела §20. Кристаллическая структура твердых тел

1.  Кристаллические и аморфные тела. Твердые тела сохраняют объем и форму. По своей внутренней структуре они делятся на кристаллические и аморфные. Тела с регулярным расположением атомов или молекул, называют кристаллическими. В кристаллах существует дальний порядок.

В аморфных телах молекулы расположены примерно так же, как и в жидкостях. В этом смысле аморфные тела называют переохлажденными жидкостями. В них существует ближний порядок.

Свойства кристаллических тел определяются не только свойствами атомов и молекул, образующих кристалл, но также их расположением. Благодаря их регулярной структуре кристаллы анизотропны. Их физические свойства зависят еще и от направления в кристалле.

2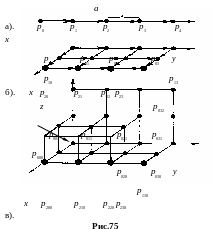 .  Трансляции. Как показал в 1848 г. француз Браве, прерывная периодическая структура кристалла с геометрической точки зрения может быть осуществлена параллельным переносом (трансляцией) определенной комбинации частиц. Различают одномерную, двумерную и трехмерную трансляцию.

1. Одномерная (линейная) трансляция. Положение точки p определяется вектором трансляции, 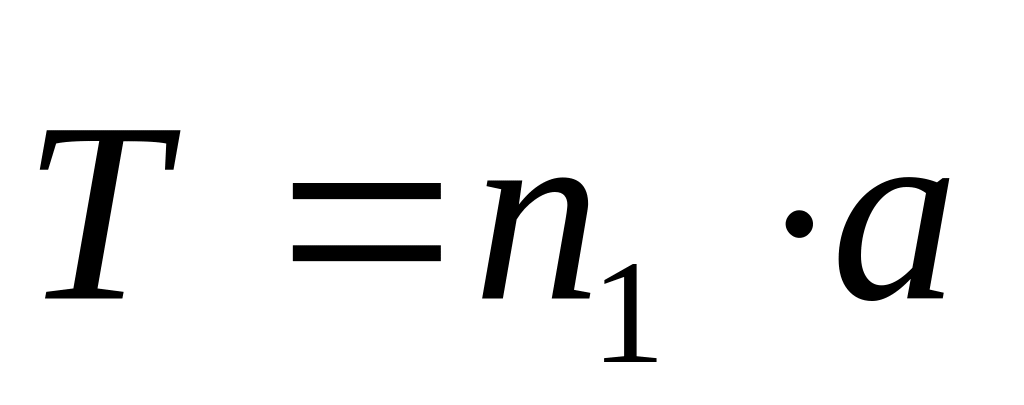, где a – период трансляции, n₁= 0, 1, 2 3, …– целое число (рис.75а).

б.   Двумерная (плоская) трансляция. Положение точки в этом случае определяется вектором трансляции , где a и b – периоды трансляции в соответствующих направлениях, а n₁ и n₂ – целые числа (рис.75-б).

в.   Трехмерная трансляция формирует пространственную решетку. Положение любой точки в ней определяется вектором трансляции (рис.75-в).

Применительно к реальным кристаллам точки p называются узлами кристаллической решетки.

3.  Решетка Браве. Комбинация из минимальных векторов , и , с помощью которой реализуется сколь угодно протяженный кристалл, называется базисом решетки. Параллелепипед с ребрами a, b, c называется основным (базисным) параллелепипедом или решеткой Браве. Вместе с атомами, которые в нем находятся, параллелепипед Браве (решетка Браве) образует элементарную ячейку кристалла. Весь кристалл может быть образован трансляцией таких ячеек.

Различают 4 типа решеток Браве. а. Простая (примитивная) – узлы расположены только в вершинах параллелепипеда. В среднем на решетку Браве приходится один атом; б. Базоцентрированная, добавляется еще по одному узлу в центрах двух противоположных граней. В среднем на решетку приходится 2 атома; в. Объемноцентрированная, к узлам в углах добавляется один узел в центре, средняя плотность упаковки 2 узла на решетку Браве; г. Гранецентрированная, к узлам в углах добавляются 6 атомов в центрах всех граней. Плотность упаковки 4 узла на решетку Браве.

4.  Симметрии. Это свойство тел совмещаться с самим собой при некоторых мысленных перемещениях, называемых операциями симметрии. К ним относятся параллельный перенос (трансляция), поворот тела вокруг оси, отражение в плоскости, отражение в точке. Различают следующие элементы симметрии:

1. П лоскость симметрии, когда любая точка одной половины кристалла совпадает с зеркальным отражением точки другой половины (рис.76-б).

б.   Поворотная ось симметрии. Если точки кристалла совмещаются с подобными им при повороте кристалла на определенный угол φ вокруг оси, то эта ось называется осью симметрии n-го порядка. В кристаллах реализуются случаи с n = 1, 2, 3, 4, 6 (рис.75-а).

в.   Зеркально-поворотная ось симметрии. Одна половина тела совмещается с зеркальным отражением другой половины лишь после поворота на некоторый угол (рис.76-в).

г.   Центр симметрии. Если в теле существует точка, обладающая свойством, что при замене радиуса-вектора на обратный тело переходит в состояние, неотличимое от исходного, то эта точка называется центром симметрии (рис.76-г). В шаре, цилиндре, эллипсоиде, кубе геометрический центр есть центр симметрии.

Р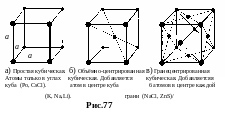 ешетки Браве кристаллов могут иметь следующие элементы симметрии: центр симметрии, поворотные и зеркально поворотные оси симметрии 1, 2, 3, 4, 6 порядков, плоскость симметрии.

5.  Системы кристаллов. Их 7. Деление кристаллов на системы производится по числу поворотных осей симметрии различных порядков, которыми обладает решетка Браве. Системы характеризуются периодами трансляции a, b, c и углами между сторонами параллелепипеда Браве α, β, γ.

1. Кубическая система. Параллелепипед Браве – куб. Различают 3 типа решеток Браве кубической системы: простая кубическая (рис.77-а), объемноцентрированная кубическая (рис.77-б), гранецентрированная кубическая (рис.77-в). В решетках кубической системы а = b = c,  =  =  =90°.

П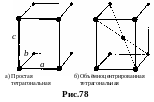 араметр a в решетках кубической системы называют постоянной решетки. В металлах а  10^10 м. В простом кубе приходится в среднем 1 атом на элементарную ячейку, в объемноцентрированном – 2 атома, в гранецентрированном – 4 атома. Последний тип упакован более плотно.

б.   Тетрагональная система. Решетка Браве – прямая квадратная призма. Существует два типа – простая и объемноцентрированная (рис.78). а = b  c,  =  =  =90°.

в.   Гексагональная система. Минимальный структурный элемент кристалла, передающий все виды симметрии, есть правильная шестигранная призма, в центрах оснований которой имеется по одному атому (рис.79). Эту призму можно представить как комбинацию из трех примитивных решеток Браве – призм, в основании которых ромб с острым углом 60°. Система имеет один тип. а = b  c,  = 60°,  =  =90°.

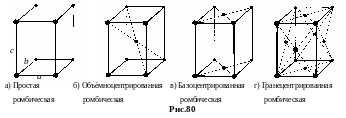г.   Ромбическая (ортогональная) система. Решетка Браве – прямоугольник с тремя различными длинами ребер а  b  c,  =  =  =90°. Реализуются все 4 типа решетки Браве (рис.80).

д.   Моноклинная система. Решетка Браве есть прямая призма, в основании которой лежит произвольный параллелограмм. а  b  c,   90°,  =  =90°. Существует два типа решетки Браве моноклинной системы – простая (рис.81-а) и базоцентрированная (рис. 81-б).

е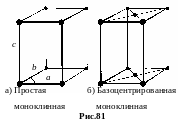 .   Триклинная система. Решетка браве представляет собой параллелепипед произвольной формы. а  b  c,     . Существует только один тип простой решетки (рис.82).

ж.   Ромбоэдрическая система. Решетка Браве – ромбоэдр, то есть сжатый в направлении пространственной диагонали куб. Все грани ромбоэдра одинаковые ромбы. а = b = c,  =  =  90°. Решетка Браве простая (рис.83).

В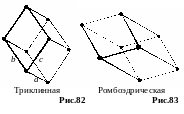 се 14 типов решеток Браве нашел только геометрически и трактовал их как возможные. Опыт показал, что все они реализуются в природе.

6.  Физические типы кристаллов. По характеру химических связей между узлами различают 4 типа кристаллов: ионные, атомные, металлические и молекулярные.

1. Ионные кристаллы. В соседних узлах ионы противоположного знака, а весь монокристалл фактически есть одна гигантская молекула.

К ионным кристаллам относятся соли 1 и 7 групп таблицы Менделеева: NaCl, CsCl, CsF, LiCl и т.д., а также некоторые интерметаллические соединения: AuZn, MgAg, CdAg.

Н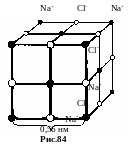 а рис.84 показана решетка Браве поваренной соли NaCl. Постоянная решетки a = 0,56 нм. Решетка относится к типу кубической гранецентрированной системы.

б.   Атомные кристаллы. В узлах - нейтральные атомы с ковалентной связью между собой. Суть ее в коллективизации валентных электронов. Примером атомного кристалла является алмаз. Атомы углерода в нем удерживаются ковалентной связью. Решетку алмаза можно представить как две гранецентрированные кубические решетки, вставленные одна в другую и смещенные относительно друг друга вдоль пространственной диагонали куба на четверть ее длины. Постоянная решетки алмаза a = 0,36 нм.

в.   Металлические кристаллы. В узлах - ионы одного положительного знака, между ними – слабо связанные с ионами отрицательные электроны, способные перемещаться в кристалле за счет энергии теплового движения. Это электроны проводимости, иначе, электронный газ. Обычно это металлы. Монокристаллы металлов бывают очень редко. Чаще поликристаллы, хаотично ориентированные в пространстве. Например, Li, a = 0,35 нм, Al, a = 0,4 нм, Fe, a = 0,29 нм, Cu, a = 0,36 нм.

г.   Молекулярные кристаллы. В узлах - определенным образом ориентированные молекулы, связанные между собой силами Ван дер Ваальса. Например, лед H₂O, твердая углекислота CO₂, твердые газы H₂. N₂, O₂.

Силы Ван дер Ваальса действуют также в кристалле графита. Графит – единственный элемент с гексагональной решеткой (рис.79). В плоскости слоев, где a = 0,25 нм, действует ковалентная связь, а между слоями (c = 0,67 нм) – силы Ван дер Ваальса. Четвертый валентный электрон в каждом атоме углерода остается свободным, поэтому добавляется еще металлическая связь. Графит имеет слоистую структуру и проводит электрический ток.

7.  Дефекты в кристаллах. Это отступления в реальных кристаллах от строго регулярной структуры. Отметим следующие дефекты:

1. Точечные. К ним относятся вакансии (отсутствие атома в каком либо узле решетки), примесные дефекты (замена «своего» атома решетки каким-либо другим «чужим» атомом), межузельные атомы (внедрение своего или чужого атома в межузельное пространство). Пара, состоящая из межузельного иона и оставленной им вакансии, называется дефектом Френкеля.

Все точечные дефекты, за исключением примесных, имеют кинетическую природу и термодинамически равновесны. При нагревании кристалла концентрация вакансий и межузельных атомов возрастает экспоненциально;

б.   Линейные дефекты. В реальных кристаллах некоторые атомные плоскости могут обрываться. Края таких оборванных плоскостей образуют дефекты, называемые краевыми дислокациями. Подвижностью дислокаций объясняется пластичность металлов;

в.   Двумерные дефекты образуются границами электрических и магнитных доменов, границами разных фаз в сплавах (мартенситы в сталях);

г.   Объемные дефекты образуются скоплениями вакансий, примесей, пузырьками газов.

Дефекты в кристаллах существенно изменяют их физические свойства – предел прочности, предел пластичности, спектры поглощения, рассеивания, люминесценции, электро- теплопроводность, магнитные свойства.