
- •I. Элементы линейной и векторной алгебры, аналитической геометрии.
- •1. Определители второго и третьего порядков. Основные свойства. Минор и алгебраическое дополнение. Понятие определителя n-ого порядка и его вычисление.
- •Свойства определителей.
- •2. Матрицы, действия над матрицами. Обратная матрица. Ранг матрицы.
- •Основные действия над матрицами.
- •Обратная матрица.
- •Свойства обратных матриц.
- •3. Системы линейных уравнений. Теорема Кронекера-Капелли (формулировка). Правило Крамера.
- •Элементарные преобразования систем.
- •Теорема Кронекера – Капелли. (условие совместности системы)
- •Метод Крамера.
- •4. Решение систем линейных уравнений матричным методом.
- •5. Метод Гаусса. Однородные системы линейных уравнений и их решение. Метод Гаусса.
- •Однородные системы линейных уравнений
- •6. Векторы. Линейные операции над векторами и их свойства.
- •Свойства векторов.
- •7. Проекция вектора на ось. Свойства проекций.
- •Некоторые свойства проекций
- •8. Линейная зависимость векторов. Разложение вектора по базису. Линейная зависимость векторов.
- •9. Декартова система координат. Координаты вектора. Система координат.
- •Декартова система координат.
- •Линейные операции над векторами в координатах.
- •10. Направляющие косинусы, длина вектора.
- •11. Деление отрезка в данном отношении.
- •12. Скалярное произведение векторов, его свойства, вычисление и применение.
- •13. Векторное произведение векторов, его свойства, вычисление и применение.
- •Свойства векторного произведения векторов:
- •14. Смешенное произведение векторов, его свойства, вычисление и применение.
- •Свойства смешанного произведения:
- •15. Прямая линия на плоскости. Различные способы задания. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой на плоскости. Уравнение линии на плоскости.
- •Уравнение прямой на плоскости.
- •Уравнение прямой по точке и вектору нормали.
- •Уравнение прямой по точке и направляющему вектору.
- •Параметрическое уравнение прямой
- •Уравнение прямой, проходящей через две точки.
- •2. Условие перпендикулярности.
- •16. Плоскость в пространстве. Различные способы задания. Взаимное расположение плоскостей. Расстояние от точки до плоскости. Общее уравнение плоскости.
- •Уравнение плоскости по точке и вектору нормали.
- •Уравнение плоскости в отрезках.
- •Уравнение плоскости, проходящей через три точки.
- •17. Прямая в пространстве. Различные способы задания. Взаимное расположение прямых в пространстве. Уравнение прямой в пространстве по точке и направляющему вектору.
- •Уравнение прямой в пространстве, проходящей через две точки.
- •Общие уравнения прямой в пространстве.
- •Условия параллельности и перпендикулярности прямых в пространстве.
- •Угол между прямыми в пространстве.
- •18. Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.
- •Условия параллельности и перпендикулярности прямой и плоскости в пространстве.
- •Эллипс.
- •Гипербола.
- •Парабола.
- •20. Поверхности второго порядка. Цилиндрические поверхности. Исследование поверхностей методом сечений. Поверхности второго порядка.
- •С фера:
- •К онус второго порядка:
- •Двуполостный гиперболоид:
- •Эллиптический параболоид:
- •Г иперболический параболоид:
- •II. Введение в математический анализ
- •21. Множество действительных чисел.
- •Операции над множествами.
- •22. Функция, область ее определения и способы задания. Сложные и обратные функции.
- •Способы задания функций
- •Сложная функция.
- •Обратная функция.
- •23. Свойства (четность, периодичность, монотонность, ограниченность) и графики функций.
- •24. Гиперболические функции, их свойства и графики.
- •25. Числовые последовательности. Предел числовой последовательности.
- •Ограниченные и неограниченные последовательности.
- •26. Число е. Натуральные логарифмы.
- •Связь натурального и десятичного логарифмов.
- •2 7. Предел функции в точке, односторонние пределы. Геометрическая иллюстрация определений.
- •28. Предел функции в бесконечности. Геометрическая иллюстрация.
- •29. Бесконечно малые функции и их свойства. Бесконечно большие функции. Связь между бесконечно малыми и бесконечно большими функциями.
- •Бесконечно большие функции и их связь с бесконечно малыми.
- •30. Основные теоремы о пределах.
- •Теорема доказана.
- •31. Первый и второй замечательные пределы.
- •32. Сравнение бесконечно малых функций.
- •33. Непрерывность функций в точке и на отрезке. Точки разрыва функции и их классификация.
- •Точки разрыва и их классификация.
- •Непрерывность функции на интервале и на отрезке.
- •34. Свойства функций непрерывных в точке.
- •Непрерывность некоторых элементарных функций.
- •35. Свойства функций непрерывных на отрезке (теоремы Вейерштрасса, Коши, о промежуточных значениях) и их геометрических смысл.
- •III. Дифференциальное исчисление функции одной переменной.
- •36. Задачи, приводящие к определению производной.
- •37. Производная функции, ее геометрический и механический смыслы.
- •38. Односторонние производные. Производная сложной и обратной функции. Односторонние производные функции в точке.
- •Производная сложной функции.
- •Производная обратных функций.
- •Основные правила дифференцирования.
- •Производные основных элементарных функций.
- •Дифференциал функции.
- •42. Свойства дифференциала и инвариантность его формулы. Применение дифференциала к приближенным вычислениям.
- •Применение дифференциала к приближенным вычислениям.
- •43. Производные и дифференциалы высших порядков. Производные и дифференциалы высших порядков.
- •Общие правила нахождения высших производных.
- •44. Основные теоремы дифференциального исчисления: Ролля (с доказательством), Коши (без доказательства), Лагранжа (с доказательством). Теорема Ролля
- •Теорема Коши.
- •Теорема Лагранжа.
- •45. Правило Лопиталя (доказательство для случая неопределенности ). Правило Лопиталя.
- •Точки экстремума.
- •Асимптоты.
- •Вертикальные асимптоты.
- •Наклонные асимптоты.
23. Свойства (четность, периодичность, монотонность, ограниченность) и графики функций.
1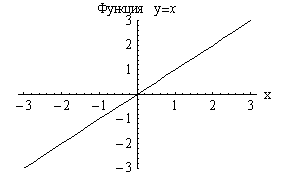
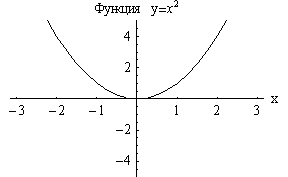 .
Функция
,
определенная на множестве
,
называется четной,
если
.
Функция
,
определенная на множестве
,
называется четной,
если
![]() выполняются условия
выполняются условия
![]() и
и
![]() нечетной,
если
выполняются условия
и
нечетной,
если
выполняются условия
и
![]() .
.
График
четной функции симметричен относительно
оси
![]() ,
а нечетной – относительно начала
координат.
,
а нечетной – относительно начала
координат.
Например,
![]() четные
функции; а
четные
функции; а
![]() нечетные функции;
нечетные функции;
![]() функции общего вида, т.е. не четные и не
нечетные.
функции общего вида, т.е. не четные и не
нечетные.
2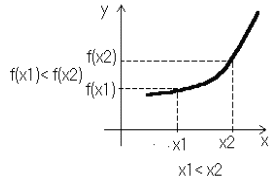
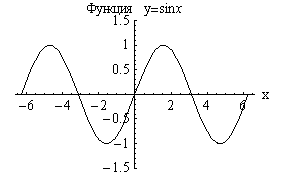 .
Функция
,
определенная на множестве
,
называется периодической
на этом множестве, если существует такое
число
.
Функция
,
определенная на множестве
,
называется периодической
на этом множестве, если существует такое
число
![]() ,
что при каждом
,
что при каждом
![]() значение
значение
![]() и
и
![]() При этом число
При этом число
![]() называется периодом
функции. Если
- период функции, то ее периодами будут
также числа
называется периодом
функции. Если
- период функции, то ее периодами будут
также числа
![]() ,
где
,
где
![]() Так, для
Так, для
![]() периодами будут числа
периодами будут числа
![]() Основной период (наименьший положительный)
– это период
Основной период (наименьший положительный)
– это период
![]() .
Вообще обычно за основной период берут
наименьшее положительное число
,
удовлетворяющее равенству
.
Вообще обычно за основной период берут
наименьшее положительное число
,
удовлетворяющее равенству
3.
Функция y=f(x)
называется возрастающей
на некотором интервале если для любых
х из этого интервала большему значению
аргумента соответствует большее значение
функции, т.е. при
![]() имеет место неравенство f(x1)<f(x2)
.
имеет место неравенство f(x1)<f(x2)
.
 Функция
y=f(x)
называется невозрастающей,
если на некотором интервале
имеет место неравенство f(x1)≥f(x2)
.
Функция
y=f(x)
называется невозрастающей,
если на некотором интервале
имеет место неравенство f(x1)≥f(x2)
.
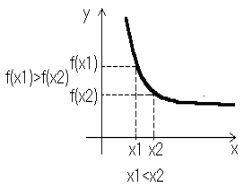
Функцияy=f(x) называется убывающей на некотором интервале, если для любых х из этого интервала большему значению аргумента соответствует меньшее значение функции, т.е. при имеет место неравенство f(x1)>f(x2) .
Функция y=f(x) называется неубывающей, если на некотором интервале имеет место неравенство f(x1)≤f(x2) .
Функции только убывающие или только возрастающие называются монотонными.
4.
Функцию
,
определенную на множестве
,
называют ограниченной
на этом множестве, если существует такое
число
![]() ,
что для всех
выполняется неравенство
,
что для всех
выполняется неравенство
![]() (короткая запись:
,
,
называется ограниченной на
,
если
(короткая запись:
,
,
называется ограниченной на
,
если
![]() ).
Отсюда следует, что график ограниченной
функции лежит между прямыми
).
Отсюда следует, что график ограниченной
функции лежит между прямыми
![]() и
и
![]() .
.
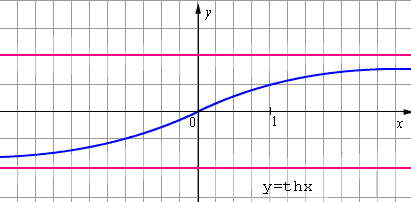
24. Гиперболические функции, их свойства и графики.
К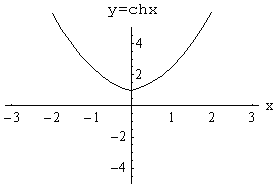 ним относятся:
ним относятся:
![]() -
гиперболический косинус
и
-
гиперболический косинус
и
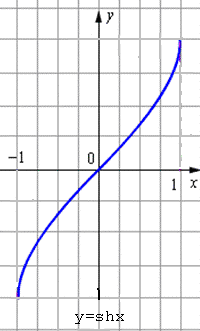
![]() -
гиперболический синус.
-
гиперболический синус.
С помощью этих функций можно определить еще 2 функции:
![]() -
гиперболический тангенс
и
-
гиперболический тангенс
и
![]()
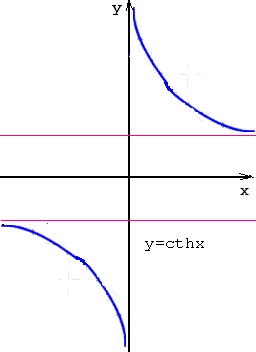 -
гиперболический котангенс.
-
гиперболический котангенс.
Функции
![]() определены, очевидно, для всех значений
.
Функция же
определены, очевидно, для всех значений
.
Функция же
![]() определена всюду, за исключением точки
определена всюду, за исключением точки
![]() .
.
Из
определения функций
![]() и
и
![]() следуют соотношения, аналогичные
соотношениям между соответствующими
тригонометрическими функциями:
следуют соотношения, аналогичные
соотношениям между соответствующими
тригонометрическими функциями:
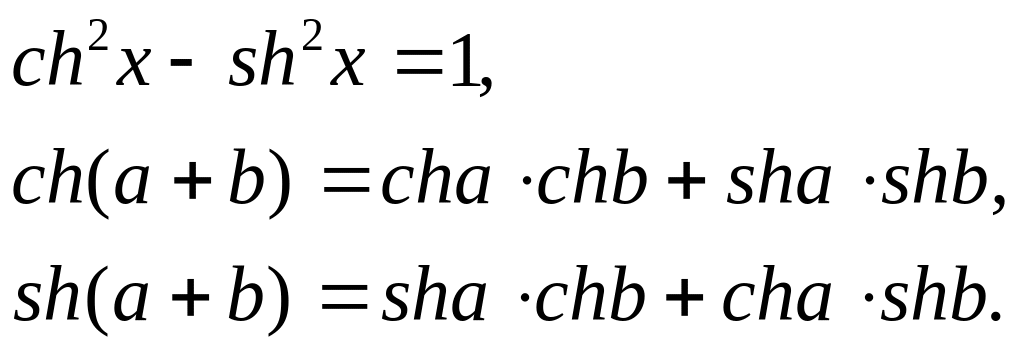
Название
"гиперболические функции" объясняется
тем, что функции
![]() и
и
![]() играют ту же роль для параметрического
представления гиперболы
играют ту же роль для параметрического
представления гиперболы
![]()
какую
тригонометрические функции
![]() и
и
![]() - для параметрического представления
окружности
- для параметрического представления
окружности
![]()
Производные гиперболических функций определяются формулами:
![]()
25. Числовые последовательности. Предел числовой последовательности.
Определение. Если каждому натуральному числу n поставлено в соответствие число хn, то говорят, что задана последовательность
x1, х2, …, хn = {xn}
Общий элемент последовательности является функцией от n.
xn = f(n)
Таким образом последовательность может рассматриваться как функция порядкового номера элемента.
Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.
Пример. {xn} = {(-1)n} или {xn} = -1; 1; -1; 1; …
{xn} = {sinn/2} или {xn} = 1; 0; 1; 0; …
Для последовательностей можно определить следующие операции:
Умножение последовательности на число m: m{xn} = {mxn}, т.е. mx1, mx2, …
Сложение (вычитание) последовательностей: {xn} {yn} = {xn yn}.
Произведение последовательностей: {xn}{yn} = {xnyn}.
Частное последовательностей:
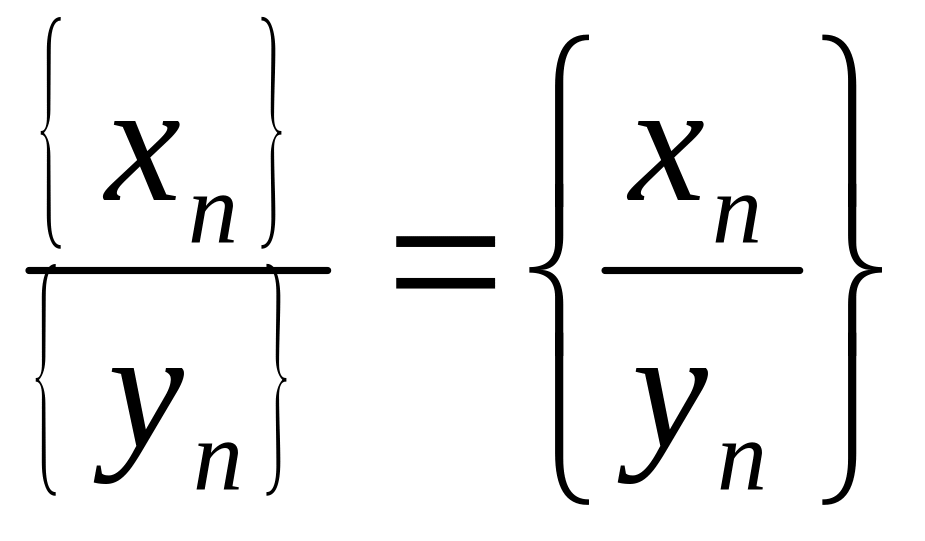 при
{yn}
0.
при
{yn}
0.
