
- •Вихревое электрическое поле
- •Вихревое электрическое поле
- •Свободные затухающие электрические колебания
- •Вынужденные электрические колебания
- •Резонанс напряжений и резонанс токов
- •Уравнение плоской электромагнитной волны
- •Энергия электромагнитных волн
- •Стоячая волна
- •Интерференция двух монохроматических волн
Уравнение плоской электромагнитной волны
![]()
При
прохождении монохроматической электромагнитной
волны частотой
ω векторы E и H в
данной фиксированной точке пространства
испытывают синфазные и только синфазные
гармонические колебания с этой же
частотой
![]() Из
условия синфазности следует, что в тех
точках пространства, где E
= 0 должно
быть и H
= 0,
аналогично и по амплитудным
значениям E0 и H0.
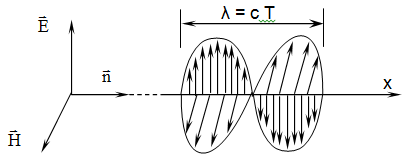
Это значит, что векторная волна
электрического поля E пространственно
совпадает с векторной волноймагнитного
поля H,
но только при этом векторы E и H колеблются
во взаимно – перпендикулярных плоскостях,
как это показано на рисунке ниже
Из
условия синфазности следует, что в тех
точках пространства, где E
= 0 должно
быть и H
= 0,
аналогично и по амплитудным
значениям E0 и H0.
Это значит, что векторная волна
электрического поля E пространственно
совпадает с векторной волноймагнитного
поля H,
но только при этом векторы E и H колеблются
во взаимно – перпендикулярных плоскостях,
как это показано на рисунке ниже
 Если
источником задается одно единственное
направление x для
излучения электромагнитной
волны,
то фронт волны будетплоским,
а волна одномерной, как для вектора E,
так и для вектора H.
В этом случае волну можно представить
двумя уравнениями, соответственно
Если
источником задается одно единственное
направление x для
излучения электромагнитной
волны,
то фронт волны будетплоским,
а волна одномерной, как для вектора E,
так и для вектора H.
В этом случае волну можно представить
двумя уравнениями, соответственно
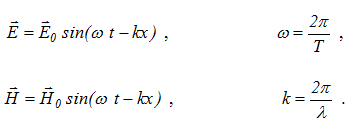
42
Энергия электромагнитных волн
Как показывает опыт, электромагнитные волны могут производить различные действия: нагревание тел при поглощении света, вырывание электронов с поверхности металла под действием света (фотоэффект). Это свидетельствует о том, что электромагнитные волны переносят энергию. Эта энергия заключена в распространяющихся в пространстве электрическом и магнитном полях.
В курсе электричества и магнетизма было показано, что объемная плотность энергии электрического поля равна
|
(1.1) |
а магнитного поля –
|
(1.2) |
где ![]() и
и ![]() –
электрическая и магнитная постоянные.
Таким образом, полная плотность энергии
электромагнитной волны равна
–
электрическая и магнитная постоянные.
Таким образом, полная плотность энергии
электромагнитной волны равна
|
(1.3) |
Так
как модули вектора напряженности
электрического и индукции магнитного
поля в электромагнитной волне связаны
соотношением ![]() ,
то полную энергию можно выразить только
через напряженность электрического
поля или индукцию магнитного поля:
,
то полную энергию можно выразить только
через напряженность электрического
поля или индукцию магнитного поля:
|
(1.4) |
Из (1.4) видно, что объемная плотность энергии складывается из двух равных по величине вкладов, соответствующих плотностям энергии электрического и магнитного полей. Это обусловлено тем, что в электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры».
Плотность энергии электромагнитного поля можно представить в виде:
|
(1.5) |
Формула (1.5) характеризует плотность энергии в любой момент времени в любой точке пространства.
Если
выделить площадку с площадью s,
ориентированную перпендикулярно
направлению распространения волны, то
за малое время Δtчерез
площадку пройдет энергия ![]() ,
равная
,
равная
![]() ,
,
где ![]() –
скорость электромагнитной волны в
вакууме.
–
скорость электромагнитной волны в
вакууме.
Плотностью потока энергии называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади, перпендикулярной к направлению распространения волны:
|
(1.6) |
Подставляя
в последнее соотношение выражения
для ![]() и
,
получим
и
,
получим
![]() .
.
Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергииэлектромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
![]() (в
системе СГС),
(в
системе СГС),
![]() (в
системе СИ),
(в
системе СИ),
где E и H — векторы напряжённости электрического и магнитного полей соответственно.
![]() (в
комплексной форме)[1],
(в
комплексной форме)[1],
где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно.
Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.
Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то вектор Sнепрерывен на границе двух сред.
[править]Вектор Пойнтинга и импульс электромагнитного поля
В силу симметричности тензора энергии-импульса, все три компоненты вектора пространственной плотности импульса электромагнитного поля равны соответствующим компонентам вектора Пойнтинга, делённым на квадрат скорости света:
![]() (в
системе СИ)
(в
системе СИ)
В этом соотношении проявляется материальность электромагнитного поля.
Поэтому, чтобы узнать импульс электромагнитного поля в той или иной области пространства, достаточно проинтегрировать вектор Пойнтинга по объёму.
[править]История
43

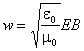 .
.