2.2. Дифференцируемость функции комплексного переменного. Условия Коши-Римана -

Эйлера- Даламбера аналитичности функции.

Дифференцируемость функции комплексного переменного.

Пусть однозначная функция w = f(z) определена в некоторой окрестности точки z, включая и саму точку. Тогда предел

если он существует, называется производной функции f(z) в точке z, а функция f(z) называется дифференцируемой в точке z.

Из дифференцируемости функции f(z) в некоторой точке z сле­дует ее непрерывность в этой точке (отношение при мо­жет стремиться к конечному пределу f(z) лишь при условии, что и ). Обратное утверждение не имеет места.

Теорема. Если функция w = и(х;у) + iv(x;y) определена в не­которой окрестности тонки z= х + iу, причем в этой точке действи­тельные функции и(х; у) и v(x; у) дифференцируемы, то для дифференцируемости функции w=f(z) в точке z необходимо и достаточно, чтобы в этой точке выполнялись равенства

,

Условия Коши-Римана -

Эйлера- Даламбера аналитичности функции.

2.3. Интеграл в комплексной области. Интегральные теоремы и формулы Коши.

Т: Если функция аналитична в односвязной замкнутой облости с границей , то (2)

Односвязная область- область, новые две точки которой можно соединить непрерывной линией, не выходя за эту область. Иначе, область многосвязна,

Док-во (Т):

(поскольку функция аналитическая и к ней применимо правило Коши- Римана).

Интегральная теорема Коши для многосвязной области.

Т: - аналитическая функция в многосвязной области с внешней границей и -границы замкнутых контуров внутри области , тогда

Док - во:

Приведем в случае трехсвязной области.

Сделаем 2 разреза. Путем их сводим нашу область к односвязной.

Для односвязной области справедлива интегральная теорема Коши

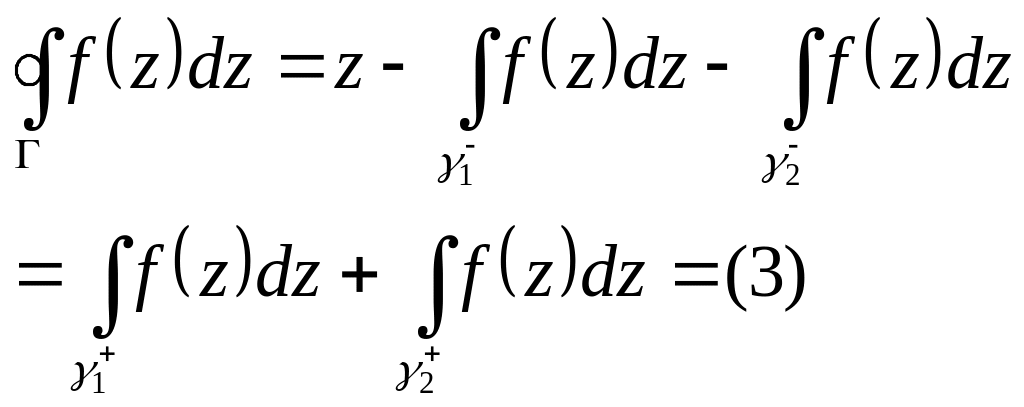
Если функция аналитическая, то интеграл от нее не зависит от пути интегрирования.

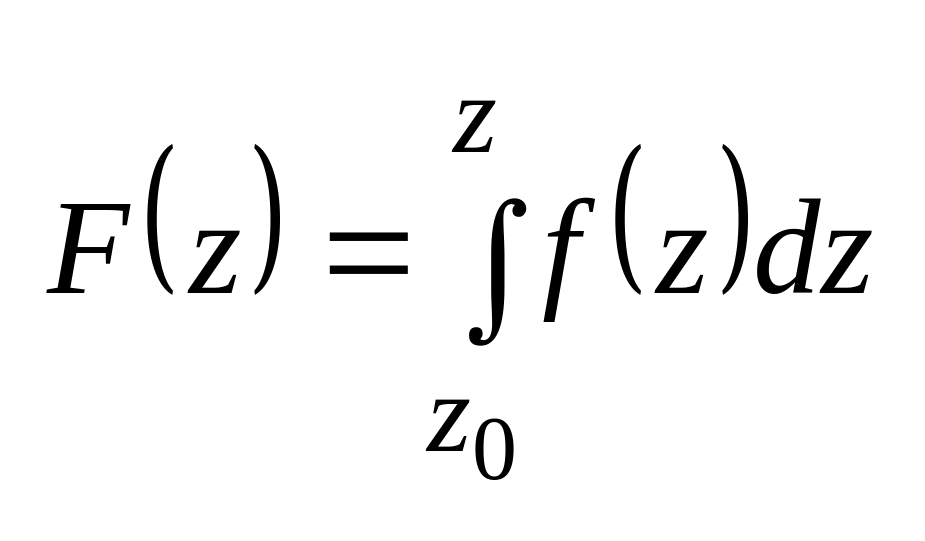
Если такова, что интеграл от нее не зависит от пути интегрирования, то явл. Аналитической и (теорема Мереры)

первообразная для функции

Если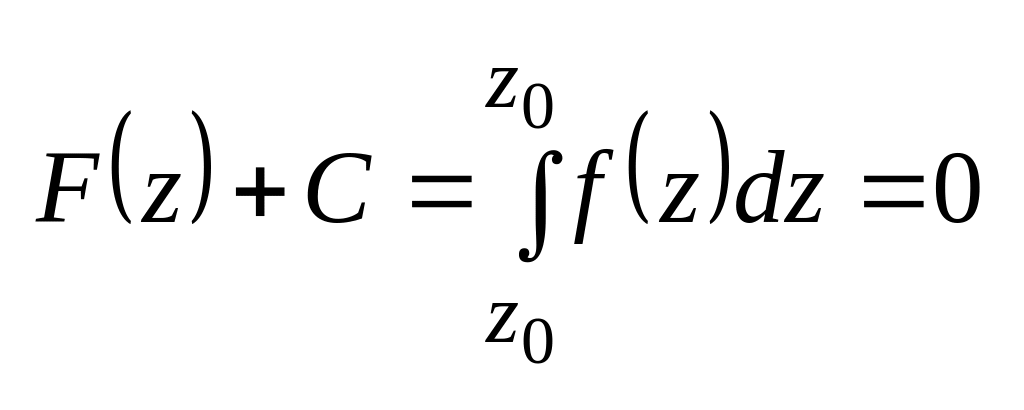 ,то

; .

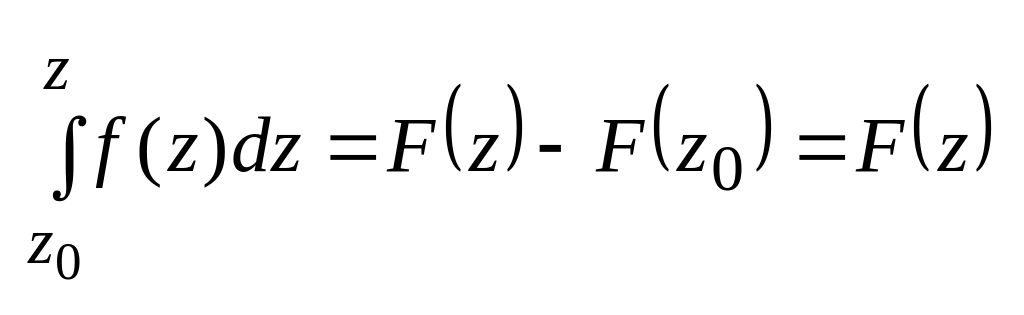
Интегральная формула Коши.

Инт. Формула Коши связывает значение аналитической ункции внутри области с граничными точками .

Пусть область -односвязная с границей , -аналитическая функция. Если -внутренняя точка бласти

(инт. Формула Коши для односвязной области) (5)

Док-во: Пусть есть внутренняя точка области , тогда функция аналогична в области всюду, кроме точки .

Проведем круг с радиусом с центром в

По теореме Коши для многосвязной области

-функция непрерывная, потому, взяв

-произвольно малое число, то

.

2.4. Ряды Тейлора и Лорана. Разложение функций в ряд Лорана. Изолированные особые точки.

Всякая аналитическая в кольце функция может быть разложена в ряд Лорана:

Первая часть называется правильной а вторая главной. Правильная часть сводится к функции f(z) аналитичной в круге |z-z₀|<R, а главная часть сводится к функции аналитичной в кольце |z-z₀|>r . Таким образом ряд Лорана сводится f(z)=f₁(z)+f₂(z) в кольце r<|z-z₀|<R. При разложении функции в ряд Лорана аналитичной не в кольце, а в круге сводится к разложению ряда Тейлора.

Точка Z называется устранимой особой точкой, если главная часть ряда Лорана равна нулю.

Точка Z называется полюсом, если главная часть ряда Лорана имеет конечное число слагаемых.

Точка Z называется существенной особой точкой, если главная часть ряда Лорана состоит из бесконечного числа слагаемых.