1.8. Точки в четвертях и октантах пространства.

Точка может находиться в любом из восьми октантов (нумерацию октантов см. на рисунке 1.23). Следовательно, нужно знать не только расстояние данной точки от той или иной плоскости координат, но и направление, по которому надо это рас­стояние отложить; для этого координаты точек выражают относительными числа­ми. Для отсчета координат применяется система знаков, указанная на рис.1.23, которая называется «правой». Правая система характеризуется тем, что поворот на 90° «положительного» луча Ох (рис.1.23) в сторону «положительного» луча Oy происходит против часовой стрелки (при условии, что мы смотрим на плоскость xOy сверху).

Необходимость использования четвертей и октантов пространства возникает при решении некоторых задач, например при нахождении проекций точки пересечения прямых или прямой и плоскости, которые пересекаются за пределами первого октанта. Плоскости V и H при пересечении образуют четыре двугранных угла, кото­рые называют квадрантами или четвертями пространства. На ри­сунке 1.22, а указан принятый порядок отсчета четвертей I, II, III, IV. Ось проекций делит плоскости V и H на полуплос­кости, условно обозначаемые H и –Н, V –V. На рисун­ке 1.22, б приведен чертеж точек А, В, С, D, E, расположенных в различных четвертях пространства (рис. 1.22, а).

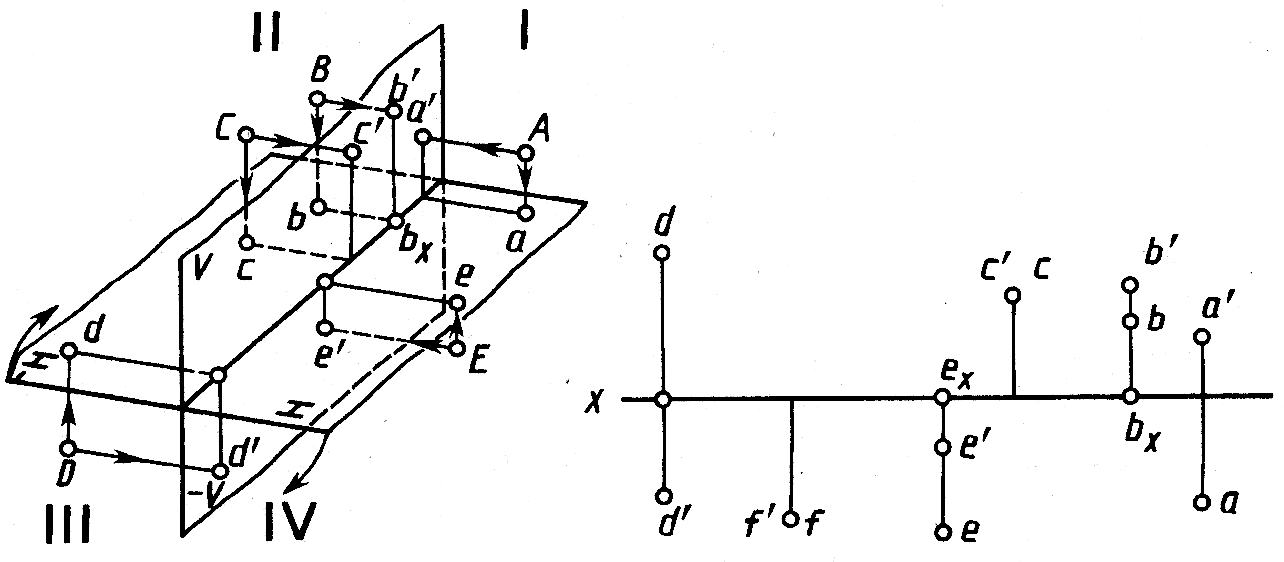
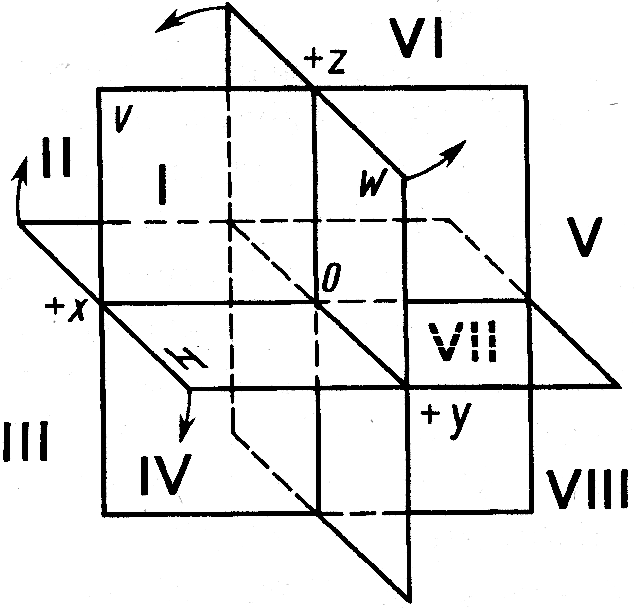
а б

Рис.1.22 Рис.1.23

Точка А расположена в первой четверти. Ее проекции на чертеже (рис.1.22,б) аналогичны чертежу на рисунке 1.14. Точка В ближе к V, чем к –Н; на чертеже bb_x<b'b_x. Точка С одинаково удалена от –Н и от V; проекции с' и с совпадают между собой. Точка D расположена в третьей четверти. Гори­зонтальная проекция d получается над осью проекций, фрон­тальная d' – под осью проекций. Точка D расположена от –V дальше, чем от –Н, поэтому на чертеже dd_x>d'd_x. Точка E расположена в четвертой четверти. Точка E ближе к H, чем к –V; е'е_х<ее_х. Точка F (на рис. 1.22, а не показана) одинако­во удалена от –V и от H, поэтому ее фронтальная f' и горизон­тальная f проекции совпадают.

Система из трех плоскостей проекций показана на рисун­ке 1.23. В своем пересечении они образуют восемь трехгранных углов – восемь октантов. Их нумерация – I, II, III, IV, V, VI, VII, VIII – приведена на этом рисунке. Из рисунков 1.22, а и 1.23 видно, что четверти пространства нумеруются как I – IV октанты.

Система знаков для отсчета координат x, у, z точек в октантах (в соответствии с рис. 1.22) будет следующая:

октант I (+, +, +); октант V (– , +, +);

октант II (+, – , +); октант VI (– ,– , +);

октант III (+, – , – );. октант VII (– , – , – );

октант IV (+, +, – ); октант VIII (– , +, – ).

Например, точка (–25; +15; –10) находится в октанте VIII, а точка (–25; –10; –10) – в октанте VII.

Проекции точки, располо­женной в I октанте, не могут наложиться одна на другую. Это же относится к точкам, рас­положенным в VII октанте. Для остальных октантов две или все три (для II и VIII октантов) проекции одной и той же точки могут оказаться наложенными друга на друга.

Контрольные вопросы к главе 1.

1. Как строят центральную проекцию точки?

2. В каком случае центральная проекция прямой линии является точкой?

3. В чем заключается способ проецирования, называемый параллельным?

4. Как строят параллельную проекцию прямой линии?

5. Может ли параллельная проекция прямой линии представлять собой точку?

6. B каком случае при параллельном проецировании отрезок прямой линии проецируется в натуральную величину?

7. Как расшифровывается понятие «ортогональный»?

8. Как читается свойство проецирования прямого угла?

9. Что такое эпюр Монжа?

10. Что такое система V, H и как называют плоскости проекции V и H?

11. Что называют осью проекций?

12. Как строят проекции точки в системе V, H;

13. Что такое система V, H, W и как называют плоскость проекции W?

14. Как строят профильную проекцию точки по ее фронтальной и горизонтальной проекциям?

15. Что такое прямоугольные координаты точки и в какой последова­тельности их записывают в обозначении точки?

16. Что такое октанты?

17. В каком октанте значения координат по всем осям отрицательные?