Развертка боковой поверхности прямого кругового конуса представляет собой круговой

сектор с углом 180° при вер­шине, где d – диаметр основания, l – длина образующей

Кону­са. Построение сектора (рис. 9.9) выполняют с разбивкой его на равные части соответственно разметке образующих на чер­теже (см. Рис. 9.8 конуса).

Рис.9.9

Используя положение образующих на чертеже и на разверт­ке, находят положение точек на развертке при помощи нату­ральных величин отрезков от вершины до соответствующих точек линии пересечения на чертеже. При этом расстояния S₀A₀ и S₀B₀ соответствуют фронтальным проекциям s'a', s'b'. Отрез­ки образующих от вершины до других точек проецируются на фронтальную плоскость проекций с искажениями. Поэтому их натуральную величину находят вращением вокруг оси конуса до положения, параллельного фронтальной плоскости проек­ций. Например, положение точки D₀ на развертке найдено при помощи отрезка s'd'₁ – натуральной величины образую­щей от вершины S до точки D, точки Е₀ – при помощи отрез­ка s'e'₁ (или s"e'').

Полная развертка поверхности усеченного конуса состоит из трех частей: 1) развертки боковой поверхности, ограничен­ной дугой окружности радиуса l, кривой B₀Q₀F₀E₀D₀C₀A₀ и симметрично ей; 2) .круга основания; 3) натурального вида фигу­ры сечения.

На рисунке 9.8 показано построение фронтальной и гори­зонтальной проекций точки К по изображению К₀ этой точки на развертке (см. рис. 9.9). Для построения проведена образу­ющая S₀13₀ через точку К₀ на развертке. С помощью отрезка l₁, построена горизонтальная проекция 13. Через нее проведены горизонтальная s–13 и фронтальная s'–13' проекции образу­ющей S–13. Отрезок S₀K₀ = s'k'₁ отмечен на проекции образу­ющей s'7'. Обратным вращением построена фронтальная проекция k' точки К на фронтальной проекции образующей s'13'. Горизонтальная проекция k построена с помощью линии связи.

9.4. Пересечение сферы и тора плоскостью. Пример построения линии среза на

поверхности тела вращения сложной формы.

Пересечение сферы плоскостью. Плоскость всегда пересекает сферу по окружности, которая проецируется в виде отрезка пря­мой, в виде эллипса или в виде окружности в зависимости от поло­жения секущей плоскости по отношению к плоскости проекции. Так, на рисунке 9.10 изображены проекции линий пересечения сферы и плоскостей горизонтальной P (P_v) и фронтальной S (S_h). Они пересекают сферу по окружности с центрами С (c' с, с") и С\ (с'₁ с₁ с"₁) с проекциями в виде окружности и отрезка прямой.

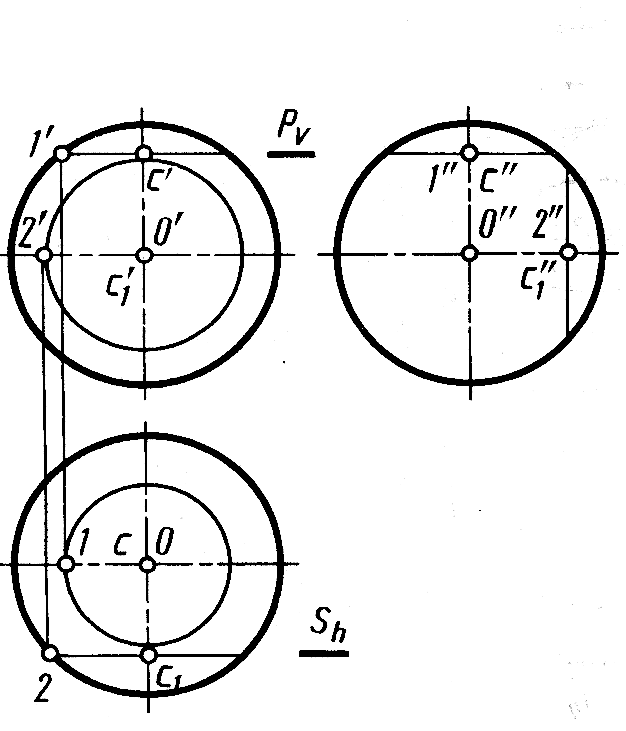
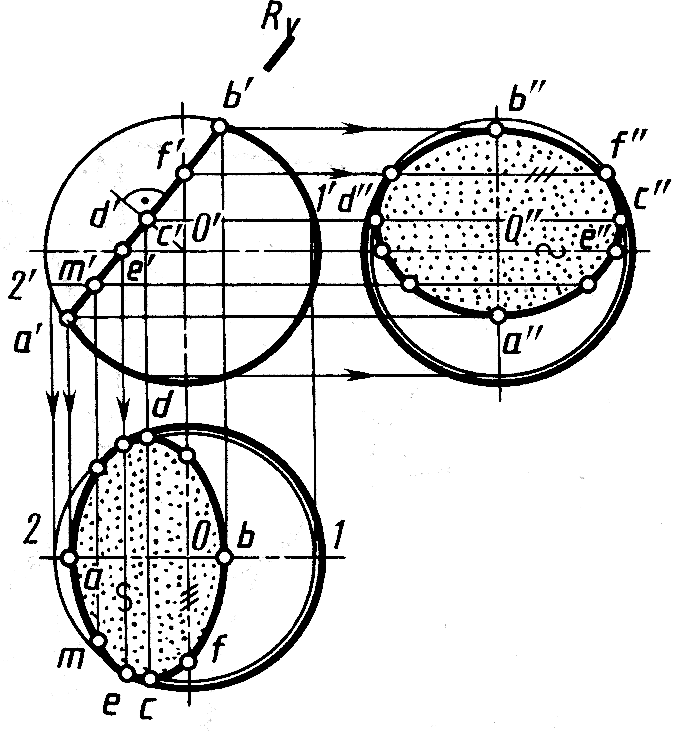
Рис.9.10 Рис. 9.11

В примере, приведенном на рисунке 9.11, горизонтальная и про­фильная проекции линии пересечения сферы фронтально-про­ецирующей плоскостью – эллипсы, длины больших осей которых cd и c"d" paвны величине диаметра окружности (a'b'). Малые оси эллипсов ab и a"'b" получают проецированием. На рисунке 9.11 показано построение проекций некоторых точек. Проекции с и d построены на горизонтальной проекции параллели радиуса 0 – 1, построенной с помощью проекции 1' . Проекции с" и d" построены на профильной проекции окружности, проведенной на сфере через проекции с' (d') так, что плоскость окружности параллельна плоскости проекций. Проекция e является точкой касания эллипса (горизонтальной проекции окружности среза) и экватора сферы. Она построена в проекционной связи на гори­зонтальной проекции экватора по фронтальной проекции e'. Го­ризонтальная проекция m произвольной точки на линии среза построена с помощью параллели радиуса 0 – 2, фронтальная про­екция которой проходит через проекции m' и 2'. Проекция f" является точкой касания эллипса (профильной проекции окруж­ности среза) и профильной проекции очерка сферы.

Если плоскость, пересекающая сферу, является плоскостью общего положения, то задачу решают способом перемены плоскос­тей проекций. Дополнительную плоскость проекций выбирают так, чтобы обеспечить перпендикулярность ее и секущей плоско­сти. Это позволяет упростить построение линии пересечения.

Линию пересечения тора плоскостью в общем случае строят при помощи вспомогательных плоскостей, пересекающих тор и секущую плоскость. При этом подбирают плоскости, пересе­кающие тор по окружности, т. е. расположенные перпенди­кулярно оси тора или проходящие через его ось.

В примере на рисунке 9.12 показано применение вспомога­тельных плоскостей T₁ (T_1v) и T₂ (T_2v), перпендикулярных к оси тора, для построения линии пересечения и натурального вида фигуры сечения поверхности тора плоскостью P (Р_w).

Тор на рисунке 9.12 имеет два изображения – фронтальную проекцию и половину профильной проекции. Полуокружность радиуса R₁ (про­фильная проекция линии пересечения тора вспомогательной плос­костью T₁) касается проекции плоскости P (следа P_w). Тем самым

определяются профильная проекция 3" (o"3" P_w) и по ней фронтальная проекция 3' одной из точек проекции искомой линии пе­ресечения.

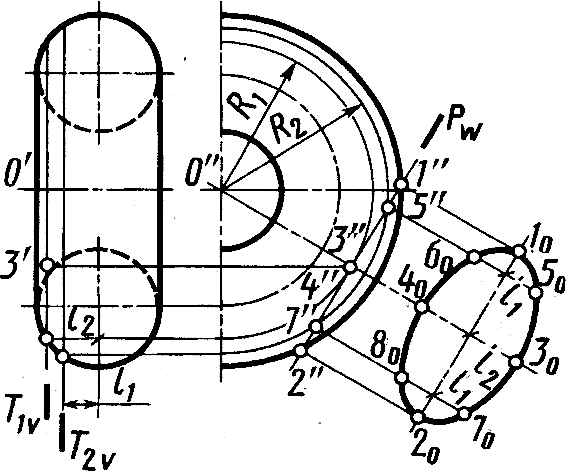
Рис.9.12

Полуокружность радиу­са R₂ – профильная проекция линии пересечения тора вспомогательной плоскостью Т₂. Она пересекает про­фильную проекцию плоскости P (след Р_w) в двух точках 5" и 7" – профильных проекциях точек линии пересечения. Проводя аналогичные построения, можно получить необ­ходимое количество проекций точек для искомой линии пересе­чения. Используем найденные точки для построения натуральной величины сечения. Фигура сечения тора плоскостью, парал­лельной его оси, имеет оси и центр симметрии. При ее постро­ении использованы расстояния l₁, и l₂ на фронтальной проекции для нанесения точек 5₀, 7₀ и 3₀ . Точки 6₀, 8₀ и 4₀ построены как симметричные. Построенная кривая пересечения поверхности тора плоскостью выражается алгебраическим уравнением 4-го порядка.

Кривые пересечения тора с плоскостью, параллельной оси, приведены на рисунке 9.13. Они имеют общее название – кривые Персея (Персей – геометр Древней Греции). Это кри­вые 4-го порядка. Вид кривых зависит от расстояния секущей плоскости до оси тора.

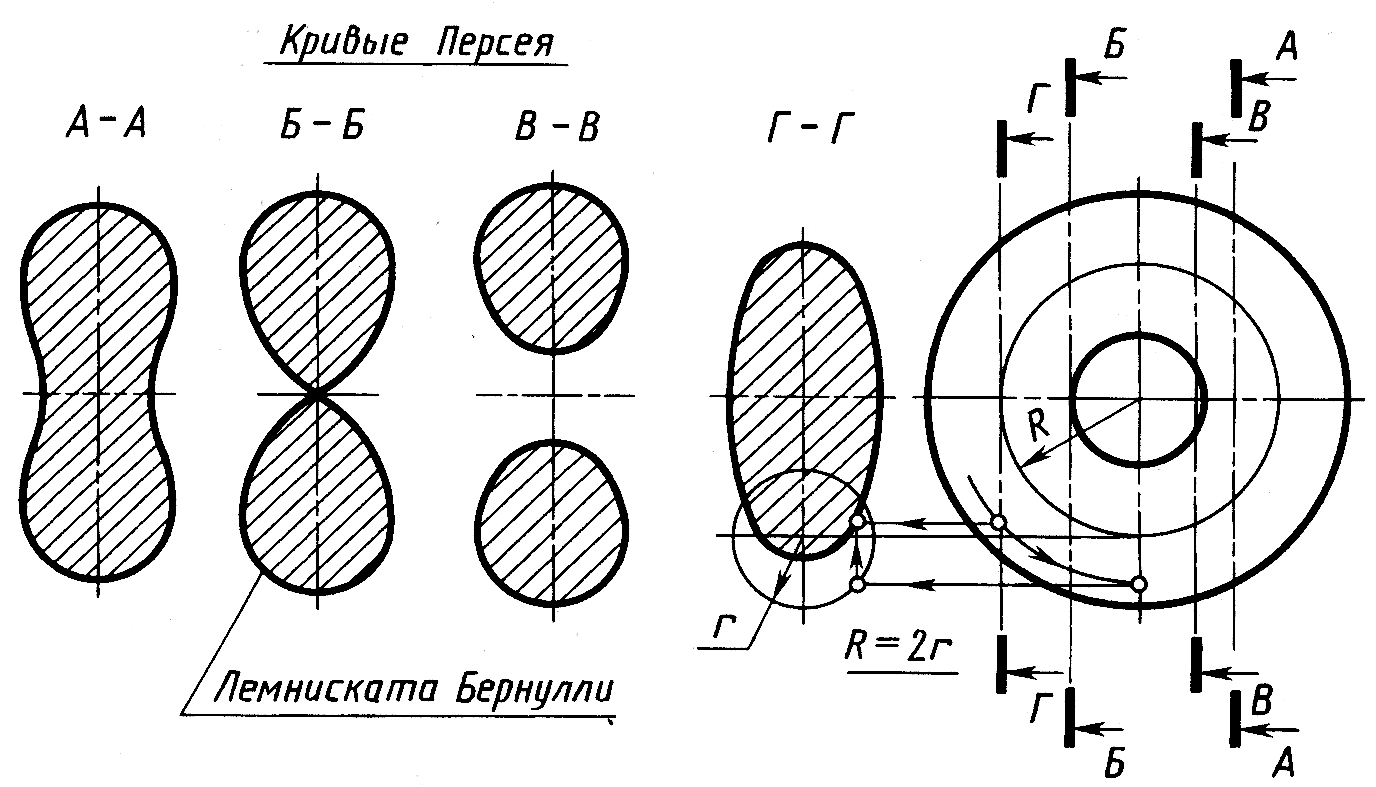
Рис.9.13

Многие детали приборов и машин имеют в своей основе форму тела вращения со сложной формой поверхности. Такое тело можно рассматривать как состоящее из частей элементар­ных тел вращения – цилиндра, конуса, сферы и тора или круго­вого кольца. Детали из такого тела вращения часто конструируют путем среза части тела плоскостью, параллельной оси. При этом в пересечении поверхности тела с плоскостью среза образуют­ся сложные линии, построение которых и рассмотрено ниже. Эти линии, являющиеся частным случаем линии пересечения поверхности вращения с плоскостью (плоскость параллельна оси), называются линиями среза.