
- •Начертательная геометрия
- •Инженерная графика
- •Содержание введение ………………………………………………………………………………………………... 4
- •2.2. Положение прямой линии относительно плоскостей проекций.
- •2.3. Определение натуральной величины отрезка прямой общего
- •Развертки ………………………………………………………………………………………….. .. 70
- •Введение
- •1. Метод проекций
- •1.1. Центральные проекции.
- •1.2. Параллельные проекции.
- •1.3. Свойства центральных и параллельных проекций.
- •1.4. Метод Монжа.
- •1.5. Проецирование на две взаимно перпендикулярные плоскости проекций
- •1.6. Проецирование на три взаимно перпендикулярные плоскости проекций
- •1.7. Ортогональные проекции и система прямоугольных координат.
- •1.8. Точки в четвертях и октантах пространства.
- •2. Проецирование отрезка прямой линии
- •2.1. Проецирование отрезка прямой.
- •2.2. Положение прямой линии относительно плоскостей проекций. Особые
- •2.3. Определение натуральной величины отрезка прямой общего положения и
- •2.4. Взаимное положение прямых
- •3. Плоскость
- •3.1. Способы задания плоскости на чертеже
- •3.2. Положение плоскости относительно плоскостей проекций
- •3.3. Прямая и точка в плоскости
- •3.4. Прямые особого положения в плоскости – главные линии плоскости
- •Взаимное положение прямой линии и плоскости,
- •4.1. Пересечение прямой линии с проецирующей плоскостью
- •4.2. Пересечение двух плоскостей
- •4.3. Пересечение прямой линии общего положения с плоскостью общего
- •4.4. Построение линии пересечения двух плоскостей по точкам пересечения
- •Построение взаимно параллельных прямой линии и плоскости и двух
- •Построение взаимно перпендикулярных прямой и плоскости,
- •Угол между прямой и плоскостью
- •Способы преобразования чертежа
- •5.1. Общая характеристика способов преобразования чертежа
- •5.2. Способ перемены плоскостей проекций
- •5.3. Способ вращения
- •6. Кривые линии
- •6.1. Общие сведения о кривых линиях и их проецировании
- •6.2. Построение проекций окружности
- •6.3. Построение проекций цилиндрической винтовой линии
- •7. Поверхности
- •7.1. Общие сведения о поверхностях и их изображении на чертежах
- •Чертеж гиперболического параболоида, называемого косой плоскостью, приведен на рисунке 7.6.
- •7.2. Винтовые поверхности
- •7.3. Поверхности и тела вращения
- •8. Изображение многогранников
- •8.1. Применение многогранников в технике
- •8.2. Чертежи призмы и пирамиды
- •8.3. Пример определения высоты пирамиды и угла между ее гранями
- •8.4. Пересечение многогранников плоскостью
- •8.5. Построение точек пересечения прямой с поверхностью многогранника
- •8.6. Взаимное пересечение многогранников
- •8.7. Развертка гранных поверхностей
- •9. Пересечение поверхностей плоскостью и прямой линией, развертки.
- •9.1. Общие приемы построения линии пересечения поверхности плоскостью
- •9.2. Пересечение цилиндрической поверхности плоскостью. Построение развертки
- •9.3. Пересечение конической поверхности плоскостью. Построение развертки
- •Развертка боковой поверхности прямого кругового конуса представляет собой круговой
- •Конуса. Построение сектора (рис. 9.9) выполняют с разбивкой его на равные части соответственно разметке образующих на чертеже (см. Рис. 9.8 конуса).
- •9.4. Пересечение сферы и тора плоскостью. Пример построения линии среза на
- •9.5. Пересечение прямой линии с поверхностью.
- •10. Пересечение поверхностей
- •10.1. Общие сведения о пересечении поверхностей
- •Повторяя такие построения многократно с помощью аналогичных вспомогательных поверхностей, находят необходимое число общих точек двух поверхностей для проведения линии
- •Нии пересечения поверхностей:
- •10.2. Применение вспомогательных секущих плоскостей
- •10.3. Применение вспомогательных сфер с постоянным центром
- •10.4. Применение вспомогательных сфер с переменным центром
- •10.5. Некоторые особые случаи пересечения поверхностей
- •10. Аксонометрические проекции
9.2. Пересечение цилиндрической поверхности плоскостью. Построение развертки
Для построения линии пересечения цилиндрической поверхности плоскостью в общем случае находят точки пересечения образующих с секущей плоскостью. При необходимости не исключается применение и вспомогательных секущих плоскостей, пересекающих поверхность и плоскость.
Заметим, что любую цилиндрическую поверхность плоскость, расположенная парал-лельно образующей этой поверхности, пересекает по прямым линиям (образующим).



Рис.9.1 Рис.9.2 Рис.9.3
Вид линии, образованной при пересечении плоскостью прямого кругового цилиндра, определяется положением плоскости относительно оси. Эта линия – окружность, если плос-кость перпендикулярна оси; две прямые (проекции l'2' и 3'4' на рис. 9.1) или одна прямая (касательная), если плоскость параллельна оси (след Pw); эллипс (1–2–3–4 на рис. 9.2), если плоскость расположена под углом к оси.
Образование выреза на цилиндре двумя плоскостями P (Pv)║W и T(Tw) ║V показано на рисунке 9.3.
Цилиндр с наклонным срезом. Рассмотрим построение чертежа цилиндра со срезом проецирующей плоскостью под некоторым углом к его оси (не равным 0° и 90°), натуральной величины среза и развертки цилиндра (рис. 9.4, 9.5).
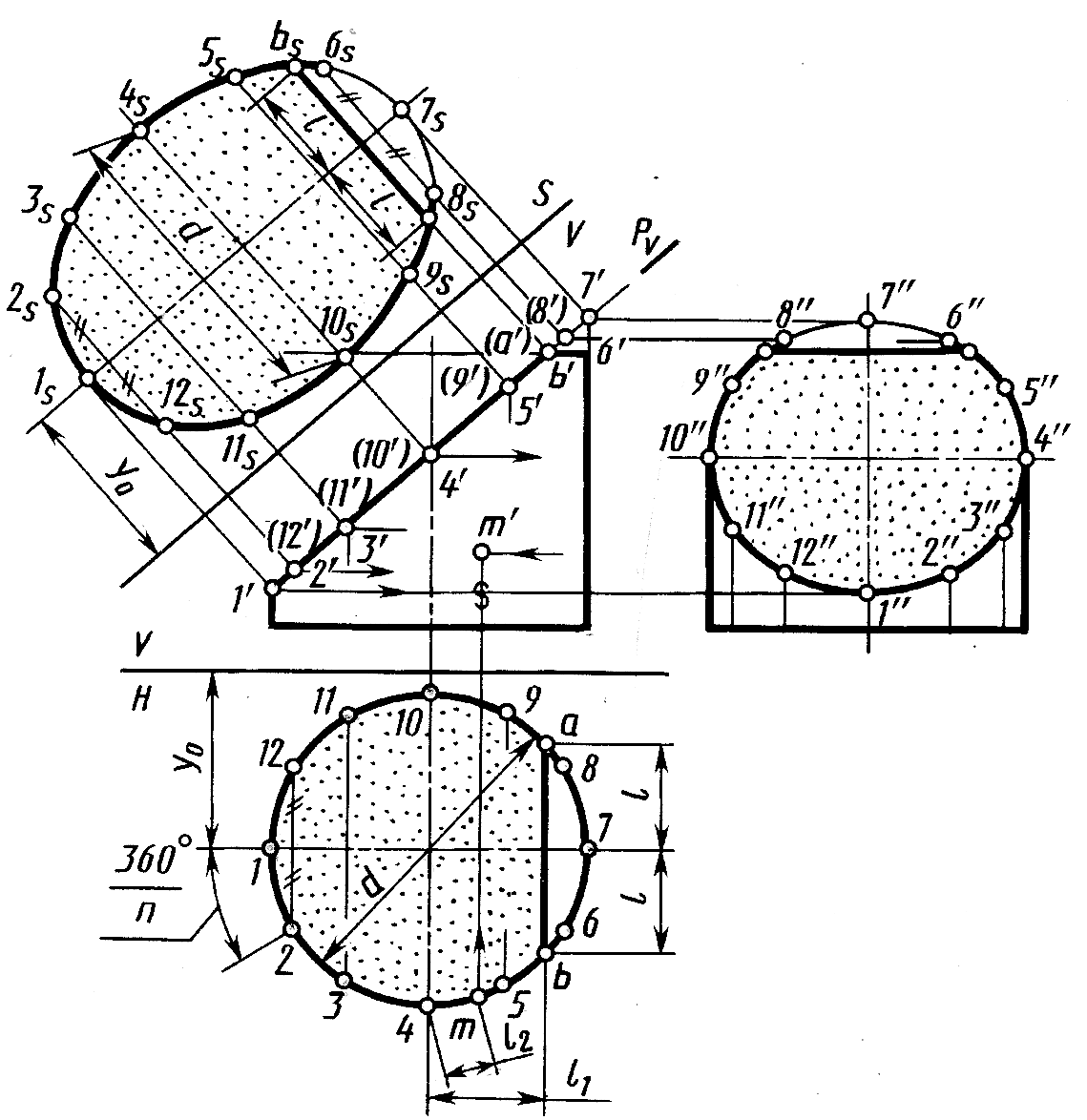
Ри.9.4
Ось цилиндра и вся цилиндрическая поверхность перпендикулярны плоскости H. Следовательно, все точки цилиндрической поверхности, в том числе и линия пересечения ее с плоскостью P(Pv) проецируются на плоскость Н в окружность. На ней отмечают горизонтальные проекции точек 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 12 эллипса, расположив их равномерно по окружности. В проекционной связи строят фронтальные проекции 1', 2', 3', 4', 5', 6', 7', 8', 9', 10', 11', 12' отмеченных точек на фронтальном следе Рv секущей плоскости. Профильные проекции тех же точек строят по их горизонтальной и фронтальной проекциям на линиях связи.
Профильная проекция линии пересечения цилиндра с секущей плоскостью – эллипс, большая ось 10"4" которого в данном случае равна диаметру цилиндра, а малая 1"7" – профильная проекция отрезка 1 – 7.
Если плоскость P расположить (рис. 9.4) под углом 45° к оси, то профильная проекция эллипса фигуры сечения будет окружность.
Если острый угол между осью цилиндра и секущей плоскостью будет меньше 45°, то малая ось эллипса на профильной проекции (рис. 9.4) станет равной диаметру цилиндра.
Натуральный вид фигуры сечения цилиндра плоскостью P построен способом перемены плоскостей проекций на плоскости S, перпендикулярной плоскости V. Большая ось эллипса – отрезок 1S7S =1'7', малая – отрезок 4S10S = d.
Построение развертки (рис.9.5). Полная развертка состоит из четырех частей: развертки боковой поверхности, ограниченной пятью отрезками прямой линии и кривой А010В0 – синусоидой; натурального вида фигуры сечения; круга основания цилиндра; сегмента, полученного на верхнем основании.

Рис.9.5
Полная развертка боковой поверхности цилиндра – прямоугольник с высотой, равной высоте цилиндра, а длиной L = nd, где d – диаметр цилиндра. Для построения на развертке точек линии среза развертку основания цилиндра делят на такое же число частей, как и при построении проекций линий среза. Проводят через точки деления образующие и, пользуясь фронтальной проекцией, отмечают на них высоту до точек эллипса среза – точки 10, 20 и 120, 30 и 110, 40 и 100 , 50 и 90, 60 и 80, 70. Соединяют построенные точки плавной кривой – сину-соидой. Натуральный вид фигуры среза цилиндра плоскостью выполнен ранее (1S2S3S...12S), и его по координатам строят на развертке.
Построим на чертеже цилиндра проекции точки M, указанной на развертке точкой М0. Для этого отметим хорду l2 между образующей, на которой расположена точка М0, и образующей точки 4. По хорде l2 строим горизонтальную проекцию m (рис. 9.4) и по известной высоте ее расположения находим ее фронтальную проекцию m'.
