
- •Министрество связи и массовых коммуникаций российской федерации поволжский государственный университет телекоммуникаций и информатики Кафедра торс
- •Структурная схема системы передачи
- •2. Исследование тракта кодер-декодер источника
- •3.Исследование тракта кодер-декодер канала.
- •Исследование тракта модулятор – демодулятор
- •5. Демонстрация работы системы передачи
- •Список использованных источников:
Исследование тракта модулятор – демодулятор
Определим скорость амплитудной модуляции:
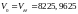 [бит/с]
[бит/с]
Найдем тактовый интервал передачи одного бита
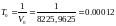 [c]
[c]
Рассчитаем минимально необходимую полосу пропускания канала.
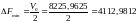 [Гц]
[Гц]
Частота несущего колебания в 100 раз больше скорости модуляции:
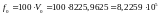 [Гц]
[Гц]
При АМ полоса частот передаваемого сигнала:
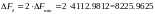 [Гц]
[Гц]
Запишем аналитическое выражение АМ-сигнала в общем виде
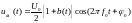
Здесь
b(t)
– первичный
сигнал, представляющий двоичные символы
на выходе кодера канала (нулю соответствует
b(t)
= – 1,
единице b(t)
= 1).
U0,
f0
и
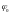 -
соответственно амплитуда, частота,
начальная фаза несущего колебания (
можно положить равной нулю).
-
соответственно амплитуда, частота,
начальная фаза несущего колебания (
можно положить равной нулю).
Выражения для сигналов, соответствующих передаче 0 и 1:
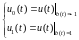
Тогда:

Запишем аналитическое выражение, связывающее сигналы на входе и выходе.
Учитывая, что у нас гауссовский канал с неопределенной фазой, выражения примут вид.
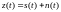 ,
где
,
где
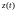 -сигнал
на выходе модулятора
-сигнал
на выходе модулятора
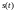 -сигнал
на входе модулятора
-сигнал
на входе модулятора
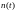 -
шум
-
шум
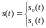
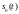 и
и
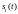 сигнал,
соответствующий приему 1 и 0:
сигнал,
соответствующий приему 1 и 0:
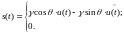
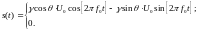
Тогда:
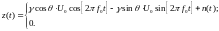
Найдем
амплитуду
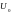 .
.
Выразим амплитуду несущего колебания из выражения для вычисления мощности
единичного сигнала на передаче.
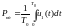
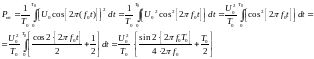

Теперь
найдем
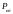 .
.
Так как по условию у нас некогерентный прием, то
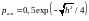 ,
,
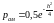 ,
,
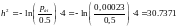
Найдем энергию единичного сигнала из формулы
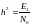 ,
,
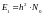 ,
,
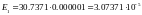 [
[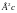 ]
]
Найдем мощность единичного элемента сигнала на приеме
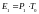 ,
,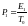 [
]
[
]
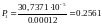 [
[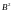 ]
]
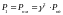 ,
,
Отсюда:
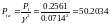 [
[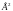 ]
]
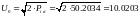 [
[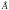 ]
]
3.Некогерентный приём сигналов. Алгоритм работы демодулятора.
Если
значение начальной фазы приходящего
сигнала не известно и может принимать
любое значение на интервале
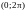 ,
то такой метод приема называется
некогерентным.
,
то такой метод приема называется
некогерентным.
Для
вывода правила оптимального некогерентного
приёма будем исходить из логарифма
отношения правдоподобия
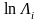 для
сигнала
для
сигнала
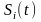 ,
,
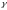 -
известный коэффициент передачи канала,
а
-
известный коэффициент передачи канала,
а
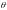 -
случайный сдвиг в канале, тогда:
-
случайный сдвиг в канале, тогда:
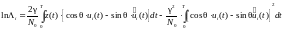
Здесь
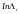 является случайной величиной, принимающий
различные значения при различных
является случайной величиной, принимающий
различные значения при различных
 .Правило
максимума правдоподобия в такой ситуации:
.Правило
максимума правдоподобия в такой ситуации:
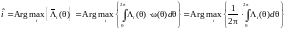
При
нахождении
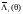 заметим, что второй интеграл в правой
части ( предыдущей формулы) от
заметим, что второй интеграл в правой
части ( предыдущей формулы) от
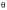 не зависит и равен энергии
не зависит и равен энергии
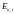 сигнала
сигнала
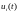 на входе канала.
на входе канала.
Учитывая,
что
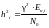 ,
получаем:
,
получаем:
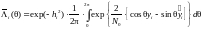 ,
,
Где
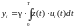 ;
;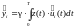
Обозначив
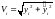 и
и
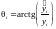 ,
можно записать:
,
можно записать:
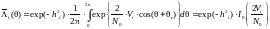 ,
где
,
где
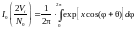 -
модифицированная функция Бесселя
нулевого порядка.
-
модифицированная функция Бесселя
нулевого порядка.
Вместо того, чтобы сравнивать отношения правдоподобия , можно сравнить их логарифмы, что приводит к следующему алгоритму:
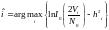
Для двоичной системы сигналов правило оптимального некогерентного приема выражается неравенством:
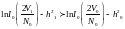
При выполнении этого неравенства регистрируется 1, в противном случае 0.

Рис. 3. Квадратурная cхема реализации оптимального приёма дискретных сообщений при неопределённой фазе сигнала.
4. Найдем минимально необходимую мощность сигнала на приемной и передающей стороне
[ ]
[ ]
Найдем среднюю мощность сигнала на приеме.
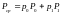 ,
,
Для
АМ
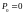 ,
следовательно:
,
следовательно:
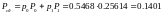 [
]
[
]
5. Определим пропускную способность непрерывного канала связи.
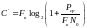 [бит/с]
[бит/с]
Для
начала найдем полосу частот передаваемого
сигнала
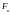 .
.
При АМ:
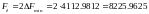
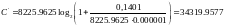 [бит/с]
[бит/с]
Рассчитав пропускную способность, мы заметили, что она больше скорости модуляции,
что говорит о правильно проделанных расчетах.
6. Определим вероятность ошибки на выходе демодулятора при использовании других
видов модуляции при сохранении пиковой мощности сигнала.
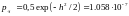
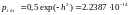
. Из проделанных выше расчетов мы видим, что у АМ самая большая вероятность ошибки. При ОФМ самая маленькая вероятность ошибки, это говорит о том, что самый эффективный вид модуляции – ОФМ .
