
- •Тема 2.
- •2.1. Из теории графов.
- •1.2. Понятие графа и его составляющие.
- •2.3 Связные графы.
- •2.4. Поиск путей в графе.
- •2.5. Задача Эйлера.
- •2 .6. Плоские графы и формула Эйлера.
- •2.7. Задачи о раскрасках графа.
- •Тема 3.
- •3.1. Представление графов матрицами.
- •3.2. Код Харари.
- •3.3. Деревья и ордеревья.
- •3.4. Бинарные деревья и их представление в памяти.
- •3.5. Код Прюфера.
- •3.6. Обход деревьев.
- •3.7. Деревья и списки.
- •3.8. Поиск в дереве.
3.5. Код Прюфера.
Немецкий математик К.Прюфер изобрёл способ представления любых деревьев и ордеревьев. Изложим алгоритм построения кода Прюфера.
Пусть имеется дерево с n пронумерованными вершинами. В списке всех вершин слева направо ищем первую висячую вершину. Пусть это a1. Ищем единственную вершину b1 с которой смежна a1. Величину b1 заносим в новый список – будущий код Прюфера, а вершину a1 вычеркиваем и из списка, и из дерева. Этот процесс повторяем n-2 раза. В результате получим новый список. {b1, b2,…, bn-2} – это и есть код Прюфера. Заметим, что в процессе построения дерево все время уменьшается, и возникают новые висячие вершины
Пример.
Построить код Прюфера для дерева.
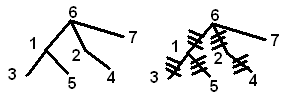
Список всех вершн
1
2
3
4
5
6 7.
N=7; отсюда n-2=5.
В этом списке слева направо ищем первую висячую.
{1; 1; 6; 2; 6;} – код Прюфера.
Доказано, что код Прюфера определяет дерево однозначно. Более того, любой список { b1, b2,..,bn-2} чисел от 1 до n является кодом Прюфера некоторого дерева.
Пример 2.
Восстановить дерево по коду Прюфера.
{1; 3; 6; 5; 3; 2; 7;}
n-2=7; n=9.
1
2
3
4
5
6
7 8
9
Введем понятие неприкосновенной вершины: если вершина встречается в коде Прюфера дальше, то она неприкосновенна
Д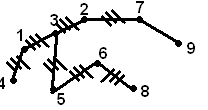 обавляем
оставшиеся вершины.
обавляем
оставшиеся вершины.
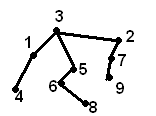
Перестроим дерево.
Теорема Кэш.
Общее число деревьев с n пронумерованными вершинами равно nn-2/
Доказательство.
Таких деревьев ровно столько, сколько кодов Прюфера. b – число от 1 до n.
По правилу произведения nn-2
Например, для n=5, получим 55-2=152 раз.
3.6. Обход деревьев.
Часто необходимо обойти все вершины дерева или ордерева не хаотично, а по определённому алгоритму.
Самые простые алгоритмы обхода для бинарного ордерева. Из 3 на выбор.
1)Прямой метод – обойти корень, затем левое поддерево, затем правое (КЛП)
Этот принцип соблюдается в любой момент времени.
2)Обратный метод: обойти левое поддерево, корень, правое поддерево (ЛКП)
3)Концевой метод: обойти левое поддерево, правое, корень (ЛПК)
Обойти 3 способам данное бинарное дерево (не менее 10 вершин)
1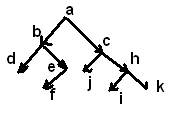 )
Прямой
(КЛП)
a b d e f c g h I k
)
Прямой
(КЛП)
a b d e f c g h I k
2) Обратный (ЛКП) d b f e a g c I h k
3) Концевой (ЛПК) d f e b g I k h c a
Для не бинарных деревьев и ордеревьев алгоритм гораздо сложнее.
3.7. Деревья и списки.
Бытовое понятие списков всем известно, но в информатике имеется формальное понятие списка.
Опр. Назовем атомом любой неделимый объект (букву, цифру и т.д.). Списками называется последовательность атомов и списков, разделенных запятыми и заключенными в общие скобки.
Это так называемая рекурсивное определение (использующие само себя). В математике это запрещается, а информатике широко применяется.
Примеры списков.
Атомы – буквы.
(а)
(a,b)
(a,b,c)
(a, (b,c))
((a,b),c)
(a,((b,c),d),((e,f),g))
Каждому списку можно сопоставить ордерево, действуя по правилу
Атомом или списком, заключенным в общие скобки, соответствует общая безымянная вершина, потомками которой они являются.
П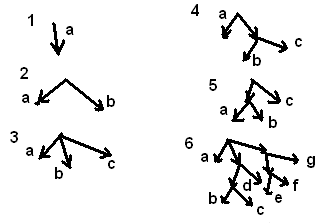 ример.
ример.
Видим, что атомам соответствуют только висячие вершины дерева. Поэтому обратная связь такова: каждому дереву соответствует список его висячих вершин.
Вводится понятие глубины списка: наибольшее число вложенных друг в друга скобок.
При этом глубина списка совпадает с глубиной соответствующего дерева (число уровней).
