Тема 3.

Графы как структурные обработки данных.

Здесь изучают различные способы представления графов в памяти компьютера. Они применяются во многих алгоритмах в задачах поиска информации. Существует несколько подходов к представлению данных в графе в памяти компьютера: матрицы, списки, коды.

3.1. Представление графов матрицами.

Напомним, что матрица – прямоугольная таблица чисел.

А=

A_ij – элемент i-строки, j-столбца.

Матрица размером m x n.

Если m=n – матрица называется квадратной.

В программе матрицы называют двумерными массивами.

Матрица смежности.

Опр. Пусть дан орграф с n пронумерованными вершинами. Матрица А размера m x n, заполненная числам , назывется матрицой смежности орграфа.

Она определяет орграф однозначно (по матрице можно восстановить граф)

Недостаток матрицы смежности – большое количество нулей (она разрешена).

Если у графа 10 вершин 20 дуг, то из 100 элементов матрицы 80 нулей.

Для неориентированного графа матрица смежности строится точно так же, но он обладает дополнительными хорошим свойствам.

a_ij=a_ji. Это свойство означает симметричность матрицы относительно главной диагонали.

В этом случае нет смысла хранить в память всю матрицу, достаточно ее верхний треугольник А^I

Матрица смежности и число путей.

Заметим, что сама матрица смежности число путей длины 1 из i-й вершины в j-ю

j

i

Нельзя узнать число путей большей длины.

Вспомним операцию умножения матриц (умножение строк на столбцы). Если умножить квадратную матрицу саму на себя, получим квадрат матрицы А²=А*А: А³=А²*А и т. д.

Теорема Степень матрицы смежности А^m заполнена элементам a_ij^m, показывает число путей длины m из i-й вершины в j-ю.

Доказательство

В частности случая m=2

А²⁼А*А заполнена произведениям строк на столбец a_ij=a_i1*a_1j+a_i2*a_2j+a_in*a_nj= 0*0+0*1+1*1

Из этой суммы останется только члены 1*1, то есть a_ik=1 и a_kj=1.

П олучим путь длины 2 из i-й вершины в j-ю, а вся сумма показывает нам число таких путей.

Аналогично доказывается для n=3,4 и т.д.

Матрица инцидентности.

Опр. Пусть в орграфе m вершин и n дуг (все пронумерованы).

Матрица B размером m x n заполняется числам

b_ij=

Можно заметить, что в каждом столбце матрицы инцидентности встречается 1 и -1, остальные – нули (ил же 2 и остальные нули).

Поэтому и эти матрица тоже очень разряжена (при больших m)

Поэтому возникла мысль кроме матриц использовать отдельные числа (коды) для компактного представления графов.

3.2. Код Харари.

Идея Фрэнка Харари (США) – установить матрицу смежности в 1 число.

Пусть дан неориентированный граф. Мы уже знаем, что его матрица смежности А симметрична относительно главной диагонали м достаточно хранить её верхний треугольник А^I. Распишем его в виде двоичной строки (слева направо, сверху вниз).

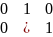-> 0 1^I 0^I 0 1^I 1

Меняем нумерацию вершин графа, точно так же получим другие двоичные строки (числа). Сравним между собой именно как число (по первому биту). Наибольшее из полученных чисел и есть код Харари, а нумерация вершин, давшая это число, называется канонической.

Код Харари определяет граф однозначно. При общении между людьми код Харари принято переводить в десятичное число.

П ример: Найти код Харари графа

А= A^I= -> 0 1 1I 1 0I0

А= A^I= -> 1 1 0^I 0 1^I 0

Вершину с петлей ставим первой, а соседнюю с ней – второй.

Очевидно, увеличить полученное число нельзя, значит, мы получили каноническую нумерацию вершин и код Харари. Переведём в десятичную систему. Получится 50.

Видимо, существует алгоритм, сразу нумерующий вершины графа каноническим образом (учитывая петли и число соседней (степен вершин)).

Заметим, что не всякое десятичное число служит кодом Харари какого-либо графа. Дело в том, что проделав все эти действия в обратном порядке, мы получим граф с нумерацией вершин, который вовсе не обязан быть канонической.