
- •1. . Классификация систем автоматического управления
- •2. Математические модели сау
- •3.Передаточные функции и структурные схемы систем автоматического управления.
- •4. Методы преобразования структурных схем
- •5. 5.Правила преобразования структурных схем.
- •2. Интегрирующие
- •10. Безынерционное звено
- •15. Оценка устойчивости сау по корням характеристического уравнения
- •16. Критерий Гурвица
- •17. Критерий Михайлова
- •19. Логарифмический критерий Найквиста
17. Критерий Михайлова
Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик. Эти критерии позволяют исследовать устойчивость систем высокого порядка и имеют простую геометрическую интерпретацию.
Рассмотрим левую часть характеристического уравнения, которая представляет собой характеристический полином:
D(p) = a0 р n + a1 рn-1 + ... + an-1 р + an
Подставим в этот полином p = jw, где w представляет собой угловую частоту колебаний. При этом характеристический полином принимает вид:
D(jw) = X(w) + jY(w) = D (w)ej(w), где вещественная часть будет содержать четные степени w
X(w) = an - an-2w2 + … (5а)
а мнимая – нечетные степени w:
Y(w) = an-1w - an-3w3 + … (5б)
Функции D (w) и (w) представляют собой модуль и фазу характеристического уравнения.
Характеристический полином не будет иметь корней в правой полуплоскости , если полное приращение фазы (w) при изменении w от 0 до равно n /2, где n – степень полинома D(p).
Для устойчивости системы n-гo порядка необходимо и достаточно, чтобы вектор D (jw), описывающий кривую Михайлова, при изменении w от нуля до бесконечности имел угол поворота = n /2.
18. Критерий устойчивости Найквиста — Михайлова — один из способов судить об устойчивости замкнутой системы управления по её разомкнутой амплитудно-фазовой частотной характеристике. Является одним из частотных критериев устойчивости. С помощью этого критерия оценить устойчивость весьма просто, без необходимости вычисления полюсовпередаточной функции замкнутой системы.
Этот
критерий позволяет судить об устойчивости
замкнутой системы по амплитудно-фазовой
частотной характеристике
(а.ф.х.) ![]() разомкнутой
системы. Условие устойчивости замкнутой
системы сводится к требованию, чтобы
а.ф.х. разомкнутой системы не охватывала
точку
разомкнутой
системы. Условие устойчивости замкнутой
системы сводится к требованию, чтобы
а.ф.х. разомкнутой системы не охватывала
точку ![]() .
На рис. 5.4, а характеристики 1 и 4
соответствуют устойчивым системам,
характеристика 3 – неустойчивой, а
характеристика 2 – нахождению системы
на границе устойчивости. Если, например,
уменьшить коэффициент передачи в
неустойчивой системе, то ее а.ф.х. сожмется
к началу координат, в результате чего
система станет устойчивой. Наоборот,
при увеличении коэффициента передачи
характеристика устойчивой системы в
конце концов охватит точку
и
система потеряет устойчивость.
.
На рис. 5.4, а характеристики 1 и 4
соответствуют устойчивым системам,
характеристика 3 – неустойчивой, а
характеристика 2 – нахождению системы
на границе устойчивости. Если, например,
уменьшить коэффициент передачи в
неустойчивой системе, то ее а.ф.х. сожмется
к началу координат, в результате чего
система станет устойчивой. Наоборот,
при увеличении коэффициента передачи
характеристика устойчивой системы в
конце концов охватит точку
и
система потеряет устойчивость.
|
Данная выше формулировка критерия Найквиста относится к системам, которые являются устойчивыми в разомкнутом состоянии. В случае одноконтурной системы устойчивость в разомкнутом состоянии всегда обеспечивается, если система состоит только из устойчивых звеньев. При наличии местных обратных связей должна быть еще проверена устойчивость образованных этими связями контуров. Для этого, в свою очередь, может быть применен критерий Найквиста или любой другой.
Для
систем, неустойчивых в разомкнутом
состоянии, критерий Найквиста имеет
такую формулировку: для
устойчивости системы в замкнутом
состоянии а.ф.х. разомкнутой системы
должна охватывать точку
.
При этом число пересечений ею отрицательной
действительной полуоси левее точки
сверху
вниз должно быть на ![]() больше
числа пересечений в обратном направлении,
где
больше
числа пересечений в обратном направлении,
где ![]() –
число полюсов передаточной
функции
–
число полюсов передаточной
функции ![]() разомкнутой
системы с положительной действительной
частью.
разомкнутой
системы с положительной действительной
частью.
В
соответствии с критерием Найквиста об
устойчивости можно судить не только по
а.ф.х., но и совместно по амплитудно-частотной
и фазово-частотной характеристикам
разомкнутой системы. Обычно при этом
пользуются логарифмическими
характеристиками, что представляет
большое удобство в силу простоты их
построения. Согласно критерию Найквиста,
для системы, устойчивой в разомкнутом
состоянии, условием устойчивости ее в
замкнутом состоянии является неохват
а.ф.х.
точки
.
Последнее имеет место, если при частоте,
на которой ![]() ,
фаза
,
фаза ![]() ,
т.е. абсолютное значение фазы меньше
,
т.е. абсолютное значение фазы меньше ![]() .
Сказанное непосредственно следует из
рис. 5.4 а, б. Таким образом,
применительно к логарифмическим
характеристикам, если учесть при этом,
что значению
.
Сказанное непосредственно следует из
рис. 5.4 а, б. Таким образом,
применительно к логарифмическим
характеристикам, если учесть при этом,
что значению ![]() соответствует
соответствует ![]() ,
критерий устойчивости Найквиста
,
критерий устойчивости Найквиста

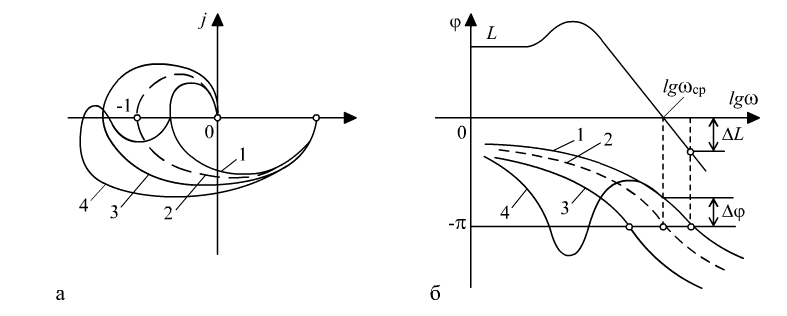 Рис.
5.4. Амплитудно-фазовые и логарифмические
частотные характеристики устойчивых
и неустойчивых САУ
Рис.
5.4. Амплитудно-фазовые и логарифмические
частотные характеристики устойчивых
и неустойчивых САУ