
- •Определение Множества. Элементы. Пустое, универсальное, подмножество. Равенства подмножеств. Множествами и их свойства. Декартово произведение множеств.
- •2. Операции над множествами. Диаграммы Венна.
- •Отношения. Унарные и бинарные, Тождественное и универсальное.
- •5. Отношения. Область определения, значений. Обратное отношение.
- •9. Специальные бинарные отношения:
- •Функция. Инъекции, сюръекции, биекции. Понятие последовательности. Частичная функция.
- •Эквивалентность множеств. Мощности множества. Сравнение мощностей. Типы множеств.
- •Матрицы бинарных отношений и их свойства.
- •11.Булевы алгебры.
- •12. Логические операции, их таблицы истинности.
- •23. Перестановки.
- •14. Эквивалентность формул.
- •36. Планарные графы.
- •27. Определение графа. Виды и способы задания графов.
- •28. Подграфы и части графа. Операции над графами. N-Мерные кубы.
- •Объединение: .
- •29. Маршруты, циклы, цепи. Достижимость и связность (матрицы достижимости, контрдостижимости, связности).
- •21. Теорема Жегалкина. Способы построения полиномов Жегалкина. Линейные функции.
- •41. Фундаментальные циклы, разрезы. Матрицы фундаментальных циклов, разрезов.
- •18.Минимизация днф: метод Квайна
- •13. Булевы функции, способы их задания. Представления булевых функций формулами.
- •15. Дизъюнктивные и конъюнктивные нормальные формы. Алгоритм приведения формулы к днф и кнф.
- •16. Минимизация днф. Сокращенная, тупиковая, минимальная днф.
- •17. Минимизация днф Карты Карно.
- •19. Принцип двойственности. Самодвойственные функции.
- •26. Объекты теории графов. Цели и методы.
- •30. Эйлеровы графы, циклы, цепи. Алгоритм построения эйлерова цикла.
9. Специальные бинарные отношения:
Пусть Р – бинарное
отношение на множестве А:
![]()
Отношение Р
называется рефлексивным,
если для всех
![]() выполняется
выполняется
![]() ,
т.е
,
т.е
![]() .
Отношение Р называется симметричным,
если для любых
.
Отношение Р называется симметричным,
если для любых
![]() из
из
![]() следует
следует
![]() ,
т.е Р-1=Р,
или [P]T=[P].
Отношение Р называется антисимметричным,
если из
и
следует, что x=y,
т.е
,
т.е Р-1=Р,
или [P]T=[P].
Отношение Р называется антисимметричным,
если из
и
следует, что x=y,
т.е
![]() ,
или на языке матриц это означает, что в
матрице
,
или на языке матриц это означает, что в
матрице
![]() все элементы вне главной диагонали
являются нулевыми. Отношение Р называется
транзитивным,
если из
и
все элементы вне главной диагонали
являются нулевыми. Отношение Р называется
транзитивным,
если из
и
![]() следует
следует
![]() ,
т.е
,
т.е
![]()
Функция. Инъекции, сюръекции, биекции. Понятие последовательности. Частичная функция.
Отношение
![]() называется функцией
или отображением
из множества А в множество В, если
называется функцией
или отображением
из множества А в множество В, если
![]() и из (x,y1)
є f,
(x,y2)
є f
следует y1=y2.
Если вместо
и из (x,y1)
є f,
(x,y2)
є f
следует y1=y2.
Если вместо
![]() выполняется
выполняется
![]() ,
то f
называется частичной
функцией.
Функция f
из А в В обозначается через
,
то f
называется частичной
функцией.
Функция f
из А в В обозначается через
![]() или
или
![]() .
Если (x,y)
є f,
то пишем y=f(x)
или
.
Если (x,y)
є f,
то пишем y=f(x)
или
![]() .
Функция
.
Функция
![]() называется разнозначной
инъективной
(инъекцией) или 1-1 функцией
если из условия, что
называется разнозначной
инъективной
(инъекцией) или 1-1 функцией
если из условия, что
![]() выполняется х1≠х2,
следует y1≠y2.
Функция
выполняется х1≠х2,
следует y1≠y2.
Функция
![]() называется функцией из А на В или
сюръекцией,
если
называется функцией из А на В или
сюръекцией,
если
![]() .
Функция
.
Функция
![]() называется взаимно однозначным
соответствием между множествами А и В
или биекцией,
если она инъективна и сюръективна
одновременно.
называется взаимно однозначным
соответствием между множествами А и В
или биекцией,
если она инъективна и сюръективна
одновременно.
Биекция
![]() называется подстановкой.
называется подстановкой.
Утверждения:
Если
 ,
,
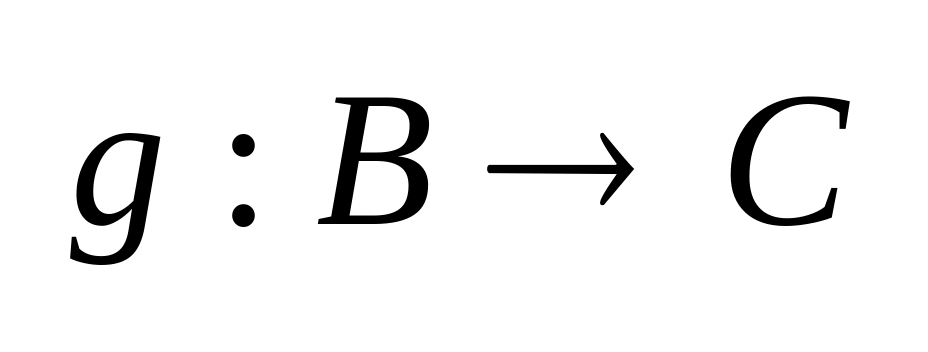 ,
то
,
то

Если
 ,
то
,
то

Если f и g - инъекции, то f•g – инъекция.
Если f,g – сюръекции, то f•g – сюръекция
Если f и g – биекции, то f•g – биекция
Если , то

Функция
![]() называется последовательностью. Её
можно представить в виде f(0)=b0,
f(1)=b1,…,
f(n)=bn.
называется последовательностью. Её
можно представить в виде f(0)=b0,
f(1)=b1,…,
f(n)=bn.
Эквивалентность множеств. Мощности множества. Сравнение мощностей. Типы множеств.
Множества А и В называются эквивалентными (А~В), если существует биекция f: А↔В.
Свойства отношения эквивалентности:
А~А (поскольку idA: А↔А);
если А~В, то В~А (т.к. из f: А↔В следует f-1: В↔А);
если А~В и В~С, то А~С (т.к. из f: А↔В, g: В↔С следует f•g: А↔С).
Мощностью множества А называется класс всех множеств, эквивалентных множеству А (|А|).
Эквивалентные множества А и В называются равномощными: |A|=|B|.
Если А~n
для некоторого
![]() ,
т.е. А имеет ровно n
элементов, то множество А называется
конечным
(|A|=n).
,
т.е. А имеет ровно n
элементов, то множество А называется
конечным
(|A|=n).
Множество, не являющееся конечным, называется бесконечным. Если А~ω, то множество А называется счетным: |A|=ω. Если А~2ω, то множество А называется континуальным или континуумом: |A|=2ω.
Мощности множеств также иногда называют кардинальными числами.
Сравнение мощностей:
Говорят, что мощность множества А не превосходит мощности множества В: |A|≤|B|, если А эквивалентно некоторому подмножеству множества В
Операции над кардинальными числами:
Пусть |A|=α, |B|=β. Тогда
1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
Правило суммы: Если
|A|=m,
|B|=n,
то
![]() .
.
Правило произведения:
Если |A|=m,
|B|=n,
то
![]() .
.
Правило степени: Если |A|=m, |B|=n, то |AB|=mn. .
Мощность булеана:
|P(U)|=2|U| для любого множества U.
Доказательство:
Установим биекцию между Р(U) и 2А
Любому подмножеству
А из U
взаимно однозначно ставим в соответствие
функцию
![]() ,
для которой
,
для которой
![]()
т.е. P(U)~2U. Заметим, что 2|U|=|2U|.
