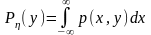15. Основные дискретные распределения случайных величин.

1. Биноминальное распределение.

Схема Бернулли: производится n независимых испытаний в каждом из которых возможно только 2 исхода: P(A)=p, P( )=q, p+q=1

возможное распределение этой величины.

Вероятность этих значений вычисляется по формуле Бернулли. .

Найдем МО и DX

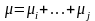, где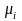 -число появлений события в i-ом (одном) испытании.Закон распределения МО:

	0	1
P	q	p

M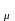 =0*q+1*p=p ; M =np

Чтобы найти дисперсию M ₂=0²*q+1²*p=p

D = M ₂ - (M )²=p-p²=p(1-p)=pq

2. Распределение Пуассона.

Пусть производится n независимых испытаний в каждом из которых вероятность появления события A равна p. Для определения вероятности k пользуется ф. Бернулли. Если вероятность мала, а число испытаний велико то формулой Пуассона. =0,1,...,m

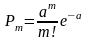
В распределении Пуассона МО и дисперсия равны

3. Геометрическое распределение.

Производится n независимых испытаний в каждом из которых только 2 исхода: P(A)=p, P( )=q, p+q=1

Испытание производится до появления события А

Вероятности этих значений

P_m=q^m-1p

P₃=q²p

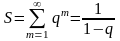
Сходящийся ряд можно почленно дифференцировать: S`=1/(p²)

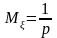
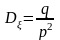
16. Равномерное и показательное распределение.

Относятся к непрерывным случайным величинам.

1. Равномерное распределение.

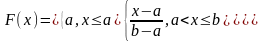
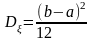
2. Показательное распределение.

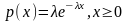
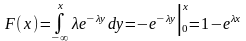
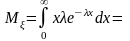
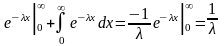
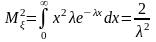
Характерное свойство показательного распределения

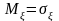
17. Нормальное распределение.

Нормальным (распределением Гаусса) называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью.

Пусть K=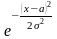 Тогда

Свойства:P(x) – чётная,

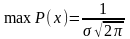
Нормальное распределение определятся 2 параметрами .

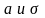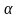– мат ожидание, 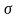- квадратическое отклонение нормального распределения.

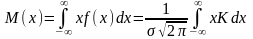
От произвольного нормального к стандартному распределению переходят с помощью формулы .

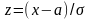Функция стандартного нормального распределения имеет вид.

Часто приводится функция Лапласа (нечетная)

Ф(z)=Ф₀(z)+0,5

18. Двумерная функция распределения и ее свойства.

Многомерная случайная величина Х=(Х₁, Х₂, ... Х_n) – это совокупность случайных величин Х_i , заданных на одном и том же пространстве элементарных событий

Закон распределения вероятностей многомерной случайной величины Х задается ее функцией распределения

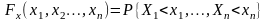
которая является числовой функцией многих переменных и как вероятность принимает значения на отрезке [0,1].

Свойства двумерной функции распределения совпадают со свойствами многомерной функции распределения.

1. Для всех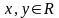 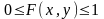, так как это вероятность.

2. F(x,y) –неубывающая функция.

3.

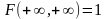
4.

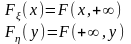
Двумерный дискретный закон распределения изображается в виде таблицы, где в первой строке строчки перечисляются возможные значения случайной величины , в первом столбце возможные значения

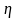
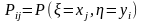
При этом должно выполняться условие нормировки

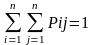
19. Двумерная плотность вероятности и ее свойства.

Случайный вектор 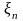называется непрерывным, если существует такая непрерывная неотрицательная функция p(x,y), что для любых x,y R выполняется соотношение

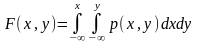
При этом p(x,y) – двухмерная плотность вероятности.

Свойства.

1.

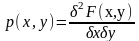
2.

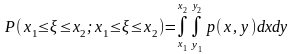
3.

4.