
- •Что такое математическое программирование (мп)?
- •2. Чем отличаются задачи линейного программирования от (злп) от общих задач мп?
- •3. Приведите примеры злп.
- •4.Что такое каноническая форма злп?
- •5. Любую ли злп можно привести к канонической формуле?
- •6. Какие способы решения злп Вы знаете?
- •7. Что такое двойственная задача?
- •8. Каков экономический смысл двойственной задачи?
- •9. Как использовать двойственные оценки для исследования злп?
- •10. Что такое транспортная задача (тз)?
- •11. Каковы способы решения тз?
- •12. Всегда ли может быть решена тз?
- •13. Как сводить тз с открытой моделью и дополнительными условиями к задаче с закрытой модели?
- •14. Какие экономические и управленческие задачи можно интерпретировать как транспортные?
- •15. Как решать задачи целочисленного программирования?
- •16. Как решается задача поиска экстремума для нелинейных функций с ограничениями равенствами?
- •17. Какие задачи рассматриваются в теории динамического программирования?
- •20. Что такое игра с природой?
- •21. Как решать матричные игры?
- •22. Каковы основные критерии решения игр с природой?
- •23. Что такое матрица рисков?
- •24. Какие статические модели экономики Вы знаете?
- •25. Что такое динамического равновесие в экономике?
7. Что такое двойственная задача?
Двойственная задача - это вспомогательная задача линейного программирования, формулируемая с помощью определенных правил непосредственно из условий исходной, или прямой задачи, которая применима к любой форме представления прямой задачи. В основу такого подхода положен тот факт, что использование симплекс-метода требует приведения любой ЗЛП к каноническому вид.
8. Каков экономический смысл двойственной задачи?
В плановом периоде появились отходы сырья m видов в объемахединиц . Из этих отходов, учитывая специализацию предприятия, можно наладить выпуск n видов неосновной продукции. Обозначим через норму расхода сырья i-го вида на единицу j-й продукции, - цена реализации единицы j-й продукции (реализация обеспечена). Неизвестные величины задачи: -- объемы выпуска j-й продукции, обеспечивающие предприятию максимум выручки.
Д. з. состоит в минимизации затрат при заданных лимитах ресурсов и формулируется следующим образом (в обозначениях, приведенных в ст. “Линейное программирование”):
Найти набор переменных v1, v2, ..., vn (называемых разрешающими множителями, объективно обусловленными (оптимальными) оценками, двойственными ценами и т. п.), минимизирующий линейную функцию
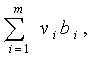
при том условии, что каждый включенный в план вид продукции рентабелен (полученная продукция оправдывает затраты), а невключенные в план — не более рентабельны, чем первые.
Оценки характеризуют влияние свободных членов ограничений прямой задачи на оптимальную величину целевой функции. Иначе говоря, они показывают относительный вклад каждого ресурса в достижение оптимума; небольшое изменение количества ресурса изменяет оптимальное значение пропорционально величине оценки.
9. Как использовать двойственные оценки для исследования злп?
Любую задачу максимизации с экономической точки зрения можно рассматривать как задачу о распределении ограниченных ресурсов b1, b2,…, bn между различными потребителями, например, между некоторыми технологическими процессами, которые представляются столбцами A1, А2, ..., Аm матрицы ограничений задачи. Любое допустимое решение задачи линейного программирования х1, х2, ..., хm дает конкретное распределение, указывающее ту долю каждого из ресурсов, которая должна быть использована при осуществлении соответствующего технологического процесса.
Понятие двойственности рассмотрим на примере задачи оптимального использования сырья. Пусть на предприятии решили рационально использовать отходы основного производства. В плановом периоде появились отходы сырья m видов в объемахединиц . Из этих отходов, учитывая специализацию предприятия, можно наладить выпуск n видов неосновной продукции. Обозначим через норму расхода сырья i-го вида на единицу j-й продукции, - цена реализации единицы j-й продукции (реализация обеспечена). Неизвестные величины задачи: -- объемы выпуска j-й продукции, обеспечивающие предприятию максимум выручки.
10. Что такое транспортная задача (тз)?
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.[1][2] Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки.
