49.Применение уравнения Шрёдингера к частице в потенциальном ящике. Уровни энергии и волновые функции микрочастицы.

Потенциальный ящик – обл.одномернонго пространства, огр. 2мя бесконечными барьерами, за которые не может проникать ни классическая, ни квантовая частица.

Учитывая, что p=h/ λ и 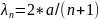, то получим 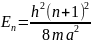, n=0,1,2,…. Энергия движ.частицы может меняться только дискретно. Значения этой энергии называются энергетическими уровнями. Энергия квант.част. не может быть = 0

К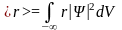 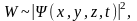онкретный вид волновой функции определяется внешними условиями, в которых находится микрочастица. Волновая функция (или Ψ-функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:

1 формула - где |Ψ|²=ΨΨ` , где Ψ` – функция комплексно-сопряженная с Ψ.

Т.е., описание микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени в области с координатами x и dx, y и dy, z и dz.

Волновая функция Ψ является основной характеристикой состояния микрообъектов.

2 форула - Например, среднее расстояние <r> электрона от ядра вычисляется по формуле

Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями Ψ₁, Ψ₂, … Ψ_n, то она может находиться в состоянии, описываемом линейной комбинацией этих функций

52.Спин электрона. Квантование собственного момента импульса электрона. Спиновое квантовое число. Квантование проекции спина электрона. Магнитное спиновое квантовое число. Опыты Штерна и Герлаха.

Спин— собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.

Спин квантуется по закону 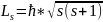, где s – спиновое квантовое число. По аналогии с орбитальным моментом импульса, проекция 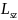спина квантуется так, что вектор 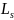может принимать 2s+1 ориентации. Так как в опытах Штерна и Герлаха наблюдались только 2 ориентации, то 2s+1=2, откуда s=1/2. Проекция спина на направление внешнего м.п: . Опытные данные привели к необходимости характеризовать микрочастицы добавочной внутренней степенью свободы.

Опыт подтвердил наличие у атомов спина и факт пространственного квантования направления их магнитных моментов. Опыт: пучок атомов серебра пропускали через сильно неоднородное магнитное поле, от сильного постоянного магнита. Когда атомы проходили через поле, на них действовала сила м.п, отклонявшая летящие между магнитами атомы от их направления движения. На пластинке образовались две чёткие узкие полосы, что говорило о том, что магнитные моменты атомов вдоль выделенного направления только два значения, это подтверждало предположение квантово-механической теории о квантовании магнитного момента атомов.

Позднее с такими же результатами были проделаны опыты для пучков атомов других металлов, пучков протонов и электронов.