32)Физический смысл пси-функции. Физический смысл волновой функции

В координатном представлении волновая функция зависит от координат (или обобщённых координат) системы. Физический смысл приписывается квадрату её модуля , который интерпретируется как плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами в момент времени :

.

Тогда в заданном квантовом состоянии системы, описываемом волновой функцией , можно рассчитать вероятность того, что частица будет обнаружена в любой области пространства конечного объема :       .

Следует также отметить, что возможно измерение и разницы фаз волновой функции, например, в опыте Ааронова — Бома.

33)Квантование энергии (частица в потенциальной яме). Бесконечно глубокая потенциальная яма.

Н айдем собственные значения энергии и соответствующие им собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Предположим, что частица может двигаться только вдоль оси х. Пусть движение ограничено непроницаемыми для частицы стенкам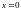и и . Потенциальная энергия в таком случае имеет следующий вид:

Рассмотрим отдельно области I, II, III. В областях II и III уравнение Шредингера выглядит следующим образом:

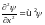
Из курса дифференциальных уравнений известно, что решение следует искать в виде:

.

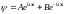Для зоны II соответственно:

,

где из условия нормировки следует, что , поскольку при 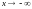, (для зоны II ), и при отличном от нуля - функция не будет нормирована, ее площадь будет уходить в бесконечность. Значит

,

где 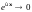, поскольку , и .

В области II убывает с уменьшением х тем быстрее, чем больше 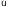. При , и получается, что частица не может находиться в области II, т.к. в области II, а 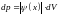- вероятность нахождения частицы.

Аналогично в области III .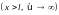

Итак, за пределами бесконечно глубокой потенциальной ямы частица находиться не может (это нереальный пример, но очень важный).

Рассмотрим область I.

.

С учетом того, что в этой области потенциальная энергия частицы = 0, запишем:

,

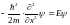
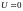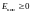учтем, что т.к. , а , т.о. , тогда мы снова пришли к дифференциальному уравнению, решение которого нам хорошо известно:

.

Т.к. волновая функция в области I тождественно равна нулю, из ее непрерывности следует:

.

Это равенство следует из двух следующих граничных условий:

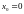
1) т.к. при 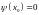, (а не );

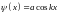2) т.к. при , имеем:

,

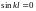
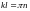причем 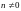, 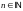т.к. получится, что частицы нет ни внутри ямы, ни за ее пределами.

Вспоминаем, что

,

подставляя это достижение в , получим:

.

Энергия частицы может принимать только дискретный ряд значений. Значит, волновая функция в области I имеет вид:

.

Найдем константу . Из условий нормировки – это некоторая константа:

Таким образом, собственные функции имеют вид:

.

Изобразим графики собственных функций 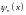и графики плотности вероятности обнаружения частицы на различных расстояниях от стенок ямы :

В состоянии n = 2 частица не может находиться в центре ямы, а при n = 1 – вероятность нахождения частицы в центре ямы максимальна. В состояниях с большими n число нулей и максимумов будет велико. Если размеры детектора будут больше периода 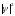, то вероятность обнаружения частицы в яме будет одинакова во всех точках, т.е. свойства системы в случаях больших n аналогична классической теории.