14. Прямая Эйлера

Т 1. Пусть О — центр окружности, описанной около треуголь­ника ABC, М — точка пересечения его медиан, Н — орто­центр. Тогда точки О, М, Н лежат на одной прямой, причем М делит отрезок ОН в отношении 2:1, считая от Н. Прямая, содержащая эти точки, называется прямой Эйлера для треугольника ABC. Дано: ∆АВС, ВB₁┴АС, СС₁ ┴АВ, Н = ВB₁∩ СС₁, АА₂, ВВ₂ — медианы ∆АВС, М = АА₂ ∩ВВ₂. В₂О┴АС, А₂О┴ВС, О = В₂О ∩ А₂О (см. рис.). Доказать: М ОН, МН=2ОМ.

Доказательство. Пусть М₁, = ОН∩ВВ₂.

Тогда ∆М₁ОВ₂ ~ ∆M₁HB , так как OM_lB₂ = HM₁B (как вертикаль­ные), OB₂M₁ = M₁BH (как накрест лежащие при параллельных прямых ОВ₂ и ВВ₁ и секущей В₂В ). Из подобия треугольников ОМ₁В₂ и НМ₁В получаем: . Отношение ОВ₂: ВН = 1:2, так как расстояние от центра описанного круга О до стороны ВС вдвое меньше, чем расстояние от вершины В до ортоцентра Н. Тогда из (1) получаем . Но если медиана делится точкой в отношении 2:1, считая от верши­ны треугольника, то это точка — центроид треугольника, т.е. точка совпадает с точкой М. А это означает, что точки Н М, О лежат на одной прямой, так как точкой М₁ мы обозначили точку пересече­ния ОН с медианой ВВ₂.Из (1) имеем _.Так как = М , то 

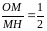
15. Окружность Эйлера

Т еорема 6.14. В любом треугольнике основания высот, середины сторон и середины отрезков, соединяющих ортоцентр с вершина­ми, лежат на одной окружности.

Окружность носит название окружности девяти точек или окружно­сти Эйлера.

Дано: АВС, А1 — середина ВС, В1 — середина АС, С1 — середина АВ, ВН₂ перпендик. АС, Н₂€АС, АН₁перпенд.ВС, H1,€ВС, СН₃перп.АВ, H₃ €АВ, АH1пересеч. ВH₂ и с СH₃ = Н , А₂ — середина АH, В₂ — середина ВH, С₂ — середина СH (рис. 6.11). Доказать: А1, В1, С1, H1, H₂, H₃, A2, В₂, С₂ — лежат на окружности.

Доказательство.

1) Рассмотрим четырехугольник A2C1A1C2. С1А1 — средняя линия ∆АВС .Значит, С1А1 || АС и С1A1 = 1/2АС ;

А ₂С₂ — средняя линия ∆АНС .Значит, С₂A2|| АС и С2A2 = 1/2 АС . Следовательно, А₂С₁А₁С₂ —параллелограмм.

2. C1,A2 — средняя линия ∆АВH . Значит, С1A2 || ВH . Следовательно, С1A2 1 A2C2 , так как А₂С₂|| АС.

3. Таким образом, С₁А₂С₂А₁ — прямоугольник. Тогда существует ок­ружность, диаметром которой является отрезок С1С₂ (т. е. точка Е— середина С1С₂ — ее центр), которой принадлежат точки А₂, С1, А1, С₂.

4. С₁В₂С₂В1— прямоугольник, так как:

а) С1В1 — средняя линия ∆АВС . Значит, С1В1 || ВС и С1В1 = 1/2ВС.

б) С₂В₂ — средняя линия ∆ВHС . Значит, С₂В₂|| С В и С₂В₂ = 1/2СВ .

в) С1В₂перп.В₂С₂, так как С1В₂|| АH и В₂С₂|| АН .

5) С1С₂ — диаметр окружности (центр окружности Е), описанной около прямоугольника В₁С₁В₂С₂. Таким образом, точки С, В₂, Д, С₂, В1, А2 принадлежат окружности с центром Е и диаметром С,С₂.

6) E— середина диагонали С,С₂ прямоугольников С,A2С₂A1 и С₁В₁С₂В₁. Значит, и вторые диагонали A1А2 и В,В₂ соответственно прямоугольников С,A2С₂A1 и С₁В₂С₂В₁ проходят через точку Е, так как диагонали прямоугольника равны и точкой пересечения делятся пополам. Значит, A1A2 и В,В₂ —тоже диаметры этой окружности.

7) УГОЛ B₂H₂B 1= 90°, так как ВН₂перп. А С, и этот угол опирается на диаметр В₂В, окружности с центром Е. Значит, Н₂ лежит на окружности.

Аналогично угол А2H1A1 = 90° и A1A2 — диаметр окружности. Значит, точ­ка H, лежит на окружности. уголC₁H₃C₂ = 90° и С,С₂ — диаметр окруж­ности. Следовательно, точка H₃ принадлежит окружности. Таким образом, все девять точек лежат на окружности. Теорема доказана.

Tеорема 6.15. Центр Е окружности девяти точек треугольника лежит на середине отрезка ОН, где Н — ортоцентр треугольника, О — центр описанной окружности, а радиус окружности девяти точек равен половине радиуса описанной около треугольника окружности

Теорема 6.16. Расстояние между центрами О и I описанной и вписанной окружностей треугольника и радиусы R и .r этих окружно­стей связаны формулой: OI² = R² - 2Rr, называемой фор­мулой Эйлера.