9.Метрические соотношения в окружности. Свойства хорд

Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном рассто­янии от данной точки, называемой центром окружности. Отрезок, со­единяющий центр с какой-либо точкой окружности, называется радиу­сом окружности.

Отрезок, соединяющий две точки окружности, называ­ется ее хордой.

Если на окружности взять две точки, то они разобьют окружность на две части, каждая из которых называется дугой окруж­ности, а данные точки — концами этих дуг.

Дуга называется полуокружностью, если отрезок, со­единяющий ее концы, является диаметром окружности. Часть плоскости, ограниченная окружностью, называется кругом.

Кругом с центром О и радиусом R называется фигура, которая состоит из всех точек плоскости, удаленных от точки О не боль­ше, чем на расстояние R.

Свойства хорд

Т1. Диаметр перпендикулярен хорде, не являющейся диамет­ром, тогда и только тогда, когда он проходит через середи­ну хорды. Дано: CD — диаметр окружнос­ти О, АВ — хорда окружности О. CD ∩ АВ = М , AM = MB. Доказать: CD ┴ АВ . Доказательство. Треугольник АОВ равнобедренный (OA = OB как радиусы окружности), ОМ — его медиана. Значит, ОМ — высота треугольника, т. е. ОМ ┴ АВ, или диаметр CD перпендикулярен хорде АВ. Докажем обратное.

Дано: CD — диаметр окружно­сти О, АВ — хорда окружности О, М = AB∩CD, CD ┴ АВ. Доказать: AM = MB. Доказательство. Треугольник АОВ равнобедренный (OA = OB) и ОМ — его высота, а значит, ОМ — медиана, т. е. AM= MB. 

Следствие. Расстояние от центра окружности до хорды равно расстоя­нию от центра до середины хорды.

Т2. Хорды одной окружности равны тогда и только тогда, когда они равноудалены от центра. Дано: окружность О, CD — хорда окружности О, АВ — хорда окружности О, АВ = CD. М— середина АВ, N— середина CD. Доказать: ОМ = ON. Доказательство. ∆OND = ∆ОМВ, так как они прямоугольные (ON ┴CD и ОМ┴АВ), ND= MB как половины отрезков CD и АВ, и OD = ОВ как радиусы окружности. Из равенства треугольников OND и ОМВ следует равенство их катетов ON и ОМ. Докажем обратное. Дано: окружность О, АВ и CD — ее хорды, ON┴CD, т. е. N— середина CD, М— середина АВ, т. е. ОМ ┴ АВ , ОМ= ON. Доказать: АВ = CD. Доказательство. ∆OND = ∆OMB, так как они прямоугольные ( OND = OMB = 90°), ON = ОМ (по условию) и OD = ОВ (радиусы окружности О). Из равен­ства треугольников OND и ОМВ следует равенство их катетов ND и MB. Значит, CD = 2ND = 2MB = АВ. 

Опр..Угол, вершина которого лежит в центре окружности, называется центральным углом.

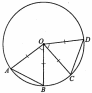
Если две хорды АВ и KL пересекаются в точке М, то справедливо равенство: АМ*МВ=КМ*ML=R²-d²

Т3. Хорды данной окружности равны тогда и только тогда, ког­да они стягивают равные дуги. Доказательство: Равенство хорд АВ и CD следует из равенства треугольников АОВ и COD (по двум сторонам и углу между ними). Обратно: Дано: окр. О, АВ и CD — хорды окружности О, АВ=СD. Доказать: AOB= COD.

Д-во: Равенство углов АОВ и COD следует из равенства треугольников АОВ и COD (по трем сторонам).Эта теорема может быть сформулирована и таким образом: равные хорды видны из центра окружности под равными углами, и наоборот, под равными углами из центра окружности видны равные хорды. Т4. Дуги, заключенные между параллельными хордами окружности, равны. Док-во: Равенство дуг АС и BD непосред­ственно следует из равенства уг­лов ABC и BCD. (см. рис. Справа ------>------>------>------>------>------>------>) 