Функциональные методы

4. Использование ограниченности функций.

Некоторые уравнения 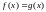таковы, что при любом значении из области его определения левая и правая части уравнения удовлетворяют условиям 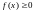и 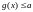соответственно, где 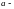некоторое число. Тогда решение уравнения сводится к нахождению значений , для которых одновременно и .

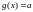Если же хотя бы одно из неравенств строго, то исходное уравнение не имеет решений.

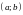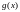5. Использование монотонности функций. Если на некотором промежутке функции и , входящие в уравнение таковы, что непрерывна и возрастает, а непрерывна и убывает, то равенство возможно только при единственном значении , которое и является корнем данного уравнения на рассматриваемом промежутке. Иногда этот корень можно найти подбором.

6. Графический метод. Иногда полезно рассмотреть эскизы графиков функций и , входящих в уравнение . Этот метод, не являющийся строгим решением, может помочь установить: а) существуют ли у данного уравнения корни и сколько их; б) на какие множества следует разбить область определения уравнения, чтобы на каждом из этих множеств использовать свой способ решения.

2. Рациональные неравенства и методы их решения

Пусть f(x)=0 числовая функция одной или нескольких переменных (аргументов). Решить неравенство f(x) < 0 (f(x) > 0) (1) - это значит найти все значения аргумента (аргументов) функции, при которых неравенство (1) справедливо. Множество всех значении аргумента (аргументов) функции, при которых неравенство (1) справедливо, называется множеством решении неравенства или просто решением неравенства.

Два неравенства считаются эквивалентными, если множества их решении совпадают.

Под множеством допустимых значений неизвестных, входящих в неравенство, понимают область определения функции f(x)=0.

Алгебраические неравенства.

Линейными (строгими и нестрогими) называются неравенства вида

ax + b > 0, ax + b < 0 (ax + b>=0, ax + b<=0)

Квадратными (строгими и нестрогими) называются неравенства вида

ax² + bx + c > 0, ax² + bx + c < 0,

ax² + bx + c >= 0, ax² + bx + c <= 0, где a, b, c – некоторые действительные числа и а ≠ 0.

Квадратное неравенство ax² + bx + c > 0 в зависимости от значения своих коэффициентов a, b и c имеет решения:

при а > 0 и D = b² – 4ac ≠0 , то х принадлежит интервалу

при а > 0 и D < 0 x – любое действительное число;

при а < 0 и D ≠0 x(( –х₁ ; ;х₁ ) );

при а < 0 и D < 0 x = ( (т. е. решении нет ).

Решение неравенства ax² + bx + c < 0 сводится к решению рассмотренного неравенства, если обе части неравенства умножить на (–1).

Метод интервалов.(основной метод)

Находим область определения функции, затем отмечаем в этой области нули функции, которые разбивают область определения на несколько промежутков, внутри каждого из которых функция определена, непрерывна и сохраняет знак. Для определения знака функции на конкретном промежутке находим знак в любой (удобной) точке этого промежутка.

Дробно–рациональные неравенства.

Решение рационального неравенства Pn(x)/Qn(x) > 0 (5) где Рn(х) и Qm(х) (многочлены, сводится к решению эквивалентного неравенства (4) следующим образом: умножив обе части неравенства (5) на многочлен [Qm(x)]2, который положителен при всех допустимых значениях неизвестного х (т.е. при тех х, при которых Qm(x) ( 0), получим неравенство Рn(х) ( Qm(x) > 0, эквивалентное неравенству (5).

ГРАФИЧЕСКОЕ РЕШЕНИЕ НЕРАВЕНСТВ

Неравенства с одной или двумя переменными можно решать графически.

Неравенство с одной переменой можно записать так: f(x) > g(x), где f(x) и g(x) – выражения, содержащие переменную.

Построим в одной системе координат графики функций y = f(x) и у = g(x).

Решение неравенства с двумя переменными f(x,y)>0 есть множество точек плоскости, координаты которых удовлетворяют этому неравенству. Рассмотрим на примерах решение некоторых неравенств с двумя переменными.