2.3. Кодирование и модуляция

В вычислительной технике в настоящее время практически всегда применяются двоичная система счисления (цифры) и дискретные сигналы, в то время как, в телекоммуникационных системах по историческим причинам, пока что, часто используются аналоговые сигналы.

При передаче дискретных данных по цифровым линиям связи используется линейное кодирование информации. Существует множество способов кодирования, например:

• потенциальный способ, где двоичной единице соответствует один уровень напряжения, а двоичному нулю – другой;

• импульсный способ, где представление двоичных цифр осуществляется импульсами различной полярности.

Отметим, что при передаче информации по цифровой линии связи изменение сигнала происходит через фиксированный интервал времени – такт. В начале каждого такта на вход приемника поступает новая информация, даже если уровень потенциала на входе не изменялся. Например, пусть такт составляет 0,2с, и сигналу «единица» соответствует амплитуда 3 В. Тогда, если на входе приемника присутствует потенциал 3В в течение 4 с, то это значит, на вход приемника поступило 20 единичных сигналов.

В аналоговых линиях связи для передачи непрерывных сигналов используется так называемый несущий сигнал - синусоиду (непрерывный сигнал постоянной частоты, которая называется несущей частотой). Передача дискретных данных по этим линиям осуществляется изменением (модуляцией) характеристик несущего сигнала.

Один из постулатов теории информации гласит - любое различимое непредсказуемое изменение сигнала несет в себе информацию. Поэтому как постоянная тактовая частота (используемая при кодировании), так и идеальная бесконечная синусоида (используемая при модуляции) сами по себе никакой информации не несут. Для кодирования и модуляции дискретных данных используется изменение параметров периодического сигнала. В случае последовательности импульсов – это изменение знака импульсов или частоты их следования, а для синусоиды – это изменение ее частоты, амплитуды и фазы (по отдельности, или в некоторой комбинации).

Рис. 2.3.1 иллюстрирует основные методы кодирования и модуляции дискретных данных. Подробная информация о видах модуляции сигналов и методах кодирования данных содержится в п. 8 данного пособия.

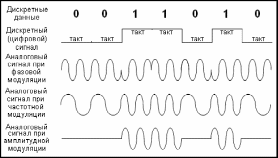
Рис. 2.3.1 Методы кодирования и модуляции дискретных данных

2.3.1.Скорость передачи, искажение и затухание сигнала

Для измерения количества изменений информационного параметра в единицу времени используется особая единица, бод. Иначе говоря, 1 бод = 1 изменение информационного параметра в секунду. Скорость же передачи информации измеряется в бит/с, и, в общем случае, она не равна скорости передачи в бодах. Это зависит от числа состояний сигнала в такте. Например, если различается число состояний сигнала по фазе – 0, π/2, ¾ π, π, для каждого из двух значений амплитуды, тогда информационный сигнал может иметь 8 состояний, и любое состояние несет информацию 3 бит, т.е. здесь 1 бод = 3 бит. В другом случае, когда единица кодируется импульсом положительной полярности, а ноль – импульсом отрицательной полярности, то есть физический сигнал дважды изменяет свое состояние для передачи 1 бит, получаем 2 бод = 1 бит.

Обычно сигнал имеет только 2 физических состояния и 1 бод = 1 бит.

Согласно теории гармонических колебаний – любой гармонический процесс можно представить в виде суммы синусоидальных колебаний различной частоты и амплитуды, это - так называемое разложение Фурье (см. Приложение). Каждая составляющая этой суммы называется гармоникой. Набор всех гармоник – называется спектральным разложением или спектром исходного сигнала.

Шириной спектра называется разность между максимальной и минимальной частотами спектра на конкретно заданном уровне амплитуды сигнала.

Непериодические, импульсные сигналы можно представить в виде интеграла от спектра распределения. Произвольный импульс можно представить с помощью симметричной единичной импульсной функции, которую еще называют дельта-функцией Дирака. Это функция, описывающая идеальный импульс нулевой длительности, которая определяется следующим образом:

δ(t-t_o) = ∞ в точке t = t_o; и δ(t-t_o) = 0 при t ≠ t_o и при этом,

Тогда последовательность прямоугольных импульсов можно представить как набор интегралов Фурье, вида:

то есть бесконечной суммой тригонометрических рядов гармонических функций. Причем амплитуды высших гармоник довольно быстро убывают, так что, начиная с некоторых высших членов ряда, их вклад в конечную функцию можно не учитывать. А это означает, что можно не рассматривать распространение и влияние высших гармоник сигнала в среде. Но, при этом изменение амплитуды какой-либо, вносящей заметный вклад, гармоники в линии передачи может привести к искажению формы и изменению общей амплитуды сигнала. Форма сигнала искажается, когда различные гармоники искажаются неодинаково, это явление называют дисперсией частот.

Идеальная передающая среда не вносит помех в сигнал, и не имеет сопротивления. В реальности же сигнал может искажаться вследствие влияния электромагнитных помех (шумов). Его амплитуда уменьшается из-за наличия потерь на омическом сопротивлении линии. Кроме того, величины емкостного и индуктивного сопротивлений реальных линий связи имеют ненулевые значения. Вследствие чего различные гармоники искажаются по-разному, и итоговый сигнал искажается по форме. В частности, из-за дисперсии частот первоначально прямоугольные импульсы дискретных сигналов расплываются и сглаживаются. Подробнее о сопротивлении передающей среды будет сказано при рассмотрении характеристик физических каналов, п.2.5.

Основными достоинством современной цифровой передачи данных по сравнению с традиционной аналоговой, является ее меньшая подверженность воздействию шумов, а, следовательно, и большая сопротивляемость к возможному искажению передаваемой информации. Основным же недостатком цифровой передачи по сравнению с аналоговой - является более быстрое затухание сигнала¹ при его продвижении в передающей среде. При этом затухание дискретного сигнала усиливается как при увеличении расстояния, так и при увеличении частоты следования двоичных импульсов напряжения.

Для устранения затухания сигнала в цифровых линиях связи используются специальные устройства - повторители, которые, получив затухающий сигнал, распознают содержащиеся в нем данные и передают далее по линии восстановленный по форме и усиленный сигнал. Повторители выгодно отличаются от применяемых в традиционных аналоговых линиях устройств - усилителей, которые просто усиливают передаваемый сигнал. Простое усиление сигнала увеличивает и наложенные на него компоненты шума. В этом случае, при прохождении значительного расстояния через каскад усилителей, смысловое содержание сигнала все более и более теряется. Поэтому в современных системах передачи дискретных данных по аналоговым линиям используются аналоги устройств-повторителей, которые извлекают из полученного непрерывного сигнала дискретные данные, а затем генерируют и передают далее восстановленный и очищенный от шумов аналоговый сигнал.