9.6. Настройка точки доступа

Точка доступа в беспроводной сети обычно выполняет несколько функций одновременно. Как отмечалось выше, она является своеобразным сервером для узлов - участников беспроводной сети.

Обычно точка доступа физически присоединена кабелем к локальной сети для обеспечения связи между проводным и беспроводным сегментами сети, и таким образом одновременно работает как роутер или как мост.

Поскольку, чаще всего участникам беспроводной сети необходимо обеспечить доступ к Интернет, точка доступа служит также Интернет-сервером для узлов беспроводной сети.

И наконец для того чтобы повысить безопасность всех сегментов сети важной функцией точки доступа является функция брандмауера (файрволла). Эта функция может выполняться, как указывалось выше, аппаратно или программно. В состав точек доступа обычно включают именно аппаратную часть для выполнения защитной функции файрволла.

Необходимо также, как отмечалось выше, правильно настроить аутентификацию узлов сети и метод шифрования сообщений, ни в коем случае не оставляя установки настроек точки доступа по умолчанию.

Точки доступа обычно поддерживают протокол DHCP (т.е. динамическое назначение IP адресов) и трансляцию сетевых адресов (NAT). Клиенты беспроводной сети получают адреса из числа разрешенных, согласно стандарту RFC-1918 (см. выше п. 3.6.2.). Таким образом, если несколько беспроводных виртуальных сетей подключаются к одной локальной сети – существует опасность возникновения конфликта адресов из-за дублирования, что может привести к неработоспособности сети. При настройке точек доступа необходимо учитывать возможность такого конфликта, и по возможности разделять различные сегменты, например, при помощи введения масок сети.

5. Приложение

Ряды Фурье и интегралы Фурье – используются для представления произвольных функций в виде бесконечных рядов или интегралов.

Разложение Фурье – частный случай разложения в ряд по ортогональным функциям.

Если задан интервал разложения –π < t < π , то ряд Φ, порожденный действительной функцией f(t), для которой существует интеграл 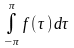, есть бесконечный тригонометрический ряд:

где:

, , ,

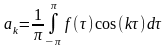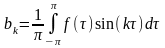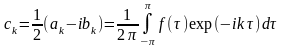k= 0,1,2,3….., и - действительные числа, - комплексное число.

Если задан интервал разложения T,: 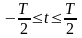, то ряд Φ для действительной функции f(t), для которой существует интеграл , есть бесконечный тригонометрический ряд:

,

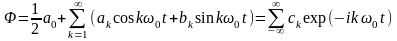ω₀ = 2π/T , где

, ,

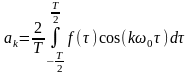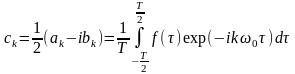
Ряд Φурье для нечетной функции сводится к ряду по синусам, а для четной функции – к ряду по косинусам.

Важное для нас следствие:

Если α(е) – действительная периодическая функция с периодом T, то ее можно представить в виде суммы постоянного члена 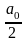и некоторого множества синусоидальных членов со следующими частотами:

– основная частота,

- вторая гармоническая частота, или вторая гармоника;

- третья гармоника и т.д.

Согласно теореме Римана-Лебега, коэффициенты ряда Фурье и - стремятся к нулю при увеличении k (т.е. при k→ ∞), то есть этот ряд сходится.

Следовательно, что важно для нашего рассмотрения, члены ряда с высшими гармониками достаточно малы, и их вклад можно не рассматривать.