
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
Рассмотрим
ограниченную связную обл DϵRnс
граничной поверхностью Г=∂D,
охватывающей облD.
Пусть для определенности Г
.
В обл D
зададим эллиптическое ур-ие 2ого порядка
с достаточно гладкими коэффициентами:L(u)=
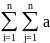 ij(
ij(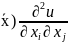 +
+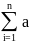 i(
i(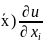 +a(
+a(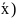 =f(
(16),где
=f(
(16),где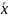 =(x1,x2,..,xn)
D.Потребуем,
чтобы искомая ф-ия u
на границе Г:u(
=(x1,x2,..,xn)
D.Потребуем,
чтобы искомая ф-ия u
на границе Г:u(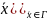 =φ(
=φ(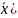 ,
где
φ(
-заданная
ф-ия на поверхности Г.Задача
Дирихле.L(u)=f(
(17)в
облD, u(
=φ(
(18),где
D-ограниче обл.Требуется
найти ф-ию u
(D)
,
которая удовлетворяет ур-нию (17) в обл
D и граничн. условию (18) на граничной
поверхности Г. Задача Дирихле наз-ся
также 1ой краевой задачей. Рассмотрим
частный случай задачи(17),(18),когда
ур-ние (17) является ур-ием Пуассона в
3-ном пространстве R3с
координатами x,y,z, а обл D
,
где
φ(
-заданная
ф-ия на поверхности Г.Задача
Дирихле.L(u)=f(
(17)в
облD, u(
=φ(
(18),где
D-ограниче обл.Требуется
найти ф-ию u
(D)
,
которая удовлетворяет ур-нию (17) в обл
D и граничн. условию (18) на граничной
поверхности Г. Задача Дирихле наз-ся
также 1ой краевой задачей. Рассмотрим
частный случай задачи(17),(18),когда
ур-ние (17) является ур-ием Пуассона в
3-ном пространстве R3с
координатами x,y,z, а обл D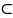 R3.
Внутренняя
задача Дирихле.Δu
R3.
Внутренняя
задача Дирихле.Δu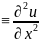 +
+
+
+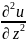 =f(x,y,z)
в обл D,(19)
u(P
=f(x,y,z)
в обл D,(19)
u(P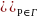 =φ(P),(20)где
D–ограниченная
обл. Решение u(M)=u(x,y,z)
=φ(P),(20)где
D–ограниченная
обл. Решение u(M)=u(x,y,z)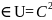 (D)
(D)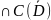 ,наз-ся
классическим
решением
задачи (19),(20).
,наз-ся
классическим
решением
задачи (19),(20).
Корректность
задачи (19),(20),состоящей в следующем:
требуется выделить пространство V
граничных ф-ий φ,для
котрых решение задачи
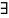 ,
единственно в пространстве U
и непрерывно зависит от граничных
ф-ий. Наиболее просто решаются вопросы
о единственности и непрерывной
зависимости.Т.1.Если
решение u
(D)
задачи
Дирихле(19),(20) существует, тогда оно
единственно в пространстве u.Т.2.Решение
задачи Дирихле (19),(20),в предположении
его существования в прост-ве
U,непрерывно
зависит от граничных ф-ий φ.Т.Шаудера.Пусть
в ур-ии (16) коэфициенты аij(
,аi(
,а(x),
f(
,
единственно в пространстве U
и непрерывно зависит от граничных
ф-ий. Наиболее просто решаются вопросы
о единственности и непрерывной
зависимости.Т.1.Если
решение u
(D)
задачи
Дирихле(19),(20) существует, тогда оно
единственно в пространстве u.Т.2.Решение
задачи Дирихле (19),(20),в предположении
его существования в прост-ве
U,непрерывно
зависит от граничных ф-ий φ.Т.Шаудера.Пусть
в ур-ии (16) коэфициенты аij(
,аi(
,а(x),
f(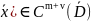 ,m≥0,a(x)≤0,
граничная поверхность Г
,m≥0,a(x)≤0,
граничная поверхность Г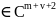 ,
граничная ф-ия φ(
,
граничная ф-ия φ(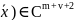 (Г).
Пусть выполнено неравенство равномерной
эллиптичности ур-ия (17):
(Г).
Пусть выполнено неравенство равномерной
эллиптичности ур-ия (17):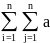 ij(
ij(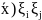 ≥C
≥C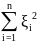 ,
C>0,
тогда
единственное решение задачи (17),(18)
u
,
C>0,
тогда
единственное решение задачи (17),(18)
u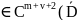 ).
Из теорем следует,что в пространствах
U
и V
задача Дирихле (19),(20) для ур-ия Пуассона
поставлена корректно.
).
Из теорем следует,что в пространствах
U
и V
задача Дирихле (19),(20) для ур-ия Пуассона
поставлена корректно.
Рассмотрим
обл D’=R3,внешнюю
по отношению к
ограниченной обл D
R3,
наложим условия u(M)->0
при M->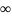 .
Внешняя
задача Дирихле в R3.
Δu=f(x,y,z)(22)в
облD’,
u(P
.
Внешняя
задача Дирихле в R3.
Δu=f(x,y,z)(22)в
облD’,
u(P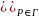 =φ(P)(23),u(M)=>0
при M->
(24).Требуется
найти ф-ию u
=φ(P)(23),u(M)=>0
при M->
(24).Требуется
найти ф-ию u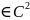 (D’)
(D’)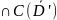 ,
которая удовлетворяет ур-ию (22) в облD’,
граничному усл (23) и равномерно->0 на
бесконечности.
Задача Неймана для ур-ия Пуассона.Рассмотрим
ограниченную обл D
R3с
границей Г
.Для
обл D
поставим краевую задачу для уравнения
Пуассона, когда на поверхности Г задана
производная функции u.
Внутренняя
задача Неймана.
Δu=f(x,y,z)
в D,
f
,
которая удовлетворяет ур-ию (22) в облD’,
граничному усл (23) и равномерно->0 на
бесконечности.
Задача Неймана для ур-ия Пуассона.Рассмотрим
ограниченную обл D
R3с
границей Г
.Для
обл D
поставим краевую задачу для уравнения
Пуассона, когда на поверхности Г задана
производная функции u.
Внутренняя
задача Неймана.
Δu=f(x,y,z)
в D,
f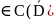 ,(25)
,(25)
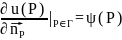 ,ψ
,ψ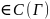 ,(26),где
,(26),где
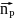 -внешняя
единичная нормаль к поверхности Г в
точке PϵГ.
-внешняя
единичная нормаль к поверхности Г в
точке PϵГ.
Требуется
найти ф-ию u
(D)
,
которая удовлетвор ур-ию (25) в обл D
и граничному усл(26) на граничной
поверхности Г обл D.Задача
Неймана называется 2ой краевой задачей.
Внутр задача Неймана некорктнa,т.е.
не для
непрерывнх граничнх ф-ий ψ
из(26)
решение
задачи,а если
,то
не единственное Внешняя
задача Неймана в R3.Δu=f(x,y,z)в
облD’,(29)
(30),u(M)=>0
при M->
(31).Т5.Если
решение
u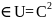 (D’)
(D’)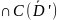 внешней
задачи Неймана (29)-(31),тогда оно единственно
в пространстве U.
внешней
задачи Неймана (29)-(31),тогда оно единственно
в пространстве U.
9.Метод
характеристик. Формула Даламбера для
решения задачи Коши для уравнения
колебаний струны.
Формула
Даламбера. Для
отыскания решения задачи
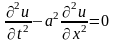 в
в
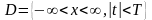 ,
(1)
,
(1)
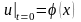 ,
,
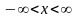 ,
(2)
,
(2)
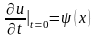 ,
,
(3)
,
,
(3)
применим
метод характеристик. Метод состоит в
приведении исходного уравнения (1) к
каноническому виду и нахождении общего
решения. Для гиперболического уравнения
(1)ур. характ-к имеет вид
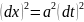 ,
а его характеристиками будут:
,
а его характеристиками будут:
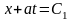 ,
,
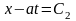 .
.
Производя
замену переменных
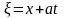 ,
,
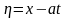 ,приведем
уравнение (1) к каноническому виду
,приведем
уравнение (1) к каноническому виду
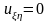 .
Из общего решения имеем
.
Из общего решения имеем
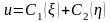 .
Откуда общее решение однородного
уравнения колебаний струны (1)
.
Откуда общее решение однородного
уравнения колебаний струны (1)
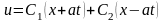 .
(4) Определим неизвестные функции
.
(4) Определим неизвестные функции
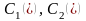 из начальных условий. Подставив (4) в
условие (2), получим соотношение
из начальных условий. Подставив (4) в
условие (2), получим соотношение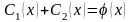 .
(5)Аналогично,
подставляя (4) в условие (3), получаем
.
(5)Аналогично,
подставляя (4) в условие (3), получаем
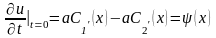 ,
(6)
,
(6)
где
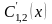 - производные по переменной
- производные по переменной
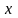 .
.
Интегрируя
равенство (6) по отрезку
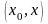 ,
получаем второе соотношение:
,
получаем второе соотношение:
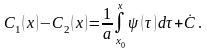 (7)
(7)
Разрешим систему алгебраических уравнений (5), (7), тогда
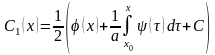 ,
,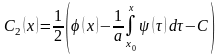 .
.
После подстановки найденных функций в (4) получим формулу Даламбера для решения исходной задачи Коши:
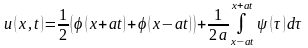 .
(8)
.
(8)
Заметим,
что найденное решение является
классическим, так как
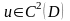 для
для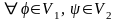 .
.
В случае неоднородного уравнения колебаний струны решение задачи Коши
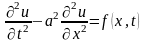 ,
,
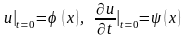
определяется формулой
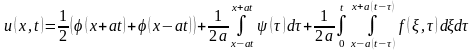 ,
где
,
где
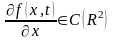 .
.
ЗамечаниеПоставленная з. Коши опред. колебанием бесконечной струны, когда концы струны настолько удалены, что практически не влияют на процесс колебания.
