
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
Задача
Коши для стохастического уравнения.
Требуется определить условную плотность
вероятностей
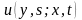 случайного процесса
в момент времени
случайного процесса
в момент времени
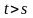 при условии, что случайный процесс
удовлетворяет уравнениям
при условии, что случайный процесс
удовлетворяет уравнениям
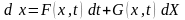 в
в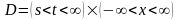 ,
(7.28)
,
(7.28)
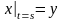 ,
(7.29)
,
(7.29)
где
– заданная постоянная величина,
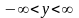 .
.
Задача
Коши для стохастического уравнения в
форме Ито. Требуется
вычислить плотность
процесса
,
который удовлетворяет условиям:
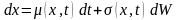 в
,
(7.30)
,(7.31)
в
,
(7.30)
,(7.31)
где
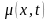 – дрейф;
– дрейф;
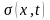 – волатильность
процесса
.
Уравнение (7.30) называется стохастическим
уравнением в форме
Ито.
■
– волатильность
процесса
.
Уравнение (7.30) называется стохастическим
уравнением в форме
Ито.
■
Известно,
что уравнение (7.30) сводится к уравнению
Колмогорова для плотности
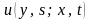 :
:
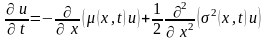 ,
,
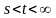 .
(7.32)
.
(7.32)
Сравнивая
уравнения (7.27) и (7.32), заключаем, что
уравнение (7.30) порождает марковский
процесс
,
который определяется функциями
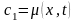 ,
,
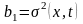 .
.
Для выделения единственного решения уравнения (7.32), учитывая предельное соотношение (5.32) для марковского процесса, к уравнению (7.32) добавим начальное условие и сформулируем определяющую задачу Коши (5.78):
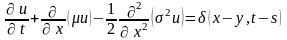 ,
,
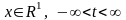 ,
,
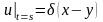 ,
,
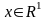 .
(7.33)
.
(7.33)
Как известно, единственное решение задачи (7.33) является фундаментальным решением уравнения (7.32). Таким образом, решение задачи Коши (7.30), (7.31) для стохастического уравнения является переходной функцией плотности вероятностей марковского процесса , которая определяется как решение задачи (7.33) для параболического уравнения.
Марковский процесс подчиняется уравнению (7.27). Поэтому в соответствии со связью между уравнениями (7.30), (7.32) запишем стохастическое уравнение в форме Ито для процесса :
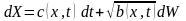 .
(7.34)
.
(7.34)
Подставляя (7.34) в (7.28), преобразуем задачу (7.28), (7.29) к форме Ито:
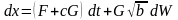 в
,
в
,
.
26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
для
функции
,
которая означает денежные накопления
семьи, было получено стохастическое
дифференциальное уравнение (6.13):
 ,
,
где
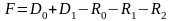 ,
(6.32) величины
,
(6.32) величины
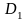 ,
,
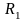 ,
,
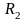 определяются формулами (6.4), (6.7), (6.8).
определяются формулами (6.4), (6.7), (6.8).
Пусть
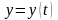 – материальные накопления семьи в
момент времени
.
Отрицательное значение величины
означает материальный долг семьи.
Естественно, что в большей степени
скорость
– материальные накопления семьи в
момент времени
.
Отрицательное значение величины
означает материальный долг семьи.
Естественно, что в большей степени
скорость
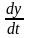 изменения материальных накоплений
семьи опр-ся детерминированными денежными
расходами . Изменение детерминированных
материальных накоплений семьи в общем
случае выразим уравнением
изменения материальных накоплений
семьи опр-ся детерминированными денежными
расходами . Изменение детерминированных
материальных накоплений семьи в общем
случае выразим уравнением
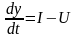 ,
(6.33) где
,
(6.33) где
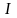 – приобретенное имущество в руб. за
месяц
– приобретенное имущество в руб. за
месяц
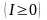 ;
;
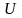 – утраченное имущество в рублях за
месяц
– утраченное имущество в рублях за
месяц
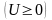 .
.
Уравнение
(6.33) запишем в дифф-лах и преобразуем в
стохаст-ое уравнение, добавив стохаст-й
дифф-л. Получим
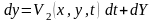 ,
(6.34) где
,
(6.34) где
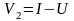 ;
;
 – стохастический дифференциал;
– стохастический дифференциал;
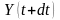 – случайные материальные накопления
к моменту времени
– случайные материальные накопления
к моменту времени
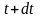 ;
;
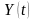 –случайные
материальные накопления к моменту
времени
В результате уравнение (6.31) принимает
вид
–случайные
материальные накопления к моменту
времени
В результате уравнение (6.31) принимает
вид
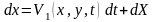 ,
(6.36) , где
,
(6.36) , где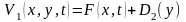 .
.
1.
Вычислим
.
Имущество приобретается в основном за
счет денежных расходов
и
,
определяемых формулами (6.7), (6.8). Поэтому
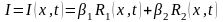 .
(6.37) Безразмерные коэффициенты
.
(6.37) Безразмерные коэффициенты
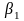 и
и
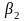
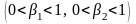 задают части от израсходованных денег,
кото-рые определяют реальную стоимость
товара. Оставшаяся часть денег расходуется
на торговую наценку, доставку товара и
так далее, то есть не определяет
материальные накопления семьи. 2.
Вычислим
.
Имущество в основном утрачивается за
счет амортизации, то есть за счет
изнашивания, поэтому полагаем
задают части от израсходованных денег,
кото-рые определяют реальную стоимость
товара. Оставшаяся часть денег расходуется
на торговую наценку, доставку товара и
так далее, то есть не определяет
материальные накопления семьи. 2.
Вычислим
.
Имущество в основном утрачивается за
счет амортизации, то есть за счет
изнашивания, поэтому полагаем
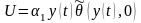 ,
где
,
где
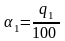 ,
,
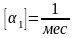 ;
;
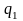 – процент изнашивания в месяц. В рез-те
– процент изнашивания в месяц. В рез-те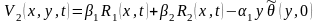 .
.
Т.о,
получена система стохастических диф-ных
ур-й (6.34),(6.36):
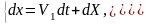 (6.38)
(6.38)
Запишем
систему (6.38) в векторном виде
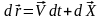 ,
(6.39) где
,
(6.39) где
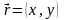 ,
,
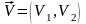 ;
– двухмерный стохастический процесс.
;
– двухмерный стохастический процесс.
Двухмерная случайная величина описывает случайное выпадение точки (семьи) на плоскость N , то есть случайные денежные и материальные накопления семьи в момент времени .
