
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
Введем
в рассмотрение оператор Лапласа Δ по
формуле: Δu=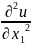 +
+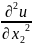 +...+
+...+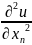 .
Уравнением
Лапласа будем
называть ур-ние: Δu=0(1),
заданное в некоторой обл Ω≤Rn.
Г=
.
Уравнением
Лапласа будем
называть ур-ние: Δu=0(1),
заданное в некоторой обл Ω≤Rn.
Г= Ω-граница
обл Ω. Ф-цию u
будем называть гармонической
на
обл Ω,если она принадлежит классу С2(Ω)
и удовлетворяет ур-нию (1) на обл Ω. Если
Ω неограничена(т.е. включает в себя
бесконечно удаленную точку), то добавляется
требование u(M)
Ω-граница
обл Ω. Ф-цию u
будем называть гармонической
на
обл Ω,если она принадлежит классу С2(Ω)
и удовлетворяет ур-нию (1) на обл Ω. Если
Ω неограничена(т.е. включает в себя
бесконечно удаленную точку), то добавляется
требование u(M)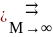 0.
0.
Рассмотрим
формулы Грина, связывающие значения
ф-ции u
на границе Ω со значениями ф-ции u
на облΩ. Рассмотрим 3ех мерный случай.Из
теории векторных полей, имеем Δu=div(grad
u).
div(a
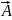 )=a
div
+(grad
a,
)=a
div
+(grad
a,
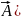 (2).
В (2) будем считать a=v(x,y,z),
=grad
u(x,y,z).
Тогда (2) примет вид div(v∙grad
u)=v∙Δu+(grad
v,grad
u).
Проинтегрируем это равенство по
облΩ:
(2).
В (2) будем считать a=v(x,y,z),
=grad
u(x,y,z).
Тогда (2) примет вид div(v∙grad
u)=v∙Δu+(grad
v,grad
u).
Проинтегрируем это равенство по
облΩ: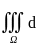 iv(v∙grad
u)dV=
iv(v∙grad
u)dV=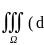 V∙Δu+(grad
v,grad
u))dV.
Применим формулу Остроградского, где
n-внешняя
единичная нормальная поверхность
Г,получим:
V∙Δu+(grad
v,grad
u))dV.
Применим формулу Остроградского, где
n-внешняя
единичная нормальная поверхность
Г,получим:
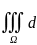 iv
iv
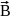 dV=
dV=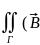 ,
,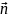 )ds.
По свойству скалярн произведения:
)ds.
По свойству скалярн произведения: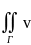 (grad
u,
(grad
u,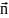 )ds=
)ds= vΔu+(grad
v,grad
u))
dV.
vΔu+(grad
v,grad
u))
dV.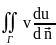 ds=
vΔu+(grad
v,grad u))dV(3)-1-ая
формула
Грина
ds=
vΔu+(grad
v,grad u))dV(3)-1-ая
формула
Грина
Поменяем
местами в (3)ф-ии u
и v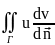 ds=
uΔv+(grad
u,grad
v))dV(*).
Вычтем (3) из (*):
ds=
uΔv+(grad
u,grad
v))dV(*).
Вычтем (3) из (*):
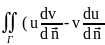 )ds=
uΔv-vΔu)dV(4)
-2-ая
формула Грина.
)ds=
uΔv-vΔu)dV(4)
-2-ая
формула Грина.
Положим,
что в (3) u
и v
совпадают: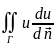 ds=
ds= uΔu+|grad
u|2)dV(5)-3-ья
формула Грина
uΔu+|grad
u|2)dV(5)-3-ья
формула Грина
Восстановим
значения гармонической ф-ции u
на обл Ω через ее значения на границе
Г. Для этого убедимся,что ф-ция v(M)=1/r,
r=|MM0|(6),удовлетворяет
3ехмерному ур-нию
Лапласа(1),(M0(x0,y0,z0)-фиксированная
точка)за исключением т.М0.
Решением (6) 3ехмерн ур-ния Лапласа
называют фундаментальным
решением.Попытаемся
восстановить значения ф-ции u
в некоторой т.М0
обл
Ω через ее значения на границе Г. Чтобы
положить во 2-ой ф-ле Грина v(M)=1/4πr
(7)-решение
3мерного ур-я Лапласа, мы исключим точку
М0,описав
вокруг нее сферу Гε
радиуса
ε и рассмотрим обл Ωε,заключенную
между поверхностями Г и Гε.
ОчевидноΩε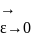 Ω.
Поскольку(7)-гармоническое ур-ние на
всей обл Ωε,то
можем применить к этой обл 2-ую формулу
Грина(4),при этом поверхностный интеграл
должен браться по всей поверхности,ограниченной
обл Ω
Ω.
Поскольку(7)-гармоническое ур-ние на
всей обл Ωε,то
можем применить к этой обл 2-ую формулу
Грина(4),при этом поверхностный интеграл
должен браться по всей поверхности,ограниченной
обл Ω
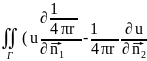
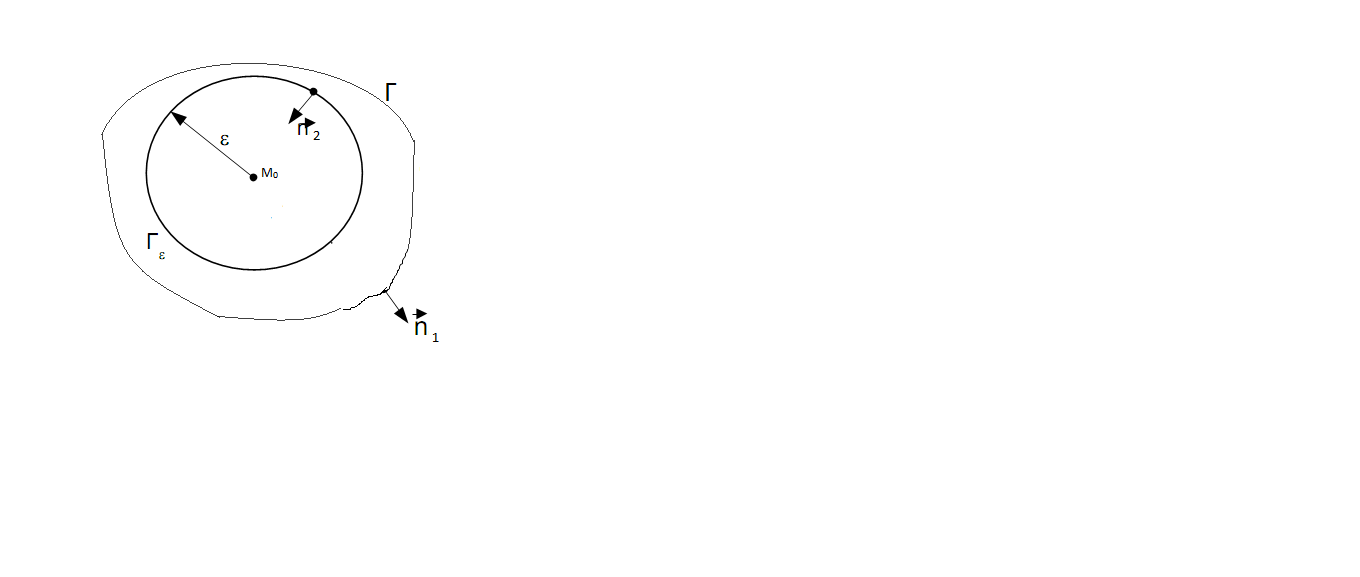 )ds+
)ds+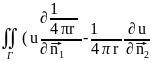 )ds=-
)ds=-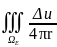 dV.
dV.
Вычислим
поверхностный интеграл по сфере Гε
для
этого вычислим
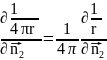 =
=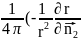 )=-
)=-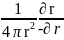 =
=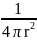 ,тогда
,тогда
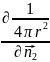 |Г2=
|Г2=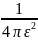
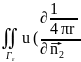 )ds=
)ds=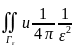 ds=
ds=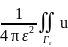 ds=
ds=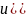 s(P*-некотрая
точка просранства Гε)=u(P*).
s(P*-некотрая
точка просранства Гε)=u(P*).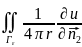 ds=
ds=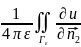 ds=
ds=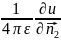 |p*
|p*
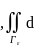 s=
s=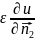 |
|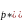 ,
,
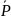 *
*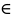 Гε.Тогда
Гε.Тогда
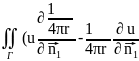 )ds+u(P*)-ε
)ds+u(P*)-ε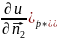 =-
=-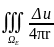 dV,переходим
к
пределу
при
ε→0
dV,переходим
к
пределу
при
ε→0
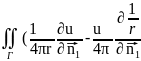 )ds
+u(M0)=-
)ds
+u(M0)=-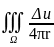 dV,
u(M0)=
)ds-
dV,
u(M0)=
)ds-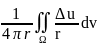 получили
формулу,справедливую
для
любой,достаточно
гладкой
ф-ции
u.
получили
формулу,справедливую
для
любой,достаточно
гладкой
ф-ции
u.
Если
ф-ция u
является гармонической u(M0)=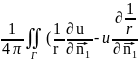 )ds
(8)-интегральная
формула Грина позволяет
восстановить значения ф-ции u
в любой т.М0
через ее значения на границе Г
)ds
(8)-интегральная
формула Грина позволяет
восстановить значения ф-ции u
в любой т.М0
через ее значения на границе Г
Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
Св-во1.Пусть
u(x,y,z)-гармоническая
ф-ия
в области D,тогда ф-ция
u любое число раз непрерывно дифференцируема
по координатам x,y,z
в
области D,то есть u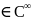 (D).
(D).
Св-о
2.(Теорема
о нормальной производной).Пусть
любая
ф-ция
u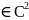 (D)
(D)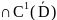 и
является гармонической в области D,
и
является гармонической в области D,
Тогда
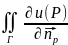 dSp=0,Г=∂D.
dSp=0,Г=∂D.
Св-во
3.
Т-ма о среднем.
Пусть u-гармоническая
ф-ция в обл D,
тогда для
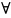 M
M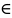 D
и
сферы
D
и
сферы
 ,
,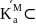 D,
имеет
место формула u(M)=
D,
имеет
место формула u(M)=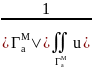 (P)dSP
(4.13),где
|
(P)dSP
(4.13),где
|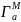 |=4
|=4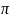 a2-площадь
сферы.
a2-площадь
сферы.
В
плоском случае имеем формулу u(M)=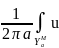 (P)dlP*
(P)dlP*
Рассмотрим связную ограниченную область D R3с границей Г=∂D. Будем считать для определенности, что Г С.В обл задана ф-ия u=u(x,y,z)=u(M).
Св-во4.Принцип
максимума и минимума.
Пусть u
(D)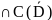 и
удовлетворяет в обл D
ур-нию Лапласа Δu=0.Тогда
ф-ция u
достигает своего максимального и
минимального значений на границе Г,
т.е.
и
удовлетворяет в обл D
ур-нию Лапласа Δu=0.Тогда
ф-ция u
достигает своего максимального и
минимального значений на границе Г,
т.е.
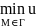 (M)
≤u(
(M)
≤u(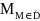 )≤
)≤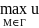 (M).
(M).
Следствие
1.Пусть ф-ции u,v
(D)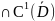 и являются гармоническими в D. Если
u(P)≥v(P) для
PϵГ,
то u(М)≥v(M) для
M
и являются гармоническими в D. Если
u(P)≥v(P) для
PϵГ,
то u(М)≥v(M) для
M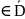 .
.
Следствие
2. Пусть функции u1,u2,u3
(D)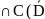 )
и
явл-ся гармоническими в D.
Если u1(P)≤u2(P)≤u3(P)
для
P
Г,то
u1(М)≤u2(М)≤u3(М)
для
M
)
и
явл-ся гармоническими в D.
Если u1(P)≤u2(P)≤u3(P)
для
P
Г,то
u1(М)≤u2(М)≤u3(М)
для
M
Следствие
3. Пусть ф-ии u,v
(D)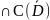 и являются гармоническими в D.
Если |u(P)|≤v(P)
для
PϵГ,
то |u(М)|≤v(M)
для
M
.
и являются гармоническими в D.
Если |u(P)|≤v(P)
для
PϵГ,
то |u(М)|≤v(M)
для
M
.
Следс.4. Пусть ф-ия u (D) и является гармонической в D. Если |u(P)|≤ε, ε=const, для PϵГ, то |u(М)|≤ε для M .
