
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
Примером
сингулярной обобщенной функции может
служить -функция Дирака. Зафиксируем
нек.точку
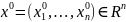 и построим функционал
и построим функционал
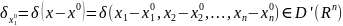 ,
кот.действ.на ф-ию
,
кот.действ.на ф-ию
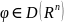 след.образом
след.образом
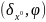 =
=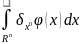 =
=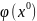 .
.
В
частном случае, если точка
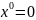 – нач.координата, то
– нач.координата, то
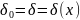 .
.
Из св-в интегр. Вытекает, что функционал -лин.и непрерывн., а значит он явл.обобщенной функцией. Такая фун. И наз-ся -функция Дирака.
Рассмотрим
открытое мн-во
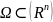 .
Будем говорить, что обобщенная фун-я
f=0 на
,
если
.
Будем говорить, что обобщенная фун-я
f=0 на
,
если
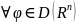 выполнены условия
выполнены условия
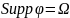 ,
то (f,
)=0.
,
то (f,
)=0.
Обозначим
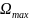 -наибольшее
открытое множество, на котором обобщенная
функция f=0, тогда насителем обобщенной
ф-ии f будем называть замкнутое множество
-наибольшее
открытое множество, на котором обобщенная
функция f=0, тогда насителем обобщенной
ф-ии f будем называть замкнутое множество
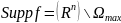 .
Из зад.
–функции Дирака вытекает
.
Из зад.
–функции Дирака вытекает
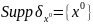 .
Носителем будет
.
Вне этой точки фун-я Дирака зануляется.
.
Носителем будет
.
Вне этой точки фун-я Дирака зануляется.
Рассмотрим
обобщенную фун-ю вида
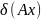 ,
где А- невырожденная матрица. Действие
функционала
на функцию
осуществляется след.образом:
,
где А- невырожденная матрица. Действие
функционала
на функцию
осуществляется след.образом:
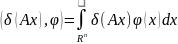 .
(1)
.
(1)
В интеграле (1) выполнена замена переменной y=Ax, тогда
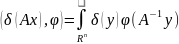 |I|dy=|I|.
Получим соотношение
|I|dy=|I|.
Получим соотношение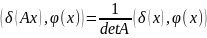 .
Определим произв.
.
Определим произв.
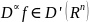 .
Обобщенная фу-я
.
Обобщенная фу-я
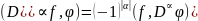 .
(2)
.
(2)
Т.к.
фун-я
из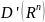 ,
то прав.часть (2) определена, а тем самым
и определен функционал
,
то прав.часть (2) определена, а тем самым
и определен функционал
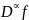 ,
кот. Явл. Непрерывн., т.е. является
обобщенной ф-ей. Формула (2) позволяет
найти произведение от любой огранич.функции.
,
кот. Явл. Непрерывн., т.е. является
обобщенной ф-ей. Формула (2) позволяет
найти произведение от любой огранич.функции.
Опр.
Будем говорить, что функция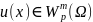 ,
где
,
где
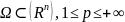 ,
если сама функция
,
если сама функция
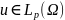 и всевозможные
и всевозможные
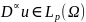 ,
,
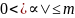 ,
,
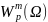 - пространство Соболева.
- пространство Соболева.
Рассмотрим
ДУ с ч.п.
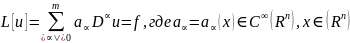 .(1)
.(1)
Опр.
Обобщенная функция u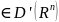 наз.обобщенным решением ур.(1), если
выполн.тождества
наз.обобщенным решением ур.(1), если
выполн.тождества
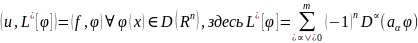 -сопряженный
дифференциальный оператор к L.
-сопряженный
дифференциальный оператор к L.
15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
Рассмотрим ДУ с ч.п. .(1)
Опр. Обобщенная функция u наз.обобщенным решением ур.(1), если выполн.тождества -сопряженный дифференциальный оператор к L.
Пусть
в правой части ур.(1) стоит
–функция:
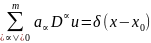 (2). Любое обобщенное решение
(2). Любое обобщенное решение
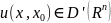 ур.(2) называется фундаментальной функцией
оператора L.
Естественно, что фундамент.фун-я опер.L
определ.неоднозначно. Для однозначности
накладывают дополнительные условия
нормировки. Это выделяет единств.фундамент.фун-ю
ур.(2) называется фундаментальной функцией
оператора L.
Естественно, что фундамент.фун-я опер.L
определ.неоднозначно. Для однозначности
накладывают дополнительные условия
нормировки. Это выделяет единств.фундамент.фун-ю
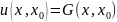 ,
кот.наз-ся фундамент.реш.ур.(2).
,
кот.наз-ся фундамент.реш.ур.(2).
Рассм.ур-е
Колмогорова неоднородное с
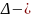 функцией,
т.е.ур.вида
функцией,
т.е.ур.вида
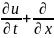 (c(t,x)u)-
(c(t,x)u)-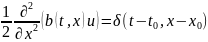
(3),кот.я явл-ся уравн.вида (2).
Если
параметры с и b
– постоянные, то ур (3) приведем к виду:
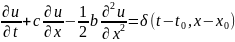 (4) выполняя параллельный перенос (4)
приведем к виду:
(4) выполняя параллельный перенос (4)
приведем к виду:
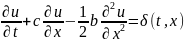 (5). Найдем фундаментальное решение ур
(5), потребовав дополнительно, чтобы
решение
(5). Найдем фундаментальное решение ур
(5), потребовав дополнительно, чтобы
решение
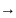 0,
когда
0,
когда
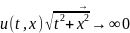 (6). В уравнении (5) выполним замену
(6). В уравнении (5) выполним замену
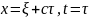 .
Тогда ур.(5) примет вид:
.
Тогда ур.(5) примет вид:
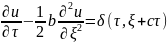 .
По св-ву
функции,
ур.приведем к виду:
.
По св-ву
функции,
ур.приведем к виду:
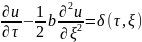 .(7)
Выполним еще одну замену:
.(7)
Выполним еще одну замену: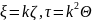 ,
тогда(применяя сво-во дельта-функции):
,
тогда(применяя сво-во дельта-функции):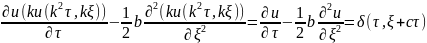 .(8).
Формально, ур(7) и (8) одинаковы. В силу
усл. (6) их фундамент.реш.единственны, а
зн.совпадают. Значит
.(8).
Формально, ур(7) и (8) одинаковы. В силу
усл. (6) их фундамент.реш.единственны, а
зн.совпадают. Значит
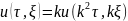 .
Это рав-во справедливо
.
Это рав-во справедливо
 Выберем
Выберем
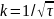 и введем нов.переменную
и введем нов.переменную
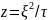 .(9)
Тогда
.(9)
Тогда
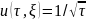 w(z),
w(z)-
фун-я
w(z),
w(z)-
фун-я
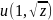 .
.
Подставим
(9) в (7). После приведения подобных получим
ОДУ 2 порядка( и т.к. при положительных
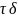 -функция
=0)получим:
-функция
=0)получим:
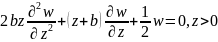 .
Это ДУ Эйлера, откуда с учетом требования
(6), чтобы занулить
.
Это ДУ Эйлера, откуда с учетом требования
(6), чтобы занулить
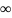 ,
выбираем решение
,
выбираем решение
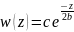 .
Чтобы данная функция или реш. было
нормиров.
.
Чтобы данная функция или реш. было
нормиров.
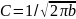 ,
тогда
,
тогда
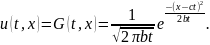 (10).
Функция (10) явл.фундаментальным решением
ур.Колмогорова(5) при t>0.
При t<0
фунд.реш. определено нулем. Произведя
обратный сдвиг координат (t,x)
на величины
(10).
Функция (10) явл.фундаментальным решением
ур.Колмогорова(5) при t>0.
При t<0
фунд.реш. определено нулем. Произведя
обратный сдвиг координат (t,x)
на величины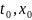 соотв. Получим фунд.решение ур.(4).
соотв. Получим фунд.решение ур.(4).
