
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
Пусть
конкретная семья к моменту времени t
накопила общую сумму денег x(t),
t
измеряем в месяцах, x
– в рублях. В рассмотр. введём про-во R
изображ. На оси Ox
каждую семью будем изображать на R
точкой, координата которой соотв.
денежным накоплениям семьи. Про-во R
с такой физической интерпретацией будем
называть пр-вом денежных накоплений и
обозначать
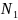 .
Отриц. Значения в
интерпретируем
как как долг. Помимо гарантированных
накоплений, семья может иметь случайные
накопления, которые будем рассматр. как
одномерную случ. величину X.
Представим, что некоторый прибор
выбрасывает точку X
на ось Ox
случ. образом, но по некоторому внутреннему
правилу. Поэтому в нек. местах точка Х
встречается чаще чем в других.
.
Отриц. Значения в
интерпретируем
как как долг. Помимо гарантированных
накоплений, семья может иметь случайные
накопления, которые будем рассматр. как
одномерную случ. величину X.
Представим, что некоторый прибор
выбрасывает точку X
на ось Ox
случ. образом, но по некоторому внутреннему
правилу. Поэтому в нек. местах точка Х
встречается чаще чем в других.
x
X
Координата х выбрасываемой т. о. точки назыв. случ. величиной, обозн. X. Однако сама координата не задаёт свою величину. Для задания случайной величины введем функцию плотности распределения вероятностей со следующими свойствами:
-
определена при
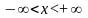 ,
,
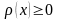 ,
,
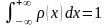 (1)
(1)
Таким
образом, случайная величина
определена,
если задана плотность вероятностей
.
Физически плотность вероятности имеет
след. смысл:
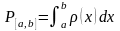 означает
вероятность того, что случайная величина
x
попадает на отрезок
означает
вероятность того, что случайная величина
x
попадает на отрезок
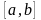 , то есть денежные накопления семьи
находятся в пределах от a
до b.
В реальности денежные накопления семьи
непостоянны. Поэтому плотность
распределения случайной величины
, то есть денежные накопления семьи
находятся в пределах от a
до b.
В реальности денежные накопления семьи
непостоянны. Поэтому плотность
распределения случайной величины
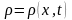 .
В этом случае имеем стохастический
процесс x(t),
что значит, что в данный момент времени
t
случайная величина x(t)
имеет свою плотность. Введем еще два
параметра y
и s
:
.
В этом случае имеем стохастический
процесс x(t),
что значит, что в данный момент времени
t
случайная величина x(t)
имеет свою плотность. Введем еще два
параметра y
и s
:
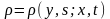 ,
,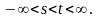
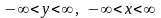 (2)
(2)
где y означает значение случ. величины x(s), которое она приняла в предыдущий момент времени s; x означает значение случайной величины x(t), которое она примет в последующий момент времени t.
Опр. Функция (2) называется переходной функцией плотности вероятностей или условной плотностью вероятностей стохастического процесса X(t).
Опр.
Стохастический процесс называется
марковским,
если
для любых
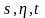
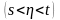 выполнено тождество
Маркова- Колмогорова-Чепмена:
выполнено тождество
Маркова- Колмогорова-Чепмена:
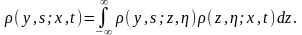 (3)
(3)
В
дальнейшем будем рассматривать
стохастические процессы, для которых
выполнены следующие условия при
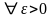 и
и
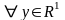 :
:
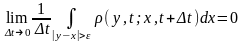
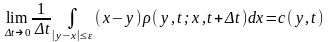 (4)
(4)
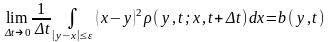
Условия (4) называются условиями сильной непрерывности марковского процесса, а процесс называется диффузионным.
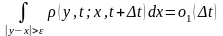
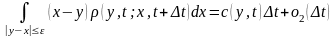
19.Постановка смешанных задач для уравнения теплопроводности в стержне.
На
плоскости
с координатами
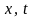 выделим область
.В
области
рассмотрим уравнение теплопроводности
выделим область
.В
области
рассмотрим уравнение теплопроводности
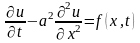 ,
(1) где
,
(1) где
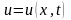 - искомая функция в области
.
Уравнение (1) называется также одномерным
уравнением теплопроводности.
- искомая функция в области
.
Уравнение (1) называется также одномерным
уравнением теплопроводности.
Для
параболического уравнения (1) поставим
смешанные задачи первого, второго и
третьего рода, наложив на функцию
одно начальное условие на нижнем
основании
и граничные условия на боковых сторонах
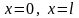 полуполосы
.
полуполосы
.
Первая смешанная задача.
в области , (2)
, , (3)
, , . (4)
При
заданных функциях
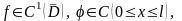
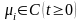 требуется найти функцию
требуется найти функцию
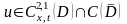 ,
которая удовлетворяет уравнению (2) в
области
,
начальному условию (3) и граничным
усл первого рода
(4). Функции
,
которая удовлетворяет уравнению (2) в
области
,
начальному условию (3) и граничным
усл первого рода
(4). Функции
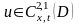 ,
если
,
если
 .
.
Условия
согласования:
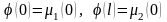 .
.
Задача
(2)-(4) описывает процесс распространения
тепла в тонком стержне длины
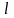 ,
расположенном вдоль отрезка
.Функция
,
расположенном вдоль отрезка
.Функция
 задает температуру стержня в сечении
в момент времени
.
Граничные условия (4) означают, что в
торцах стержня
поддерживаются заданные температуры
задает температуру стержня в сечении
в момент времени
.
Граничные условия (4) означают, что в
торцах стержня
поддерживаются заданные температуры
 ,
,
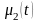 .
Функция
в начальном условии (3) задает температуру
стержня в каждом сечении
в начальный момент времени
.
.
Функция
в начальном условии (3) задает температуру
стержня в каждом сечении
в начальный момент времени
.
Вторая смешанная задача.
в области , (5)
, , (6)
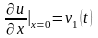 ,
,
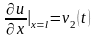 ,
.
(7)
,
.
(7)
При
заданных функциях
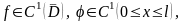
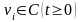 требуется найти функцию
требуется найти функцию
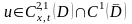 ,
которая удовлетворяет уравнению (5) в
области
,
начальному условию (6) и граничным
усл второго рода
(7).
,
которая удовлетворяет уравнению (5) в
области
,
начальному условию (6) и граничным
усл второго рода
(7).
Условия
согласования:
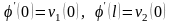 .
.
Граничные
условия (7) означают, что в торцах стержня
 заданы тепловые потоки.
заданы тепловые потоки.
Третья смешанная задача.
в области , (8)
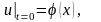 ,
(9)
,
(9)
, . (10)
При
заданных функциях
 ,
,
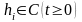 требуется найти функцию
,
которая удовлетворяет уравнению (8) в
области
,
начальному условию (9) и граничным
усл третьего рода
(10).
требуется найти функцию
,
которая удовлетворяет уравнению (8) в
области
,
начальному условию (9) и граничным
усл третьего рода
(10).
Условия
согласования:
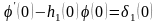 ,
,
 .
.
Граничные
условия (10) моделируют теплообмен стержня
через торцы
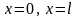 с окружающей средой.
с окружающей средой.
Заметим, что для существования классических решений сформулированных задач необходимо на начальные и граничные функции и на правую часть уравнения теплопроводности накладывать некоторые дополнительные условия.
