7. Поле, образованное двумя разноименными заряженными плоскостями (бесконечно большими)

Поле двух параллельных бесконечно больших плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью можно рассматривать как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями (рис.2.13) складываемые поля имеют одинаковое направление, так что результирующая напряженность равна

(4)

В не объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю E=0. Таким образом, поле сосредоточено между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению. Поле, обладающее такими свойствами, называется однородным. Линии напряженности однородного поля представляют собой совокупность параллельных равноотстоящих прямых.

Полученный результат приблизительно справедлив и в случае плоскостей конечных размеров, если расстояние между плоскостями значительно меньше их линейных размеров (плоский конденсатор). В этом случае заметные отклонения поля от однородности напряженности наблюдаются только вблизи краев пластин (рис. 2.14).

Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ .

Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей. Тогда внутри плоскостей

Вне плоскостей напряженность поля .

Распределение напряженности электростатического поля между пластинами конденсатора показано на рисунке .

Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):

, т.е. .

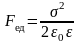Механические силы, действующие между заряженными телами, называют пондермоторными.

Тогда сила притяжения между пластинами конденсатора:

где S – площадь обкладок конденсатора. Т.к. , то

.

Это формула для расчета пондермоторной силы.

8.Теорема Гаусса в дифференциальной форме.

Записанная ранее форма теоремы называется интегральной. Дифференциальная форма теоремы Гаусса устанавливает связь между объемной плотностью заряда и изменениями напряженности Е в окрестности данной точки пространства.

Заряд в V

Теорема Гаусса:

Устремим V к нулю ( )

Теорема Гаусса в дифференциальной форме:

В дифференциальной форме теорема Гаусса является локальной теоремой: дивергенция поля Е в данной точке зависит только от плотности электрического заряда ρ в той же точке.

9. Работа сил электростатического поля. Потенциал электрического поля.

Сила, действующая на точечный заряд, находящийся в поле другого неподвижного точечного заряда, является центральной. Центральное поле сил – потенциально. Вычислим работу, совершаемую силами поля неподвижного точечного заряда q над перемещающимся в этом поле зарядом q'.

П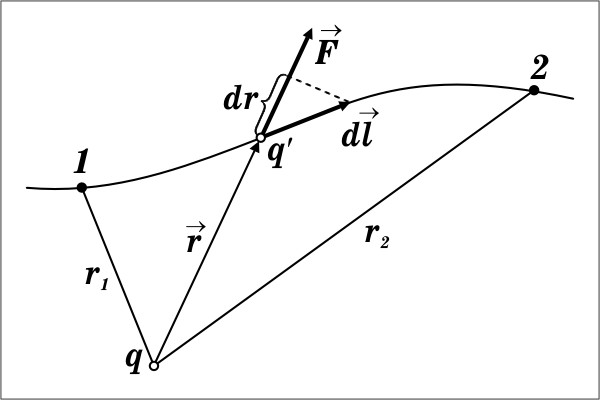 уть dl:

8

Работа не зависит от пути, по которому перемещался в электрическом поле заряд q', а зависит только от начального и конечного положений этого заряда. Следовательно, силы, действующие на заряд q' в поле неподвижного заряда q, являются потенциальными. Этот вывод легко распространяется па поле любой системы неподвижных зарядов.

Работа потенциальных сил по замкнутому контуру равна нулю: Циркуляция вектора напряженности по любому замкнутому контуру равна нулю – теорема о циркуляции вектора E. Это характерно только для электростатического поля.

Потенциал.

Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля. Работа может быть представлена как разность значений потенциальной энергии, которыми обладал заряд q' в точках 1 и 2 поля заряда q:

Потенциальная энергия заряда q'

Значение сonst выбирается т.о., чтобы при удалении от заряда на бесконечность потенциальная энергия обращалась в нуль. Если использовать зарядом q' в качестве пробного то потенциальная энергия, этого заряда, зависит от величины q', и от величин q и r, определяющих поле. Эта энергия может быть использована для описания поля, как и сила, действующая на пробный заряд. Величина будет одной и той же для всех пробных зарядов.

φ называется потенциалом поля в данной точке и используется для описания электрических полей. Потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.

- потенциал поля точечного заряда. Пусть поле создано системой точечных зарядов q1, q2… Работа, совершаемая силами этого поля над зарядом q', будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности

Потенциальная энергии и потенциал заряда q' в поле системы зарядов:

Потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.

Потенциальная энергия точечного заряда:

Работа, совершаемая над точечным зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках.