11. Формула полной вероятности.

Если событие А может произойти при появление одной из гипотез, то его вероятность равна сумме произведений вероятностей каждой гипотезы и соответствующих условных вероятностей события А:

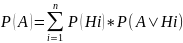
12.Формула Байеса.

Пусть событие А происходит одновременно с одним из n-несовместных событий Н₁, Н₂…Н_n и вероятности Р(Н_i) 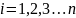известны до опыта. Производится опыт в результате которого зарегистрировано появление события А при чём известно, что это событие имело определённые условные вероятности Р(А/Н_i) i=1,2…n и требуется найти вероятности события Н_i, если известно что событие А произошло. .

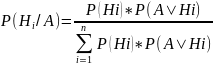13. Повторные независимые испытания.

14. Формула Бернулли. Наивероятнейшее число наступления события.

Пусть в результате испытания возможно 2 исхода: 1)появится событие А;

2)появится противоположное событие 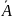. Проводим n испытаний, события независимы и Р(А)=р, Р( =q=1-р

тогда .

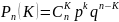Где n-кол-во испытаний

K-кол-во удачных испытании

C^k_{n=n!/K!(n-K)! (без упорядочивания без возвращения!/)}

ПР: найти вероятность того, что стрелок попадёт 3 раза в мишень из 5 выстрелов, если вероятность попадания в мишень для стрелка 0,8

n=5 K=3 P=0,8 g=1-р=0,2

Наивероятнейшее число наступления события а в испытанмях Бернули

np-g<m найвероятнейш.<np+p

Пример:

При автоматической наводке орудия вероятность попадания по быстро движущее цели=0,9. Найти найвероятнейшее число попаданий при 50 выстрелов.

n 50 p=0,9 g=0,1

50*0,9*0,1<m<50*0,9*0,9* 44,9<m<45,9 m найв=45

15.Локальная формула Муавра-Лапласа.

Если вероятность (р)появления события А в каждом испытании постоянно и отлично от 0 до 1, то вероятность Р_n(К) того, что событие А в n испытаниях появятся ровно К раз, приближенно равно:

Р_n(К)= .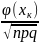

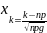
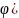
Прим: Найти вероятность того, что событие А наступят ровно 80 раз из 400 испытаний.

Вероятность появления события А=0,2

n=400 K=80 p=02 g=08

16.Интергральная формула Муавра-Лапласа.

Если вероятность наступления события А в каждом испытании постоянно и отлично от 0 и 1, то Р_n(X_K1, X_K2) или Р_n(К_1, К₂), то событие А появится в n испытаниях от К₁ до К₂ раз приближенно равно

Р_n(К_1, К₂)=Ф(X_K2)-Ф(X_K1).

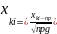
17. Формула Пуассона

Если вероятность наступления события А в каждом испытании постоянно но мала, а число независимых испытаний достаточно велико 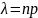также неброльшое (не больше 10)то вероятность того, что в этих испытаниях событие А наступит К-раз ͌ /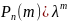

ПРИМЕР:

Пусть вероятность изготовления нестандартных деталей =0,004. Найти вероятность того что среди 1000 деталей окажетсяh 5 нестандартных.

P=0,004 m=5 n=10000

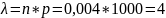
е=2,7

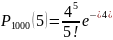=0?1563