
- •Предмет теории вероятностей. Возникновение теории вероятностей.
- •Элементарные сведения из теории множеств.
- •Пространство элементарных событий. Случайные, достоверные, невозможные и несовместные события.
- •4. Действия над событиями (объединение, пересечение, разность).
- •2)Пересечение(произведение)-
- •5. Классическое определение вероятности.
- •6. Геометрическое определение вероятности.
- •7.Схема выбора без возвращения (сочетания, размещения).
- •8. Схема выбора с возвращением (перестановки, сочетания и размещения с повторением).
- •9.Теоремы сложения вероятности.
- •10.Теорема умножения вероятности.
- •11. Формула полной вероятности.
- •12.Формула Байеса.
- •13. Повторные независимые испытания.
- •Формула Бернулли. Наивероятнейшее число наступления события.
- •Наивероятнейшее число наступления события а в испытанмях Бернули
- •15.Локальная формула Муавра-Лапласа.
- •16.Интергральная формула Муавра-Лапласа.
- •17. Формула Пуассона
- •18.Случайная величина.
- •19 , 20.Дискретно распределённая случайная величина.
- •21.23 Непрерывно распределённая случайная величина.
- •22. Плотность распределения непрерывной случайной величины
- •24.Биномиальный закон распределения св.
- •25 . Распределение Пуассона св.
- •26.Нормальный закон распределение св (распределение Гаусса).
- •27. Геометрическое распределение случайной величины
- •28. 29Неравенство Чебышева.
- •30.Теорема Бернулли.
- •31.Генеральная и выборочная совокупность.
- •32 .Вариационный ряд
- •34.Эмперическая функция распределения.
- •36.Точечное оценивание параметров распределения.
- •34.Интервальное оценивание параметров распределения.
- •Критическая область, мощность критерия.
- •37. Схема проверки стат-ой гипотезы.
- •42. Основные понятия корреляционного и регрессионного анализа.
- •43)Линейная корреляционная зависимость и прямые регрессии
- •44)Коэффициент линейной корреляции и его свойства
8. Схема выбора с возвращением (перестановки, сочетания и размещения с повторением).
Перестановкой из n-элементов наз.- размещение из элементов по n-элементов.
Рn=n!
ПР: Сколькими способами можно рассадить 5 человек по 5 местам.
P5=5!=12345=120
Если n-это v-выборки, n1=количество элементов 1-го вида, n2-количество элементов 2-го вида, nn-кол-во элем.n-го вида., то перестановкой
Рn(n1,n2,….nn)=n!/n1!n2!....nn!
ПР: Сколько различных четырех знатных номеров для машин можно составить из цифр:2,1,0,9,2.
N=5
n1=2; n2=1; n3=1; n4= 1; n5=1. Р5=5!/2!*1!*1!*1!=5!/2!.
Выборка с возвращения и без упорядочивания (Схема выбора проводящая к сочетанию, но с повторением)Суть выборки из n-элементов выбирает m-элемент выбирают с возвращения и без упорядочивания следования элементов.
Число сочетаний из n-элементов опред. След. Фор.
Схема выбора с возвращением (перестановки, сочетания и размещения с повторением).
Из 10 цифр от 1до 10 выбирают 4 числа с возвращением.
n=10 m=6
С410 =(10+4-1)!/4!*(10-1)! =13!/4!*9!=5*11*12*13/1234=5*11*13=715
10!=1*2*3*4*5*6*7*8*9*10
Выборка с возвращения и c упорядочивания .
Суть выборки из n-элементов выбирает m-элемент выбирают с возвращения , но с упорядочивания следования элементов.
Число размещения из n-элементов по m-элементам опред. След. Фор.
ПР: Сколько способами можно рассадить 7 человек по 9 вагонам.
А79=97
9.Теоремы сложения вероятности.
Теорема: Вероятность появления хотя бы одного из совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления (если события А и В совместны): Р(А+В)=Р(А)+Р(В)-Р(АВ).
Пусть А1, А2…Аn несовместные, то вероятность их суммы: Р(А1+А2+…+Аn)=Р(А1)+Р(А2)+…+Р(Аn).
Два события называются совместными в данном опыте, если появление одного из них не исключает, появление другого в этом опыте. Так, при подбрасывании двух симметричных монет, события А - "герб на
верхней стороне первой монеты" и В - "цифра на верхней стороне второй монеты" являются совместными.
Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании. Например, несовместными являются попадание и промах при одном выстреле. Несколько событий называются несовместными, если они попарнонесовместны.
10.Теорема умножения вероятности.
Теорема: вероятность появления двух независимых событий равна произведению этих событий. P(A+B)=P(A)*P(B).
Теорема:
вероятность произведения конечного
числа независимых в совокупности
событий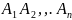 равна произведению вероятностей этих
событий.
равна произведению вероятностей этих
событий.
P(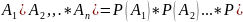 )
)
Теорема: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие произошло. P(AB)= P(A)*P(B/A)=P(B)*P(A/B)
Два события называются совместными в данном опыте, если появление одного из них не исключает, появление другого в этом опыте. Так, при подбрасывании двух симметричных монет, события А - "герб на
верхней стороне первой монеты" и В - "цифра на верхней стороне второй монеты" являются совместными.
Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании. Например, несовместными являются попадание и промах при одном выстреле. Несколько событий называются несовместными, если они попарнонесовместны.
Событие называется невозможным в данном опыте, если оно не может произойти в этом опыте. Так, если в ящике находятся только красные шары,ТО событие "из ящика извечен голубой шар" является невозможным (таких шаров в ящике нет).
Событие называется случайным в данном опыте, если оно может произойти, а может и не произойти в этом опыте. Например, если в ящике находятся n голубых и т красных шаров, одинаковы по размеру и весу, то событие "из урны извлечен голубой шар" является случайным (оно может произойти, а может и не произойти, поскольку в урне имеются не только голубые, но и красные шары). Случайными событиями являются "герб" и "цифра на верхней стороне монеты при ее подбрасывании", "попадание и промах при стрельбе по мишени", "выигрыш по билету лотереи" и Т.П.
