
- •Предмет теории вероятностей. Возникновение теории вероятностей.
- •Элементарные сведения из теории множеств.
- •Пространство элементарных событий. Случайные, достоверные, невозможные и несовместные события.
- •4. Действия над событиями (объединение, пересечение, разность).
- •2)Пересечение(произведение)-
- •5. Классическое определение вероятности.
- •6. Геометрическое определение вероятности.
- •7.Схема выбора без возвращения (сочетания, размещения).
- •8. Схема выбора с возвращением (перестановки, сочетания и размещения с повторением).
- •9.Теоремы сложения вероятности.
- •10.Теорема умножения вероятности.
- •11. Формула полной вероятности.
- •12.Формула Байеса.
- •13. Повторные независимые испытания.
- •Формула Бернулли. Наивероятнейшее число наступления события.
- •Наивероятнейшее число наступления события а в испытанмях Бернули
- •15.Локальная формула Муавра-Лапласа.
- •16.Интергральная формула Муавра-Лапласа.
- •17. Формула Пуассона
- •18.Случайная величина.
- •19 , 20.Дискретно распределённая случайная величина.
- •21.23 Непрерывно распределённая случайная величина.
- •22. Плотность распределения непрерывной случайной величины
- •24.Биномиальный закон распределения св.
- •25 . Распределение Пуассона св.
- •26.Нормальный закон распределение св (распределение Гаусса).
- •27. Геометрическое распределение случайной величины
- •28. 29Неравенство Чебышева.
- •30.Теорема Бернулли.
- •31.Генеральная и выборочная совокупность.
- •32 .Вариационный ряд
- •34.Эмперическая функция распределения.
- •36.Точечное оценивание параметров распределения.
- •34.Интервальное оценивание параметров распределения.
- •Критическая область, мощность критерия.
- •37. Схема проверки стат-ой гипотезы.
- •42. Основные понятия корреляционного и регрессионного анализа.
- •43)Линейная корреляционная зависимость и прямые регрессии
- •44)Коэффициент линейной корреляции и его свойства
4. Действия над событиями (объединение, пересечение, разность).
Объединением двух событий А и В называется событие С, состоящее в выполнении события А или события В, или обоих событий вместе.
Пересечением событий А и В называется событие, состоящее из элементарных событий принадлежащих и событию А и событию В.
Разность двух событий А и В называется событие, состоящее из элементарных событий, которые входят в событие А, но не входят в событие В.
Операции над событиями:
1)Объединение(Сумма)-это
А Ṳ В=А+В
ПР:А=(123…9)
В=(56…12)
АṲВ=(123….12)
2)Пересечение(произведение)-
А∩В=А*В
ПР: А=(123…9)
В=(56…12)
А∩В=(56…9)
3)Разность-
ПР: А=(123…9)
В =(56…12)
А/ В=(12…34)
5. Классическое определение вероятности.
Равнозначными событиями наз - если условия испытания обеспечивают одинаковую возможность осуществления , каждого из них.
Вероятность события называется отношение числа исходов благоприятствующих данному событию, к числу всех возможных исходов.
 .
где
m
- число элементарных исходов,
благоприятствующих событию А;
.
где
m
- число элементарных исходов,
благоприятствующих событию А;
n- число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Напр: Бросают 2 игральные монеты: Найти вероятность выпадения герба худобы один раз.
Ὼ{(гг)(рр)(рг)(гр)}
А=(Выпадает худобы один раз герб)
Р(А)=?
Р(А)=m/n=3/4
m=3
n=4
6. Геометрическое определение вероятности.
Геометрической вероятностью называют вероятность попадания точки в некоторую область (отрезок, часть плоскости).
 Пусть
отрезок l
составляет
часть отрезка L.
Пусть
отрезок l
составляет
часть отрезка L.
Пусть
отрезок L
наудачу поставлена точка. Тогда
вероятность, что эта точка попадет в
отрезок l
пропорциональна длине отрезка l;
не зависит от расположения l
на L.
И определяется по формуле:

В области G содержится область K, которая может имея Sk.
В область G на удачу бросается точка.
Пусть брошенная точка может попасть в некоторую часть G.
Требуется определение вероятности попадания этой точки в область K .
P(A)=Sk/Sg
7.Схема выбора без возвращения (сочетания, размещения).
Выборка без возвращения и без упорядочивания (Схема выбора проводящая к сочетанию)Суть выборки из n-элементов выбирает m-элемент выбирают без возвращения и без упорядочивания следования элементов.
Число сочетаний из n-элементов опред. След. Фор.
Схема выбора с возвращением (перестановки, сочетания и размещения с повторением).
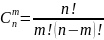

В магазин привезли мороженое 10 видов. Сколькими способами можно купить 6 различных пар мороженого.
n=10 m=6
С106 =10!/6!*(10-6)! =10!/6!*4!=7 8 9 10/1234=///
10!=1*2*3*4*5*6*7*8*9*10
Выборка без возвращения и c упорядочивания (Схема выбора проводящая к размещению)Суть выборки из n-элементов выбирает m-элемент выбирают без возвращения , но с упорядочивания следования элементов.
Число размещения из n-элементов по m-элементам опред. След. Фор.

ПР: Сколько всего существует телефонных номеров состоящих из 7 различных цифр.
n=10 m=7 А107=10!/(10-7)!=10!/3!=45678910=////
Основные правила и формулы комбинаторики
|
без возвращения |
с возвращением |
Без порядка |
|
|
С порядком |
|
|
Урновая
схема:

Выбор с возвр-нием:кажд выбр-ный шарик возвр-ся в урну, т.е. кажд из ак шариков выбир-ся из полной урны. В получ-м наборе, сост-м из ак номеров шариков, могут встреч-ся одни и те же номера (выборка с повторениями).
Выбор без возвр-ния:выбр-ные шарики в урну не возвр-ся, и в получ наборе не могут встреч-ся одни и те же номера (выборка без повторений).
Выбор с учетом порядка:два набора номеров шариков считаются различными, если они отличаются составом или порядком номеров.
Выбор без учета порядка:два набора номеров шариков считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми.


