§3.5. Четвертый тип диаграмм. Компоненты а и в образуют прочные химические соединения, устойчивые вплоть до температуры плавления.

Диаграмма состояния системы, где компоненты образуют одно химическое соединение А_mB_n представлена на рисунке. Точка С соответствует составу химического соединения А_mB_n постоянного состава. Избыток любого из компонентов (А или В) понижает температуру плавления соединения. Именно поэтому температура его плавления является наиболее высокой, что отражает наличие максимума на линии ликвидус. Если сделать разрез по линии С- А_mB_n, то диаграмму можно рассматривать как сочетание двух диаграмм первого типа для систем А- А_mB_n и А_mB_n-В, в которых полностью отсутствует растворимость в твердом состоянии.

Поскольку химическое соединение А_mB_n обладает собственной температурой плавления, то кривая охлаждения для сплава, проходящего непосредственно по ординате химического соединения абсолютно аналогична кривой охлаждения для чистого компонента.

Соединения, в которых отношение между количествами компонентов выражается целыми числами, называются стехиометрическими или дальтонидами, так как они удовлетворяют закону кратных отношений, открытому Дальтоном.

Из данного рисунка видно, что химическое соединение, образованное компонентами А и В, может содержать их в отношениях несколько отличающихся от соответствующих A_mB_n, т.е. на диаграмме имеется более или менее обширная область существования однородной фазы на основе этого соединения, ограниченная кривыми ab, bC, Cd и de – так называемая область гомогенности.

Слева от вертикальной штриховой линии в химическом соединении имеется дефицит атомов В, а справа – атомов А. Такие соединения были названы бертоллидами в честь французского химика Бертолле. Можно так же сказать, что эти соединения нестехиометрические. Следует отметить, что кривая охлаждения для сплава, проходящего через точку С будет иметь точно такой же вид как и кривая для стехиометрического химического соединения A_mB_n.

§3.6. Пятый вид диаграмм. Компоненты а и в образуют непрочное соединение, разлагающееся ниже температуры плавления.

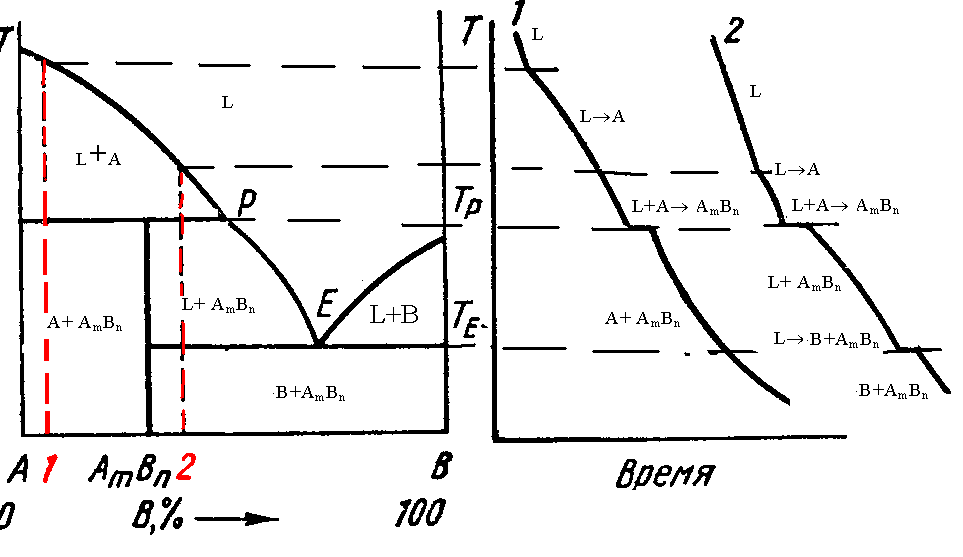
Из-за неустойчивости химического соединения оно не может выделяться при температурах выше Т_р. При температурах ниже Т_р оно образуется по перитектической реакции L+A A_mB_n. Так же как в случае устойчивого химического соединения, неустойчивое соединение может быть стехиометрическим и нестехиометрическим.

§3.7. Пример.

1. Для каждой области диаграммы назовите присутствующие фазы.

2. Определите концентрации (в атомных процентах) каждого компонента в сосуществующих фазах для системы, содержащей 20 ат.% V при температуре 1230С.

3. Нарисуйте кривые охлаждения и опишите процессы, происходящие при охлаждении систем, содержащих 5 и 60 ат.% V.

4. Рассчитайте массу каждой фазы и массу каждого компонента в каждой фазе для системы, содержащей 20 ат.% V при температуре 1000С, если общая масса системы 100 грамм.

5. Рассчитайте сколько грамм и какого компонента в минимальном количестве необходимо добавить в систему, содержащую 10 ат.% Zr при температуре 1600С, чтобы она из двухфазной превратилась в однофазную при той же температуре, если масса всей системы равна 200 грамм.

6. Определите число термодинамических степеней свободы в точках, указанных на диаграмме.

Перед Вами реальная диаграмма Zr-V. Разберем последовательно все пункты задания.

Но прежде следует обратить внимание на то, что данная диаграмма имеет две шкалы. Построена диаграмма в атомных процентах и на нижней шкале отложены атомные проценты, а необходимая для выполнения некоторых заданий шкала весовых процентов нанесена сверху. Она неравномерна, в отличие от равномерной шкалы атомных процентов.

1. Для каждой области диаграммы назовите присутствующие фазы.

В этом пункте кроме определения, какие фазы существуют в той или иной области хорошо бы определить типы реакций, протекающих на горизонталях, типы химических соединений, если таковые имеются, растворимость компонентов друг в друге в твердом состоянии, если таковая имеется.

Расстановку фаз начинают с того, что находят все однофазные области, которые есть на диаграмме. Как видно из вышеизложенного вариантов всего три. Это область, в которой существует расплав (L), всегда находящаяся выше линии ликвидус; области твердых растворов на основе компонентов и нестехиометрические химические соединения. На данной диаграмме таких однофазных областей всего три.

Область I, область жидкого расплава – ее мы обозначили L.

Область II – область твердого раствора на основе циркония или твердый раствор ванадия в цирконии. Растворимость твердого V в твердом Zr составляет 16,5 ат.% V или 10 вес.% V. Эти проценты обычно наносят на диаграмму и здесь они нанесены под точкой а, это крайняя левая точка горизонтали при температуре 1230С.

Область III - область твердого раствора на основе ванадия или твердый раствор циркония в ванадии. Максимальная растворимость циркония в ванадии определяется точкой n, это крайняя правая точка горизонтали при 1300С.

Нестехиометрических химических соединений в этом случае нет, зато есть одно стехиометрическое ZrV₂. Поскольку оно не имеет точки плавления, а образуется по перитектической реакции – неустойчивое химическое соединение. Его состав 67 ат.%V и 33 ат.% Zr. Зная состав химического соединения в атомных процентах, легко определить формулу химического соединения, если она неизвестна. Делают это так: . Таким образом, на 1 атом Zr приходится 2 атома V, следовательно, имеем формулу ZrV₂.

Теперь определяем, какие фазы сосуществуют в двухфазных областях. Для того чтобы это определить, достаточно посмотреть, что ограничивает двухфазную область справа и слева. Это могут быть либо однофазные области, либо ординаты чистых компонентов и химических соединений.

Область IV слева ограничена однофазной областью , справа однофазной областью L. Имеем: + L.

Область V аналогична IV, только справа она ограничена однофазной областью . В области V – +L.

Область VI слева ограничена однофазной областью L, справа ординатой химического соединения ZrV₂. В области L+ ZrV₂.

Область VII – слева – однофазная область, справа – ордината ZrV₂. В области  + ZrV₂.

Область VIII – слева – ордината чистого Zr, справа - . В области  + Zr.

Область IX – слева - ордината ZrV₂, справа - . В области + ZrV₂.

Область X – ограничена двумя ординатами. Слева – чистого Zr, справа - ZrV₂. В области механическая смесь твердых кристаллов Zr + ZrV₂.

Далее определим, какие реакции протекают на горизонталях, присутствующих на диаграмме. Это полезно сделать, потому что при выполнении остальных заданий может понадобиться, как, например, при построении кривых охлаждения.

Всего существует 4 типа реакций: эвтектическая, эвтектоидная, перитектическая, перитектоидная. С перитектоидной реакцией в нашем курсе Вы не встретитесь. С эвтектической и перитектической встречались при рассмотрении простых диаграмм. Довольно часто попадается и эвтектоидная.

Как отличить, где протекает та или иная реакция на диаграмме?

Эвтектическая и эвтектоидная реакции протекают на горизонталях, над которыми линии ликвидус или солидус образуют воронку.

В результате и эвтектической, и эвтектоидной реакций получается механическая смесь двух твердых фаз. Это могут быть твердые растворы, химические соединения, чистые компоненты. Только по эвтектической реакции эта смесь получается из жидкости, а по эвтектоидной из твердого раствора.

Lтвердое1+твердое2 – эвтектическая. твердое1+твердое2 – эвтектоидная.

П еритектическая реакция, в основном, появляется в случае образования неустойчивого химического соединения (и стехиометрического и нестехиометрического). По виду напоминает букву Т (в случае стехиометрического соединения) или букву Т с толстой ножкой (в случае нестехиометрического). В области, находящейся над перитектической горизонталью всегда присутствует жидкий расплав (L) и твердое вещество (может быть: твердый раствор, чистый компонент или другое химическое соединение). По перитектической реакции из смеси расплава и твердого получается химическое соединение.

L+твердоеA_mB_n (или ).

На диаграмме Zr-V присутствуют все три типа реакций.

При температуре 1300С – перитектическая +LZrV₂.

При температуре 1230С – эвтектическая L+ ZrV₂.

При температуре 777С – эвтектоидная Zr+ ZrV₂.

2. Определите концентрации (в атомных процентах) каждого компонента в сосуществующих фазах для системы, содержащей 20 ат.% V при температуре 1230С.

Определить концентрации компонентов в сосуществующих фазах – это значит определить сколько атомных процентов каждого из компонентов содержится в той или иной фазе.

Данная нам точка попадает на эвтектическую горизонталь. Поскольку здесь протекает реакция L+ ZrV₂, то мы должны определить состав трех сосуществующих фаз (L,  и ZrV₂).

Состав -фазы определяется точкой а. Здесь 16,5 ат.% V и 83,5 ат.% Zr.

Состав жидкости определяется точкой Е. В ней 43,5 ат.% V и 56,5 ат.% Zr.

Состав ZrV₂ определяется точкой d. Мы уже определяли этот состав: 67 ат.% V и 33 ат.% Zr.

Если взять тот же процент ванадия, но попросить определить состав сосуществующих фаз, например, при1400С, то мы будем определять состав уже двух фаз, тех которые существуют в этой области: L и . Для того, чтобы определить состав необходимо провести коноду через заданную точку (см. диаграмму). Состав -фазы будет определяться точкой, лежащей на линии солидус (f), состав жидкости – точкой, лежащей на линии ликвидус (m). Состав -фазы: 12 ат.% V и 88 ат.% Zr. Состав жидкости: 34 ат.% V и 66 ат.% Zr.

3. Нарисуйте кривые охлаждения и опишите процессы, происходящие при охлаждении систем, содержащих 5 и 60 ат.% V.

На рисунке представлены кривые охлаждения. Для того чтобы описать процессы, происходящие при охлаждении сплавов, достаточно написать на самой кривой какие процессы протекают и какие фазы охлаждаются.

Кривая для сплава, содержащего 5 ат.% V. До температуры Т₁ охлаждается жидкость. В этой точке начинается выделение твердых кристаллов  (на кривой наблюдается излом), которое продолжается до температуры Т₂, здесь исчезают последние капли жидкости (заканчивается излом) и далее до температуры Т₃ происходит охлаждение твердой -фазы. В точке 3 из -фазы выделяются кристаллы Zr (наблюдается второй излом) до температуры Т₄. Точка 4 находится на горизонтали нонвариантного эвтектоидного превращения (Zr+ ZrV₂), на кривой охлаждения наблюдается площадка. Ниже температуры Т₄ охлаждается механическая смесь кристаллов Zr и ZrV₂.

Кривая для сплава, содержащего 60 ат.% V строится аналогично. Ордината этого сплава пересекает все три горизонтали, присутствующие на этой диаграмме. Следовательно, на кривой охлаждения будет три площадки.

4. Рассчитайте массу каждой фазы и массу каждого компонента в каждой фазе для системы, содержащей 20 ат.% V при температуре 1000С, если общая масса системы 100 грамм.

Найдя эту точку, попадаем в область, в которой сосуществуют две фазы  и ZrV₂. Найдем их массы по правилу рычага. Напоминаем, что решать задачу с помощью правила рычага можно только, выражая состав фаз в весовых процентах.

Проведем через данную точку коноду и определим весовой процент ванадия и циркония в каждой точке.

По правилу рычага  гр.

 гр.

Можно себя проверить. В сумме массы двух фаз должны давать массу сплава (в нашем случае 100 гр.). Действительно, 90,9+9,1=100 гр.

Теперь рассчитаем массы каждого компонента в каждой фазе.

1. Масса ванадия в -фазе. Содержание ванадия в -фазе составляет 8 вес.%, следовательно, если умножить массу фазы на весовую долю компонента в этой фазе, мы найдем массу компонента в данной фазе.

гр.

2. Масса циркония в -фазе. Содержание циркония в -фазе 92 вес.%.

гр.

3. Масса ванадия в ZrV₂. Содержание ванадия в этой фазе – 52 вес.%.

гр.

4. Масса циркония в ZrV₂. Содержание циркония в этой фазе – 48 вес.%.

гр.

Тоже можно себя проверить. Сложив массы двух компонентов, получим массу фазы, в которой искали их. Сложив массы всех четырех компонентов найдем массу сплава.

5. Рассчитайте сколько грамм и какого компонента в минимальном количестве необходимо добавить в систему, содержащую 10 ат.% Zr при температуре 1600С, чтобы она из двухфазной превратилась в однофазную при той же температуре, если масса всей системы равна 200 грамм.

Находим эту точку. Следует обратить внимание, что здесь задание дано не в процентах ванадия, а в процентах циркония. 10 ат.% Zr - это 90 ат.% V. Таким образом мы попадем в область, обозначенную на диаграмме цифрой V. Также как в предыдущей задаче, проведем коноду и определим весовые проценты в каждой точке.

В средней точке мы имеем две фазы. Если мы переместимся вправо, то попадем в однофазную область , и будем добавлять V. Если будем перемещаться влево, то попадем в жидкость, и будем добавлять Zr. В задаче сказано «в минимальном количестве», это означает, что достаточно посчитать, сколько компонента надо добавить, чтобы перейти на линию ликвидус или солидус, или ординату химического соединения.

Исходный сплав содержит 83 г V в 100 г раствора (по определению весового процента). Но у нас 200 г раствора, значит и ванадия в нем будет в два раза больше – 166 г. Если мы добавляем X грамм V к 166 г V, содержащемся в растворе, то и вся масса раствора увеличивается на X г. Добавив такое количество V, получаем новый сплав, содержащий 94 г V в 100 г раствора.

Все эти рассуждения можно записать в виде простой пропорции:

166+X  200+X

94  100

Решаем пропорцию:

(166+X)^.100=94^.(200+X)

6X=2200

X=366,7 г ванадия

Аналогично рассуждаем в случае добавления Zr.

Исходный сплав содержит 17 г Zr в 100 г раствора или 34 г в 200 г раствора. Если мы добавляем Y грамм Zr к 34 г Zr, содержащемся в растворе, то и вся масса раствора увеличивается на Y г. Добавив такое количество V, получаем новый сплав, содержащий 38 г Zr в 100 г раствора.

34+Y  200+Y

38  100

Решив уравнение, получаем, что добавить надо 67,7 г циркония.

Итак, чтобы система превратилась из двухфазной в однофазную при постоянной температуре надо добавить или 366,7 г ванадия, или 67,7 г циркония.

6. Определите число термодинамических степеней свободы в точках, указанных на диаграмме.

Число компонентов на двухкомпонентной диаграмме может быть только два или один.

Один компонент - в случае если точка принадлежит ординате чистого компонента или ординате химического соединения (в этом случае само химическое соединение считается компонентом), в том числе и воображаемой ординате нестехиометрического химического соединения.

Число фаз – может быть одна, две или три.

Одна фаза – однофазные области; ординаты чистых компонентов и химических соединений, исключая точки плавления и фазовых превращений.

Две фазы – двухфазные области; точки плавления и точки фазовых переходов чистых компонентов и химических соединений.

Три фазы – любая горизонталь, где протекает эвтектическое, эвтектоидное, перитектическое или перитектоидное превращения.

При определении количества фаз действует правило: вертикаль главнее горизонтали, т.е. в месте пересечения вертикали и горизонтали – точка принадлежит горизонтали.

Рассчитаем числа степеней свободы в точках, указанных на диаграмме.

Точка 1. К=1 (Zr), Ф=2 (Zr-твердый, Zr-жидкий), С=1-2+1=0.

Точка 2. К=1 (Zr), Ф=2 (Это точка фазового перехода, т.е. до этой температуры кристаллизуется одна модификация твердого циркония, допустим -Zr, а в этой точке он превращается, скажем, в -Zr. Поэтому фаз две), С=1-2+1=0.

Точка 3. К=1 (Zr), Ф=1 (Zr-твердый), С=1-1+1=1.

Точка 4. К=2 (Zr, V), Ф=2 (L, ), С=2-2+1=1.

Точка 5. К=2 (Zr, V), Ф=3 (L, , ZrV₂), С=2-3+1=0.

Точка 6. К=2 (Zr, V), Ф=3 (Zr, , ZrV₂), С=2-3+1=0.

Точка 7. К=1 (ZrV₂), Ф=1 (ZrV₂ - твердый), С=1-1+1=1.

Точка 8. К=2 (Zr, V), Ф=3 (L, , ZrV₂. Хотя эта точка и лежит на пересечении вертикали и горизонтали, но она принадлежит горизонтали, т.к. сначала должно произойти перитектическое превращение, в результате которого образуется химическое соединение), С=2-3+1=0.

Точка 9. К=2 (Zr, V), Ф=2 (, ZrV₂), С=2-2+1=1.

Точка 10. К=2 (Zr, V), Ф=1 (), С=2-1+1=2.

Точка 11. К=2 (Zr, V), Ф=1 (L), С=2-1+1=2.