§3.2. Правило рычага.

При помощи диаграмм состояния можно определить соотношение между весовыми количествами сосуществующих фаз для сплава данного состава при данной температуре.

Правило рычага можно использовать только для двухфазной области.

Чтобы можно было воспользоваться правилом рычага необходимо, чтобы на диаграмме была шкала весовых процентов.

Возьмем два сплава (1 и 2) при некоторой температуре Т. Пересечение ординат сплавов и заданной температуры даст нам точки b и c. Проведем горизонтальную линию до пересечения с линиями диаграммы. Такая горизонталь называется конодой.

Для сплава 1 определим массы сосуществующих фаз. Это фазы: жидкость и твердые кристаллы А.

По правилу рычага соотношение масс жидкой и твердой фаз можно записать таким образом: . Можно отнести массу каждой фазы к массе сплава, которая обязательно будет задана в задаче, тогда: и .

Для сплава 2 – аналогично. . Также и .

Отсюда видно, чем ближе сплав к эвтектическому, тем больше доля жидкой фазы при данной температуре.

Пример1.

Сколько граммов золота находится в жидкой фазе сплава, содержащего 30 вес.% Au, при температуре 800С, если масса сплава 400 г. На диаграмме указаны весовые проценты.

Найдем точку на диаграмме, проведем коноду до пересечения с линией ликвидус, определим весовые проценты. Коноду можно схематически нарисовать – это более удобно.

По правилу рычага массе жидкой фазы (L) будет соответствовать отрезок ab, а массе всего сплава – отрезок ad.

Таким образом, массу жидкости можно вычислить:

г.

Массу золота в жидкости можно вычислить так:

г.

Расчет числа степеней свободы

Рассчитаем число степеней свободы для точек, указанных на диаграмме.

С=К-Ф+1

Точка 1 – точка плавления компонента А.

Компонент -1 (чистый А), а фаз две – чистый твердый А и жидкий А. Тогда С=1-2+1=0.

Точка 2 – компонентов -2 (А и В) и фаз – 2, т.к. в этой точке уже присутствуют первые кристаллы А. С=2-2+1=1.

Точка 3 – компонентов - 2 (А и В), а фаза 1 (L). С=2-1+1=2.

Точка 4 – аналогична точке 2. Компоненты – А и В, фазы – L и А. С=2-2+1=1.

Точка 5 – принадлежит эвтектической горизонтали, протекает реакция LA+B. Таким образом, компонентов – 2 (А и В), а фаз – 3, те которые участвуют в реакции (L, A, B). С=2-3+1=0.

Точки 6 и 7 аналогичны точкам 2 и 4. С=2-2+1=1.

Точка 8 аналогична точке 1, только это точка плавления компонента В, а не А. С=1-2+1=0.

Точка 9 – компонент -1 (В), фаза тоже одна (твердый В). С=1-1+1=1.

Точка 10 аналогична точке 9 – 1 компонент (А) и одна фаза (твердый А). С=1-1+1=1.

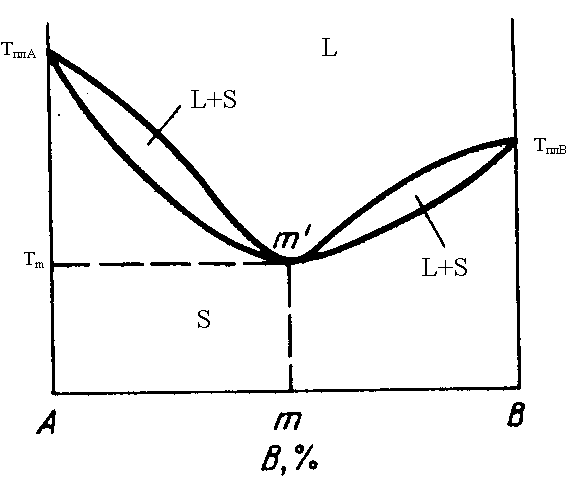
§3.3. Второй тип диаграмм. Компоненты а и в неограниченно растворимы друг в друге как в жидком, так и в твердом состоянии и не образуют между собой химических соединений.

Системы такого типа обычно образуются близкими по своей природе компонентами (например, Sb-Bi, Au-Ag и т.д.).

Верхняя линия диаграммы, так же как и в первом типе – линия ликвидус. Выше нее существует только жидкость. Нижняя линия – линия солидус. Ниже нее существует только твердая фаза. В данном случае мы обозначили ее S. Это непрерывный ряд твердых растворов компонентов друг в друге (обычно это твердые растворы замещения).

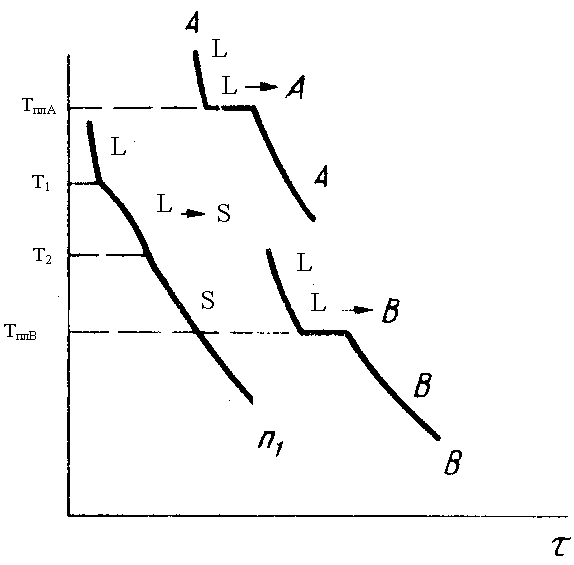
Кривые охлаждения были построены для трех сплавов. Для чистого А, чистого В и n₁, находящегося посередине.

Кривые охлаждения для чистых компонентов аналогичны рассмотренным для первого типа диаграмм, они имеют одну площадку при температуре плавления компонентов. При охлаждении расплава n₁ до температуры Т₁ начинается кристаллизация твердого раствора, и охлаждение замедляется (перегиб на кривой). После окончания кристаллизации (состав твердой фазы совпадает с исходным составом жидкости) скорость охлаждения вновь увеличивается и на кривой появляется второй излом. Кривые охлаждения всех сплавов в этой системе подобны друг другу и различаются только температурами начала и конца кристаллизации.

В тех случаях, когда компоненты имеют близкие температуры плавления, диаграммы равновесия рассмотренного типа часто характеризуются наличием максимумов и минимумов. Сплав, который имеет состав, отвечающий точке экстремума, кристаллизуется при постоянной температуре без изменения состава.