§17. Термодинамические функции: энергия Гиббса и энергия Гельмгольца.

В изолированных системах энтропия может только увеличиваться при необратимых процессах и при равновесии достигать максимума. Поэтому ее можно использовать для суждения о направлении процессов в изолированной системе. Однако на практике большинство процессов протекает в неизолированных системах. Действие почти всех промышленных агрегатов связано с теплообменом и изменениями объема. Поэтому для таких незамкнутых систем целесообразно выбрать другие критерии равновесия. Возможность или невозможность процессов при этом связывается с работой, которую они могут произвести. Т.К. работа зависит от пути процесса, то ее нельзя выбрать в качестве критерия. Но если ограничить рассмотрение частным случаем процесса при постоянной температуре, то максимальная работа при его обратимом протекании определяется изменением некоторой функции состояния.

(15)

Уравнение (15) носит название объединенного уравнения I и II законов термодинамики.

(16)

Уравнение (16) вводит новую функцию состояния А – свободную энергию при постоянном объеме или энергию Гельмгольца.

При обратимом изотермическом процессе работа равна убыли некоторой функции состояния A=U-TS, называемой свободной энергией при постоянном объеме.

Убыль свободной энергии при обратимом изотермическом процессе равна произведенной работе.

Если к условию постоянства температуры добавить условие постоянства объема, т.е. , то получим

или

.

Отсюда следует, что при постоянных температуре и объеме свободная энергия не изменяется при обратимых процессах, а при необратимых может только убывать. Это означает, что функция А является критерием, который позволяет судить о направлении процессов в незамкнутых системах. Очевидно, для таких систем условием равновесия является минимум свободной энергии (при V и T=const).

В технике большинство процессов совершается при постоянном давлении. Поэтому кроме свободной энергии при постоянном объеме целесообразно ввести такую функцию состояния, которая служила бы критерием равновесия в условиях постоянства давления и температуры.

Если объем системы изменяется, то

При постоянстве давления:

.

Таким образом, новая функция состояния G называющаяся свободной энергией при постоянном давлении (энергией Гиббса, изобарно-изотермическим потенциалом) определяется уравнением:

.

При обратимых процессах величина энергии Гиббса не изменяется, а при необратимых может только убывать. Следовательно, условием равновесия в системах при постоянных p и T является минимум энергии Гиббса.

Может быть более наглядной будет связь между различными функциями состояния, если изобразить ее графически.

§18. Зависимость свободной энергии и энтропии от параметров состояния.

Найдем выражения для функций A и G одного моля идеального газа. Из определения теплоемкости при постоянном объеме следует, что

,

где U₀ – внутренняя энергия тела при абсолютном нуле.

A=U-TS

Энтропия идеального газа при постоянной температуре растет с увеличением объема и уменьшается при увеличении давления.

,

где I – постоянная интегрирования.

,

где - постоянная величина, зависящая только от температуры. Заменяя , получим

Т.к. G=A+pV, то для идеального газа G=A+RT.

Введя RT в функцию D’(T), находим, что

G=L(T)+RTlnp.

Величину L(T) часто обозначают через G⁰.

Функции A и G широко используются для анализа возможности различных процессов и реакций.

Пусть, например, мы хотим выяснить, возможно ли превращение графита в алмаз при данных p и T. Если G_{(алмаза)}>G_{(графита)}, то G= G_{(алмаза)}- G_{(графита)}>0, такой процесс невозможен. Однако для других p и T знак величины G может измениться на обратный. Действительно, сейчас этот процесс осуществляется при Т≈3000 К и р≈100000 атм.

Для решения большого числа подобных задач необходимо знать зависимость функций A и G от T, V и p.

A=U-TS

Продифференцировав это уравнение:

dA=dU-TdS-SdT

и подставив в него значение TdS=Q=dU+pdV, получим

dA=-pdV-SdT.

Это уравнение дает зависимость энергии Гельмгольца от V и T.

(17)

(18)

Дифференцируя уравнение G=U-TS+pV, получим:

dG=dU-TdS-SdT+pdV+Vdp.

Подставляя значение TdS, получаем

dG=Vdp-SdT.

Откуда следует, что

(19)

(20)

Подставив выражения из уравнения (18) и (20) в выражения для энергии Гиббса и энергии Гельмгольца, получим:

(21)

(22)

Уравнения (21) и (22) носят название уравнений Гиббса-Гельмгольца. Они дают зависимость свободной энергии при постоянном объеме (энергии Гельмгольца) и при постоянном давлении (энергии Гиббса) от температуры для однородного вещества. Эти уравнения могут быть представлены в более удобном виде, так разделив обе части уравнения на Т², получим:

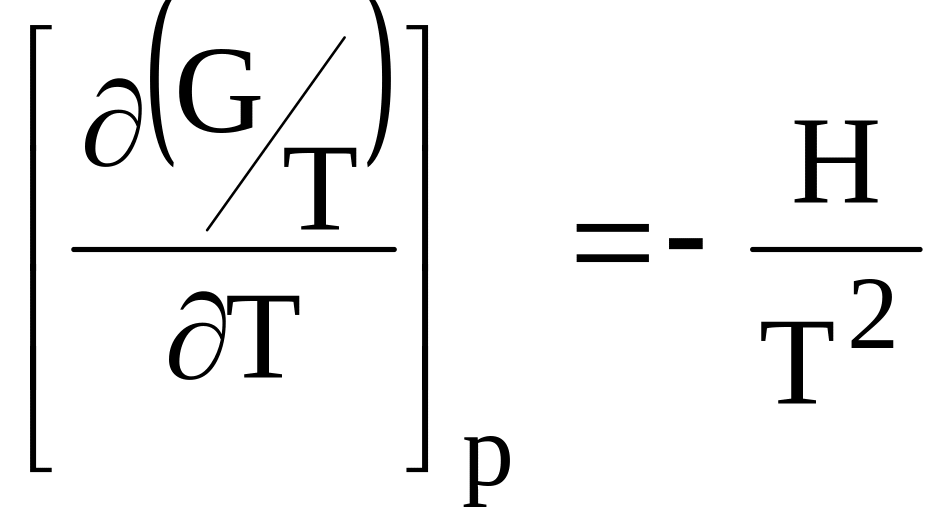(23)

или (24)

Уравнения (21), (22), (23) для изменений функций A и G, т.е. для процессов, принимают вид:

.

Еще раз об определении направления процесса в различных системах:

для изолированных систем:

dS0 знак = относится к равновесному состоянию

> к самопроизвольным процессам

для неизолированных систем:

при T и V – const

dA0 самопроизвольно могут протекать только те процессы, которые сопровождаются уменьшением энергии Гельмгольца, причем пределом их протекания является достижении е некоторого минимального значения энергии Гельмгольца для данных условий (или при A<0 – возможен самопроизвольный процесс, при A>0 возможен обратный процесс, а при A=0 – состояние равновесия).

при T и р – const

dG0 самопроизвольно могут протекать только те процессы, которые сопровождаются уменьшением энергии Гиббса, причем пределом их протекания является достижении е некоторого минимального значения энергии Гиббса для данных условий (или при G<0 – возможен самопроизвольный процесс, при G>0 возможен обратный процесс, а при G=0 – состояние равновесия).