§16. Примеры решения задач.

Пример 1.

Найдите изменение энтропии при переходе 1 моля азота от 25С и неизвестного объема к 200С и V₂=50 л. p=const.

Эту задачу можно решить двумя способами. Можно воспользоваться условием, что давление постоянно, но тогда возникает вопрос, а зачем дан объем?

Можно решить задачу, разложив на две: сначала рассмотреть изохорический нагрев, а потом изотермическое расширение.

Решим двумя способами и убедимся, что результат будет одинаковым.

Способ 1.

p=const. Дж/К

Азот газ двухатомный, поэтому С_V=5/2R, а С_p=C_v+R=7/2R

Способ 2.

1. Изохорический нагрев

Дж/К

2. Прежде чем рассматривать изотермическое расширение, надо найти неизвестный первый объем. Это можно сделать, воспользовавшись условием, что давление постоянно и уравнением Менделеева-Клайперона.

л.

Дж/К

Дж/К

Как видно из решения, обоими способами получился одинаковый результат. Это возможно, поскольку энтропия является функцией состояния.

Пример 2.

Вычислите изменение энтропии, происходящее при расширении до 1000 см³ и одновременном нагревании до 100С аргона, содержащегося в сосуде, объемом 500 см³ при 25С и начальном давлении 1 атм.

Задача похожа на предыдущую, но из условия ясно, что постоянного параметра нет. Меняется и температура, и давление, и объем. В таком случае решаем задачу вторым способом, т.е. сначала рассчитываем изотермическое расширение, потом изохорическое нагревание, а можно изотермическое расширение и изобарический нагрев, результат будет одинаковым.

Сначала найдем число молей аргона, для этого нам дано давление 1 атм. Воспользуемся уравнением Менделеева-Клайперона.

моля

Изобразим процесс графически, чтобы было нагляднее.

1. Дж/К

2. Дж/К

Поскольку аргон – одноатомный газ, принимаем C_V=3/2R.

3. Дж/К

Пример 3.

Два моля идеального одноатомного газа при начальном давлении 1 атм. и температуре 300 К были проведены через следующий цикл, все стадии которого обратимы:

I – изотермическое сжатие до 2 атм.

II – изобарическое нагревание до 400 К.

III – возвращение в исходное состояние.

Изобразите цикл графически и определите изменение энтропии на каждой стадии.

1. Процесс изотермический.

Дж/К

2. Процесс изобарический.

Дж/К

Поскольку газ одноатомный, принимаем С_V=3/2R, C_p=C_V+R.

3. Поскольку энтропия функция состояния изменение энтропии всего процесса в целом будет равно нулю, т.к. начальное и конечное состояние системы – это одна и та же точка.

Дж/К

Пример 4.

Вычислить изменение энтропии при нагреве 20 г индия от 25С до 500С, если индий плавится при температуре 430 К и Н_пл=3,283 кДж/моль.

С_р(тв)=18,297+24,172^.10^-3Т

С_р(ж)=27,456+1,092^.10^-3Т

Изменение энтропии при нагреве индия от 25С до 500С будет складываться из трех частей.

1. Изменение энтропии при нагреве твердого In от 25С (298 К) до Т_пл=430 К.

А_In=115 г/моль

Число молей индия: моль

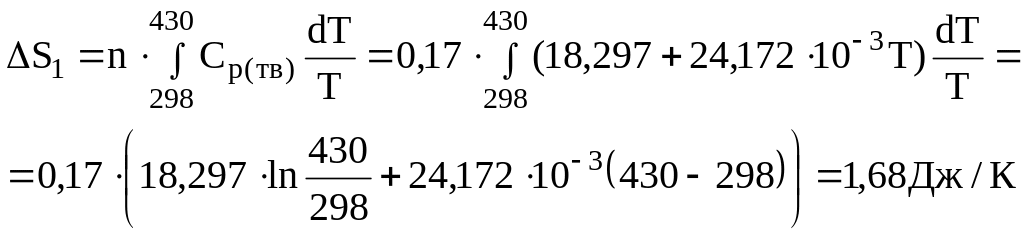
2. Изменение энтропии при плавлении:

3. Изменение энтропии при нагреве жидкого In от Т_пл=430 К до 500С (773 К).

S=S₁+S₂+S₃=1,68+1,3+2,8=5,78 .

Пример 5.

Рассчитайте изменение энтропии при реакции 2H_2(газ)+СО_(газ)=СН₃ОН_(газ) при температуре 500 К с помощью таблиц стандартных термодинамических величин.

	Н2	СО	СН3ОН
S298, Дж/моль.К	130,6	197,4	239,7
а	27,28	28,41	15,28
b.103	3,26	4,10	105,2
c'.10-5	0,502	-0,46	-
c.106	-	-	-31,04

Изменение энтропии реакции в стандартных условиях:

Дж/К

а = 15,28-28,41-2^.27,28 = - 67,69

b = 105,2-4,10-2^.3,26 = 94,58

с’=0,46-2^.0,502 = -0,544

с = -31,04

С_p= -67,69+94,58^.10^-3.Т-0,544^.10⁵Т^-2-31,04^.10^-6Т²

Пример 6.

Молярная теплоемкость сероводорода (H₂S) равна С_р=29,4+0,0154^.Т Дж/моль^.К. Вычислите молярную энтропию H₂S при 227С и давлении 2 атм., если Дж/моль^.К.

Стандартная энтропия изменится на S при изобарическом нагревании и S при изотермическом сжатии.

Тогда: