Энергетический спектр электронов и плотность электронных состояний в низкоразмерных объектах

Важнейшие квантовомеханические характеристики тел - это энергетически спектр электронов E и плотность квантовых состояний g(Е). Эти характеристики определяют электронные свойства объекта и реакцию на внешние воздействия.

Энергетический спектр – это совокупность возможных значений энергии частицы в данных условиях. Если энергия квантуется, то энергетический спектр называется дискретным. Если энергия может принимать непрерывный ряд значений, то спектр называется сплошным (непрерывным).

Плотность состояний g(Е) – это число квантовых состояний электронов на единицу объема, площади или длины (в зависимости от размерности объекта), отнесенное к единичному интервалу энергий:

,

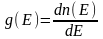где dn(E) – число возможных состояний в интервале энергий от E до E + dE. Знание плотности состояний g(Е) и вероятности их заполнения электронами f(Е) позволяет установить распределение электронов рассматриваемой системы по квантовым состояниям и описать электрические, оптические и некоторые другие свойства системы.

Электроны обладают полуцелым спином , поэтому вероятность заполнения ими квантовых состояний определяется статистикой Ферми-Дирака и подчиняется принципу Паули.

Энергетический спектр 3d-электронного газа

В неограниченном кристалле электроны могут свободно двигаться в любом направлении. Энергия электрона

,

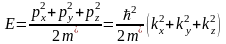где p и k - квазиимпульс и квазиволновой вектор электрона.

В пределах зоны проводимости величина E может принимать практически непрерывный ряд значений. Расстояние между соседними уровнями в энергетической зоне 10^-22 эВ.

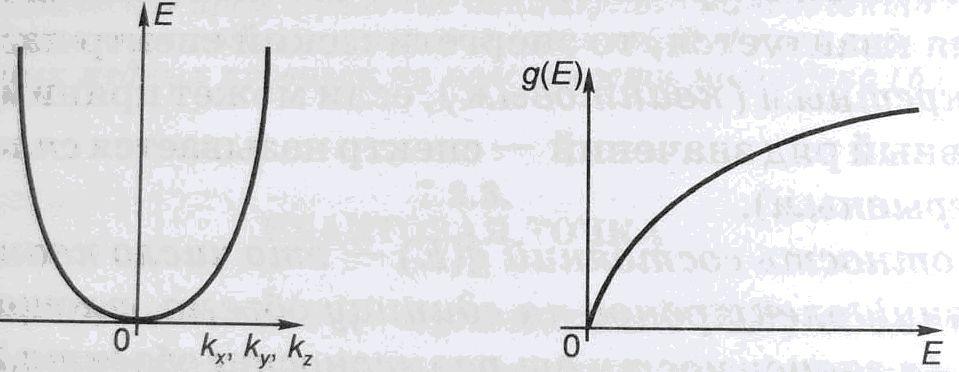
График функции g(Е) - парабола:

g(Е) = CE^1/2.

Плотность состояний мала у дна зоны и увеличивается с ростом Е. В пределах одной энергетической зоны функции E(k_x, k_y, k_z) и g(Е) непрерывны, поэтому электронные свойства 3D-кристалла под влиянием внешних воздействий изменяются непрерывно.

Энергетический спектр 2d-электронного газа

Квантовая яма (2D-электронный газ). Движение электронов ограничено отрезком d_y в направлении оси y. Энергия движения в направлении y квантуется (одномерная бесконечно глубокая потенциальная яма ширины d_y):

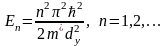
Движение характеризуется единственным квантовым числом n. Если яма бесконечно глубока, то на ее ширине d_y укладывается целое число _n/2. Устойчивым состояниям электрона соответствует стоячая волна, образованная падающей и отраженной от стенок ямы волной де Бройля. Величины E_n называются квантоворазмерными уровнями.

Энергия движений вдоль осей x и z не квантуется и определяется такими же выражениями, как для свободной частицы. Полная энергия электрона:

.

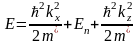Энергетический спектр электрона в квантовой яме двухмерного нанообъекта дискретно-непрерывный. Каждому размерному уровню E_n соответствует множество возможных значений E (подзона) за счет свободного движения электрона вдоль осей x и z. Эта совокупность энергий называется двухмерной подзоной размерного квантования.

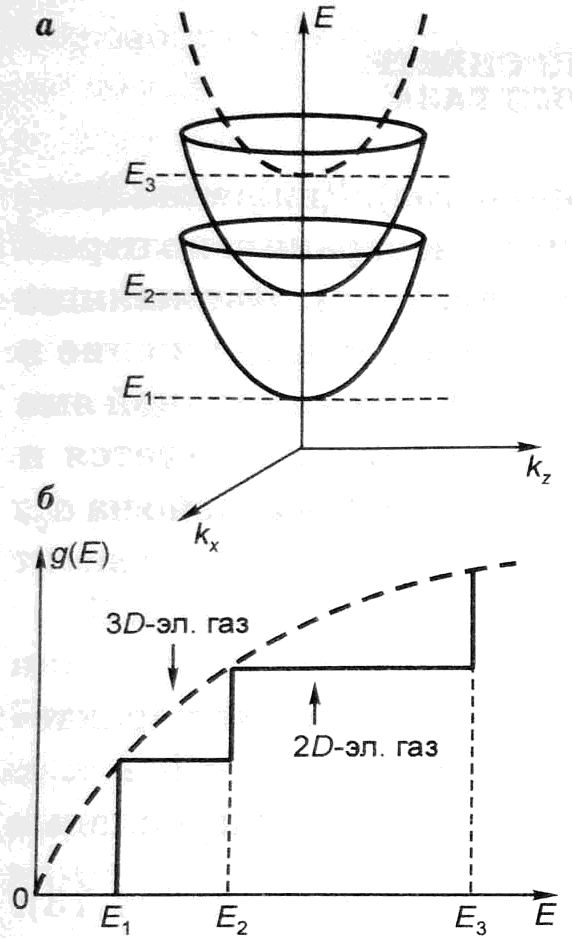
График зависимости E(k_x, k_z) – система параболоидов; дно n-го параболоида соответствует уровню E = E_n.

Зависимость g(Е) имеет ступенчатый характер. Каждая размерная подзона вносит одинаковый вклад, равны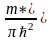й , в величину плотности состояний.

Строго говоря, модель бесконечно глубокой прямоугольной потенциальной ямы справедлива только для движения электрона в тонкой пленке при наноразмерной толщине d. Индивидуальную протяженную плоскопараллельную пленку нанометровой толщины реализовать трудно. На практике в наноразмерных структурах создаются области, где движение носителей ограничено в одном измерении, и можно считать, что эти носители находятся в одномерной потенциальной яме (например, электроны в нанометровом слое узкозонного материала между двумя слоями широкозонного).