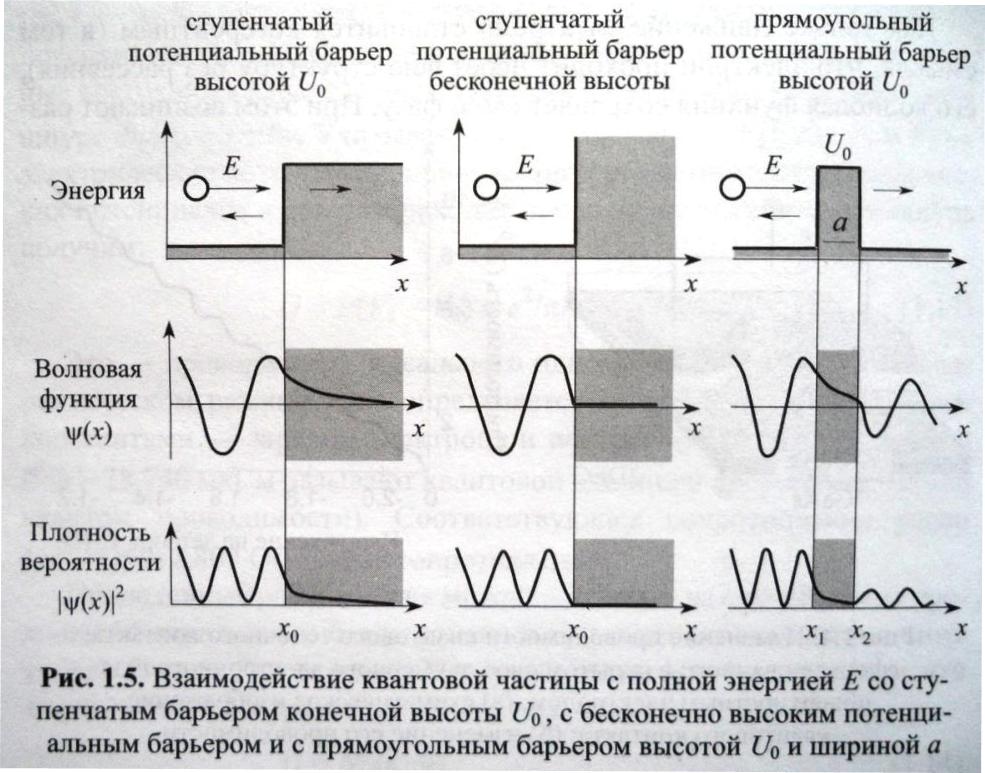
Туннельный эффект.

Если высота потенциального барьера конечна (U⁰), то амплитуда волновой функции при x = 0 и x = L не обращается в нуль и имеет продолжение внутри барьера. В этом случае частица может проникать внутрь барьера при энергиях E < U⁰, что противоречит закону сохранения энергии и не наблюдается в макромире. Если ширина барьера не бесконечна, то имеется отличная от нуля вероятность проникновения частицы за пределы барьера – туннельный эффект. Т.эффект лежит в основе действия многих схемных элементов наноэлектроники.

Квантовое ограничение. Простейшие виды низкоразмерных объектов.

В низкоразмерной структуре свободное движение электрона ограничено по крайней мере в одном направлении. В данном направлении электрон находится в потенциальной яме.

Ограничение движения электронов (дырок) в низкоразмерной структуре, приводящее (вследствие их квантово-волновой природы) к ненулевому минимальному значению их энергии и дискретности разрешенных состояний, называют квантовым ограничением ( quantum confinement).

В твердых телах КО может быть реализовано в трех пространственных направлениях. Количество направлений, в которых эффект квантового ограничения отсутствует, используется в качестве критерия для классификации элементарных низкоразмерных структур по трем группам:

• квантовые пленки (ямы) (2D),

• квантовые шнуры (нити, проволоки) (1D),

• квантовые точки (0D).

Можно сказать по-другому: в основе классификации лежит наличие квантоворазмерных эффектов, к которым, в частности, относится КО.

Квантовые размерные эффекты (в электронных структурах) имеют место тогда, когда протяженность тела, по крайней мере в одном направлении, становится сравнимой с квантовой характеристикой – длиной волны де Бройля для электронов. Квантоворазмерные эффекты обусловлены волновой природой электронов. Примеры КЭ в наноструктурах: квантование энергии электронов, прохождение электронов сквозь нанометровые диэлектрические слои, квантование сопротивления нанопроволок.Длина волны де Бройля для электрона в кристалле .Для свободных электронов в металле:

E_kin  5эВ, m^*  m₀ = 9.110^-31 кг.

  0.55 нм.

В полупроводниках:

E_kin  kT = 0.026 эВ (T = 300 K).

Кремний: m^* = 0.92m₀ и   8 нм.

GaAs: m^* = 0.068m₀ и   30 нм.

 электрона в полупроводнике больше, чем в металле, следовательно, квантоворазмерные эффекты технологически легче осуществить на полупроводниках.

Простейшие виды низкоразмерных объектов

КВАНТОВАЯ ЯМА

Квантовая яма – двумерный (2D) объект. Это тонкий слой кристалла, толщина которого d соизмерима с длиной волны де Бройля.

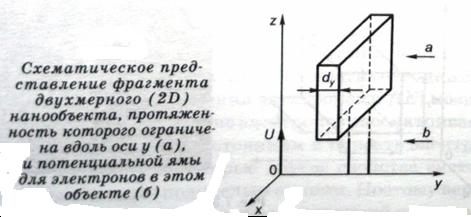
Движение электронов в этом слое ограничено отрезком d_y в направлении y и не ограничено в направлениях x и z. Двигаясь в направлении y, электрон не способен покинуть слой, так как его работа выхода (4.5 эВ) много больше энергии теплового движения (0.026 эВ при Т = 300К). Примечание: здесь и далее речь идет о п/п материалах. Поэтому движение в направлении y можно рассматривать как движение в одномерной бесконечно глубокой потенциальной яме шириной d_y.

Примером квантовых ям с 2D-электронным газом могут служить проводящие каналы в униполярных транзисторах (МОП-структуры на кремнии) и узкозонные слои в гетероструктурах для инжекционных лазеров.

Системы близкорасположенных параллельных квантовых ям, между которыми возможно туннелирование электронов, составляют сверхрешетки.

КВАНТОВАЯ НИТЬ

Квантовая нить (проволока) – одномерный (1D) объект.

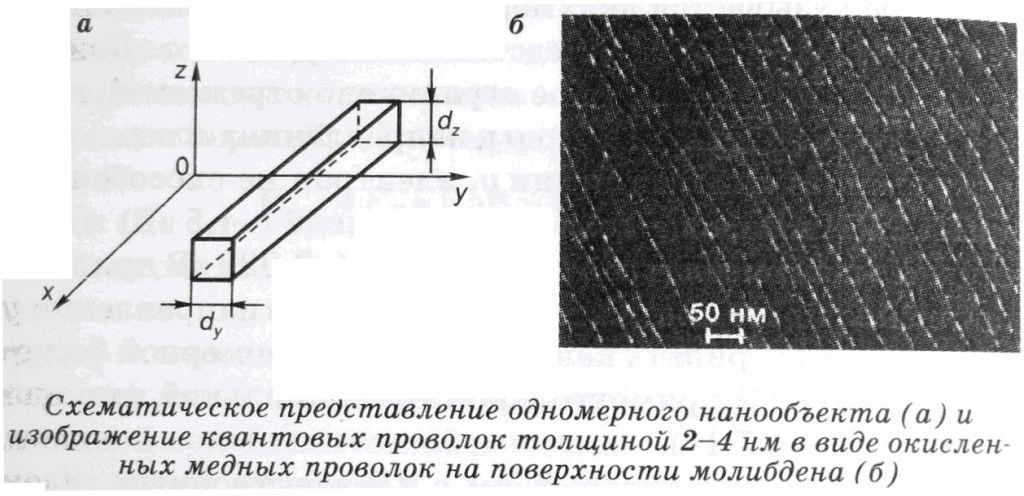
Движение электронов ограничено вдоль осей y и z размерами d_y и d_z соответственно и не ограничено вдоль оси x. Сечение квантовой проволоки может быть и иным, чем это изображено на рисунке. Потенциальная яма для свободных электронов в нити двухмерна.

КВАНТОВАЯ ТОЧКА

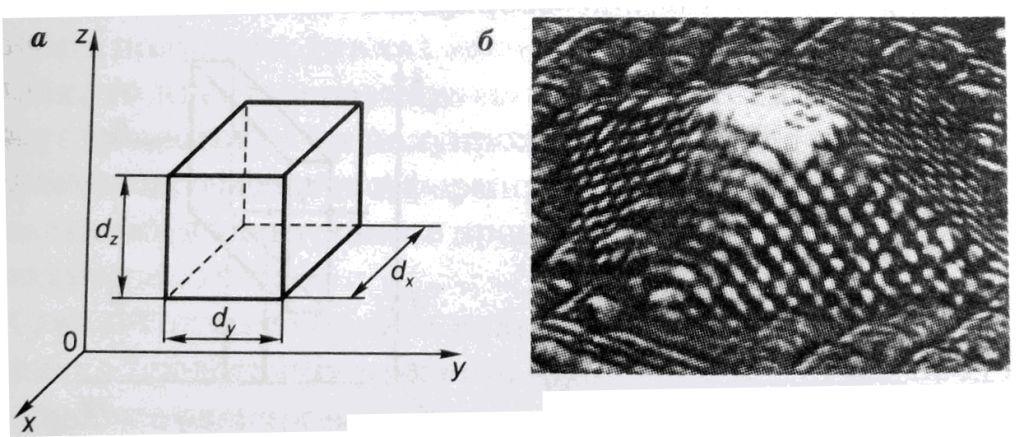
Квантовая точка – нульмерный (0D) объект.

Схематическое представление нульмерного нанообъекта (а) и изображение германиевой квантовой точки на поверхности кремния, полученное с помощью сканирующего туннельного микроскопа (б). Сторона основания пирамиды  10 нм, высота – 1.5 нм.

Движение электронов ограничено в трех измерениях. Пример – нанокристаллики одного материала на поверхности растущего эпитаксиального слоя другого материала. Потенциальная яма для квантовой точки трехмерна.