Физические основы наноэлектроники
Поведение электронов и дырок в наноструктурах определяют три группы фундаментальных явлений:
квантовое ограничение;
баллистический транспорт и квантовая интерференция;
туннелирование носителей заряда.
Все эти эффекты являются типичными квантово-механическими явлениями.
Квантовое ограничение возникает, когда свободное движение электронов в каком-либо направлении ограничено потенциальными барьерами. Оно изменяет спектр энергетических состояний и влияет на перенос носителей зарядов через наноструктуры.
Транспорт носителей заряда может осуществляться как параллельно, так и перпендикулярно потенциальным барьерам. В случае движения носителей вдоль потенциальных барьеров доминирующими эффектами оказываются баллистический транспорт и квантовая интерференция. Прохождение носителей заряда через потенциальные барьеры имеет место посредством их туннелирования.
Начальные элементы квантовой механики
См. записи лекции с описанием эксперимента по интерференции электронов. В литературе: фейнмановские лекции, 3-4 том.
Исходные принципы квантовой механики:
1. Вероятность
события в идеальном опыте дается
квадратом абсолютной величины комплексного
числа , называемого
амплитудой вероятности. Т.о., P
=
.
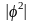2. Если событие
может произойти несколькими взаимно
исключающими способами, то амплитуда
вероятности события – это сумма амплитуд
вероятностей каждого отдельного способа.
Возникает интерференция:
= 1
+ 2
, P
=
.
3. Если ставится опыт, позволяющий узнать какой из этих взаимно исключающих способов осуществляется, то вероятность события – это сумма вероятностей каждого отдельного способа. Интерференция отсутствует. P = P1 + P2.
Общая формулировка принципа неопределенности: нельзя создать прибор, определяющий, какое из двух взаимно исключающих событий осуществилось без того, чтобы в то же время не разрушилась интерференционная картина.
Принцип неопределенности в формулировке Гейзенберга: при определении x-компоненты импульса тела с неопределенностью px, нельзя одновременно определить координату x тела с точностью, большей, чем x = h/p.
Волновая функция. Уравнение Шредингера
С любой частицей ассоциируется волновое поле, амплитуда которого задается функцией Ψ(x,t), известной как волновая функция.
Волновая
функция имеет вероятностную интерпретацию
и квадрат ее модуля
пропорционален
вероятности (на единицу длины) нахождения
частицы в данной точке пространства в
данный момент времени.
.
.
Нормировка:
Если волновая функция зависит от местоположения и времени, то используется зависящее от времени уравнение Шредингера:
.
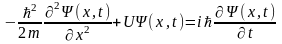Если рассматривается стационарное состояние, в котором Ψ и U не являются функциями времени, то приходим к стационарному виду уравнения Шредингера:
.
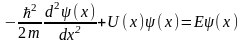E
=
–
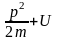полная энергия.
H
=
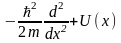- оператор Гамильтона.
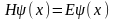- стационарное уравнение Шредингера.
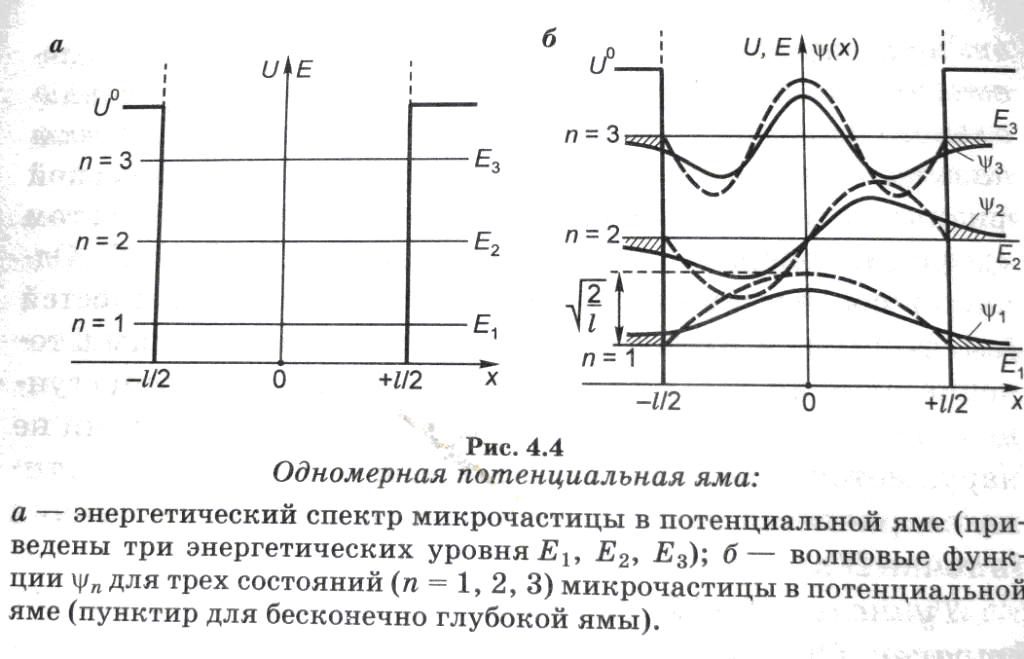
Частица в прямоугольной потенциальной яме
Тело, подчиняющееся законам классической физики, при движении в потенциальной яме имеет непрерывный энергетический спектр, то есть эго энергия E изменяется непрерывным образом.
Энергетический спектр частицы в наноразмерной потенциальной яме дискретен. Этот квантовый эффект лежит в основе функционирования многих наноэлектронных структур.
Поведение частицы в потенциальной яме строго описывается с помощью уравнения Шредингера. Должна быть задана потенциальная энергия U(x, y, z).
Рассмотрим одномерный случай (U зависит только от x) и яму простейшей прямоугольной формы.
U = 0, 0 < x < L,
U = , (x) = 0 x 0, x L.
.
Так как неизвестно, где точно находится частица внутри ямы в каждый момент времени, нельзя использовать величины, зависящие от времени. Применяем стационарное уравнение Шредингера:
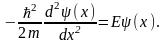
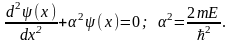
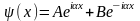- это суперпозиция двух волн в яме,
которые распространяются в противоположных
направлениях вдоль оси x.
Волновая функция представлена в
виде стоячих волн.
Для определения A и B используем граничные условия:
x = 0: (x) = 0, сл-но A + B = 0 и A = -B.
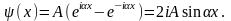
x
= L: (x)
= 0, сл-но
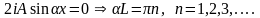
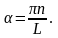
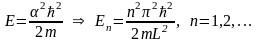
Энергия квантуется на дискретные значения.
Частица не может иметь энергию, равную нулю, что противоречит классической механике.
,
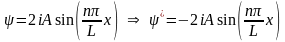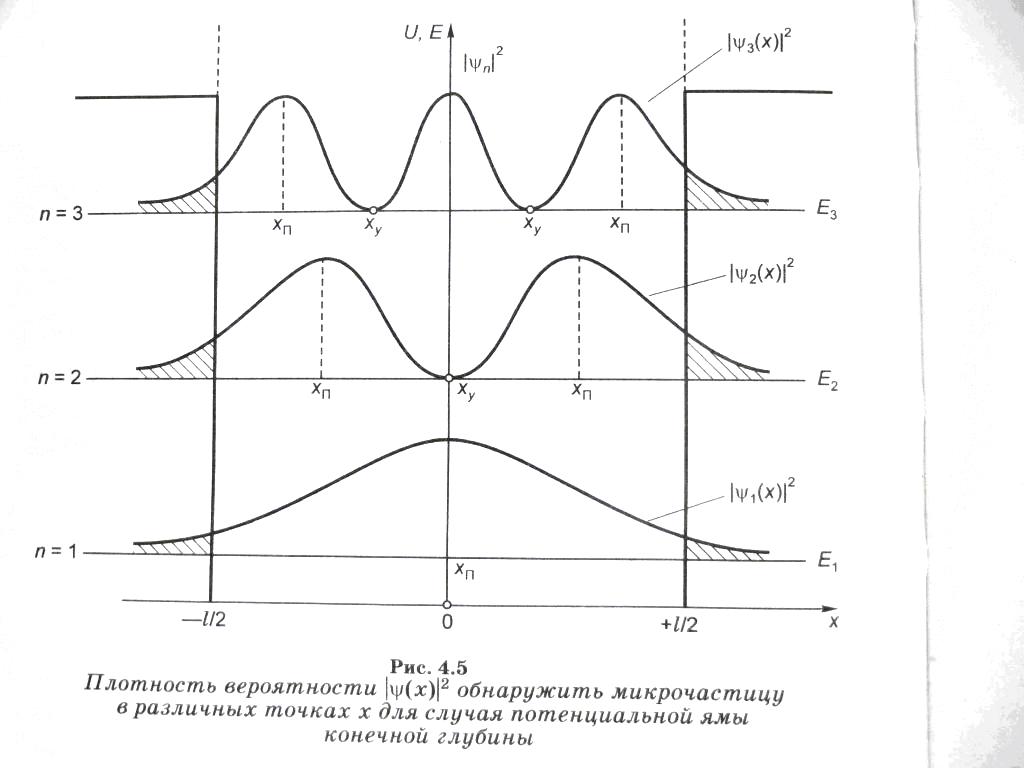
и плотность вероятности
.
Значение A находим из условия нормирования:
.
.
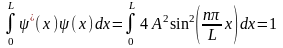