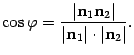- •1.Определение системы координат на прямой линии, и прямоугольных систем координат на плоскости и в пространстве.
- •2. Определение полярных координат на плоскости - . Связь полярных координат с координатами в прямоугольной системе координат.
- •4. Геометрический смысл и физический смысл линейных операций с векторами: сумма векторов , и умножение вектора на вещественное число .
- •Разностью a – b вектора a и вектор b называется такой вектор с, который в сумме с вектором b дает вектор a. (стр. 48 Аналитической Геометрии)
- •6. Операции над векторами
- •7.Определение линейной зависимости совокупности векторов , ,…, : привести два определения и показать их равносильность.
- •8.Определение базиса для векторов,расположенных на плоскости и в пространстве.Что значит базис ортогональный?
- •9.Определение,физический смысл и основные свойства скалярного произведения векторов а и b.Вычисление скалярного произведения.
- •10.Заданы векторы а и b.Как вычислить проекцию вектора а на направление определяемое вектором b?
- •11.Заданы векторы а и b.Как вычислить угол между a и b?
- •12.Определение,физический смысл и основные свойства векторного произведения векторов:a и b
- •13.Определение и основные свойства векторов a b c.Геометрический смысл смешанного произведения. Вычисление смешанного произведения векторов.
- •16. Вывод уравнения прямой на плоскости «в отрезках».
- •18.Нормирование общего уравнения прямой линии : . Получение выражения для вычисления отклонения произвольной точки от заданной прямой линии .
- •19. Вычисление расстояния от точки до прямой линии : .
- •20. Вычисление угла между двумя прямыми : и : .
- •22. Вывод уравнения плоскости, определяемой тремя точками: , , , не принадлежащими одной прямой.
- •23. Уравнение плоскости в отрезках.
- •24. Общее уравнение (полное) плоскости
- •25. Расстояние от точки , до плоскости, заданной уравнением , вычисляется по формуле:
- •26. Угол между плоскостями
- •27. Параметрическое уравнение прямой
- •Каноническое уравнение прямой
- •28. Уравнение прямой в пространстве, проходящей через две точки.
- •30. Угол между прямой и плоскостью.
- •Вопрос 31.
- •Вопрос 32.
- •Вопрос 33.
23. Уравнение плоскости в отрезках.
Если
в общем уравнении Ах + Ву + Сz
+ D
= 0 поделить обе части на -D
![]() ,
заменив
,
заменив
![]() ,
получим уравнение плоскости в отрезках:
,
получим уравнение плоскости в отрезках:
![]() Числа
a,
b,
c
являются точками пересечения плоскости
соответственно с осями х, у, z.
Числа
a,
b,
c
являются точками пересечения плоскости
соответственно с осями х, у, z.
24. Общее уравнение (полное) плоскости
![]()
где
![]() и
и
![]() —
постоянные, причём
—
постоянные, причём
![]() и
и
![]() одновременно
не равны нулю; в векторной
форме:
одновременно
не равны нулю; в векторной
форме:
![]()
где
![]() —
радиус-вектор точки
—
радиус-вектор точки
![]() ,
вектор
,
вектор
![]() перпендикулярен
к плоскости (нормальный вектор).
Направляющие
косинусы
вектора
перпендикулярен
к плоскости (нормальный вектор).
Направляющие
косинусы
вектора
![]() :
:
![]()
![]()
![]()
Нормальное (нормированное) уравнение плоскости
![]()
в векторной форме:
![]()
где
![]() -
единичный вектор,
-
единичный вектор,
![]() —
расстояние П. от начала координат.
Уравнение (2) может быть получено из
уравнения (1) умножением на нормирующий
множитель
—
расстояние П. от начала координат.
Уравнение (2) может быть получено из
уравнения (1) умножением на нормирующий
множитель
![]()
(знаки
![]() и
противоположны).
и
противоположны).
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Отклонение точки
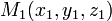 от
плоскости заданной нормированным
уравнением
от
плоскости заданной нормированным
уравнением
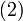
![]()
![]() ,если
,если
![]() и
начало координат лежат по разные стороны
плоскости, в противоположном случае
и
начало координат лежат по разные стороны
плоскости, в противоположном случае
![]() .
Расстояние от точки до плоскости равно
.
Расстояние от точки до плоскости равно
![]()
25. Расстояние от точки , до плоскости, заданной уравнением , вычисляется по формуле:
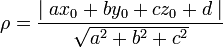
26. Угол между плоскостями
Пусть
плоскости
![]() и
и
![]() заданы
соответственно уравнениями
заданы
соответственно уравнениями
![]() и
и
![]() .
Требуется найти угол
.
Требуется найти угол
![]() между
этими плоскостями.
между
этими плоскостями.
Плоскости,
пересекаясь, образуют четыре двугранных
угла (рис. 11.6): два тупых и два острых или
четыре прямых, причем оба тупых угла
равны между собой, и оба острых тоже
равны между собой. Мы всегда будем искать
острый угол. Для определения его величины
возьмем точку
![]() на
линии пересечения плоскостей и в этой
точке в каждой из плоскостей проведем
перпендикуляры
на
линии пересечения плоскостей и в этой
точке в каждой из плоскостей проведем
перпендикуляры
![]() и
и
![]() к
линии пересечения. Нарисуем также
нормальные векторы
к
линии пересечения. Нарисуем также
нормальные векторы
![]() и
и
![]() плоскостей
и
с
началами в точке
(рис.
11.6).
плоскостей
и
с
началами в точке
(рис.
11.6).

Рис.11.6.Угол между плоскостями
Если
через точку
провести
плоскость
![]() ,
перпендикулярную линии пересечения
плоскостей
и
,
то прямые
и
и
изображения векторов
и
будут
лежать в этой плоскости. Сделаем чертеж
в плоскости
(возможны
два варианта: рис. 11.7 и 11.8).
,
перпендикулярную линии пересечения
плоскостей
и
,
то прямые
и
и
изображения векторов
и
будут
лежать в этой плоскости. Сделаем чертеж
в плоскости
(возможны
два варианта: рис. 11.7 и 11.8).

Рис.11.7.Угол между нормальными векторами острый

Рис.11.8.Угол между нормальными векторами тупой
В
одном варианте (рис. 11.7)
![]() и
и
![]() ,
следовательно, угол
,
следовательно, угол
![]() между
нормальными векторами равен углу
,
являющемуся линейным углом острого
двугранного угла между плоскостями
и
.
между
нормальными векторами равен углу
,
являющемуся линейным углом острого
двугранного угла между плоскостями
и
.
Во
втором варианте (рис. 11.8)
![]() ,
а угол
между
нормальными векторами равен
,
а угол
между
нормальными векторами равен
![]() .
Так как
.
Так как
![]() то в обоих случаях
то в обоих случаях
![]() .
.
По
определению скалярного произведения
![]() .
Откуда
.
Откуда
![]()
и соответственно
|
(11.4) |
Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула (11.4) позволяет найти косинус острого угла между плоскостями.
Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей:
|
(11.5) |
Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей
|
(11.6) |
где
![]() --
любое число.
--
любое число.