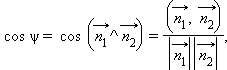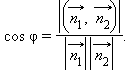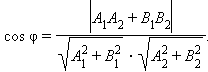- •1.Определение системы координат на прямой линии, и прямоугольных систем координат на плоскости и в пространстве.
- •2. Определение полярных координат на плоскости - . Связь полярных координат с координатами в прямоугольной системе координат.
- •4. Геометрический смысл и физический смысл линейных операций с векторами: сумма векторов , и умножение вектора на вещественное число .
- •Разностью a – b вектора a и вектор b называется такой вектор с, который в сумме с вектором b дает вектор a. (стр. 48 Аналитической Геометрии)
- •6. Операции над векторами
- •7.Определение линейной зависимости совокупности векторов , ,…, : привести два определения и показать их равносильность.
- •8.Определение базиса для векторов,расположенных на плоскости и в пространстве.Что значит базис ортогональный?
- •9.Определение,физический смысл и основные свойства скалярного произведения векторов а и b.Вычисление скалярного произведения.
- •10.Заданы векторы а и b.Как вычислить проекцию вектора а на направление определяемое вектором b?
- •11.Заданы векторы а и b.Как вычислить угол между a и b?
- •12.Определение,физический смысл и основные свойства векторного произведения векторов:a и b
- •13.Определение и основные свойства векторов a b c.Геометрический смысл смешанного произведения. Вычисление смешанного произведения векторов.
- •16. Вывод уравнения прямой на плоскости «в отрезках».
- •18.Нормирование общего уравнения прямой линии : . Получение выражения для вычисления отклонения произвольной точки от заданной прямой линии .
- •19. Вычисление расстояния от точки до прямой линии : .
- •20. Вычисление угла между двумя прямыми : и : .
- •22. Вывод уравнения плоскости, определяемой тремя точками: , , , не принадлежащими одной прямой.
- •23. Уравнение плоскости в отрезках.
- •24. Общее уравнение (полное) плоскости
- •25. Расстояние от точки , до плоскости, заданной уравнением , вычисляется по формуле:
- •26. Угол между плоскостями
- •27. Параметрическое уравнение прямой
- •Каноническое уравнение прямой
- •28. Уравнение прямой в пространстве, проходящей через две точки.
- •30. Угол между прямой и плоскостью.
- •Вопрос 31.
- •Вопрос 32.
- •Вопрос 33.
20. Вычисление угла между двумя прямыми : и : .
1. Если прямые L1 и L2 заданы общими уравнениями
А1х + В1у + С1 = 0 и А2х + В2у + С2 = 0,
то угол между ними равен углу между их нормалями, то есть между векторами {A1,B1} и {A2,B2}.
Обозначим
через φ величину угла между
прямыми ![]() и
и ![]() (напомним,
что угол между прямыми измеряется от
0° до 90°), а через ψ – угол между нормальными
векторами
(напомним,
что угол между прямыми измеряется от
0° до 90°), а через ψ – угол между нормальными
векторами 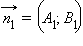 и
и 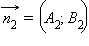 этих
прямых. Если ψ ≤ 90°,
то φ = ψ.
Если же ψ > 90°,
то φ = 180° – ψ.
В обоих случаях верно равенство
этих
прямых. Если ψ ≤ 90°,
то φ = ψ.
Если же ψ > 90°,
то φ = 180° – ψ.
В обоих случаях верно равенство ![]() следует,
что
следует,
что
|
и, следовательно,
|
Записав через координаты, получим
|
21.
Вывод общего уравнения плоскости, если
задана точка
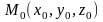 ,
принадлежащая этой плоскости, и вектор
нормали
=
,
принадлежащая этой плоскости, и вектор
нормали
=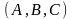 ,
перпендикулярный этой плоскости(M=M0)
,
перпендикулярный этой плоскости(M=M0)
Рассмотрим
произвольную точку ![]() в
пространстве и некоторый вектор
в
пространстве и некоторый вектор ![]() Очевидно,
что геометрическим местом точек
Очевидно,
что геометрическим местом точек ![]() таких,
что вектор
таких,
что вектор ![]() перпендикулярен
вектору
перпендикулярен
вектору ![]() будет
плоскость, проходящая через точку M
перпендикулярно
прямой, для которой вектор
будет
плоскость, проходящая через точку M
перпендикулярно
прямой, для которой вектор ![]() является
направляющим. Нашей задачей будет
установить уравнение плоскости, то есть
найти соотношение, которому удовлетворяют
координаты точки A.
является
направляющим. Нашей задачей будет
установить уравнение плоскости, то есть
найти соотношение, которому удовлетворяют
координаты точки A.
Запишем условие перпендикулярности векторов с использованием скалярного произведения:
|
Запишем последнее равенство в координатах:
|
Поскольку все наши выкладки были равносильными, то это и есть уравнение плоскости, проходящей через заданную точку. Преобразуем его к виду
|
Обозначая 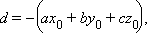 получим
получим
|
Это и есть так называемое общее уравнение плоскости.
22. Вывод уравнения плоскости, определяемой тремя точками: , , , не принадлежащими одной прямой.
Плоскость
может быть задана тремя точками, лишь
бы они не лежали на одной прямой, то есть
если они не коллинеарные. Получим
уравнение плоскости для трех заданных
точек. Для этого рассмотрим определение
векторного произведения. Результатом
векторного произведения двух
векторов ![]() является
вектор
является
вектор ![]() ,
модуль которого равен
,
модуль которого равен ![]() ,
и направлен он перпендикулярно плоскости
в которой лежат векторы
,
и направлен он перпендикулярно плоскости
в которой лежат векторы ![]() и
и ![]() ,
причем векторы
,
причем векторы ![]() – образуют
правую тройку векторов (см. определение
правой системы координат), здесь
– образуют
правую тройку векторов (см. определение
правой системы координат), здесь ![]() также
угол между векторами
и
.
Для векторов единичного базиса, образующих
правую тройку, как следует из
определения:
также
угол между векторами
и
.
Для векторов единичного базиса, образующих
правую тройку, как следует из
определения: ![]() ,
, ![]() ,
, ![]() .
Векторное произведение также подчиняется
дистрибутивному закону как и скалярное
произведение. Однако векторное
произведение не коммутативно, а именно,
если для векторов
.
Векторное произведение также подчиняется
дистрибутивному закону как и скалярное
произведение. Однако векторное
произведение не коммутативно, а именно,
если для векторов ![]() ,
то
,
то ![]() ,
что также прямо следует из определения.
Координаты векторного произведения
легко получить разложив векторы,
участвующие в произведении, по базису,
а затем раскрыв скобки, подобно тому
как это уже было проделано для скалярного
произведения. Есть и другой, неформальный,
но легче запоминаемый способ получения
координат векторного произведения, с
помощью разложения следующего определителя
по его первой строке. Если
,
что также прямо следует из определения.
Координаты векторного произведения
легко получить разложив векторы,
участвующие в произведении, по базису,
а затем раскрыв скобки, подобно тому
как это уже было проделано для скалярного
произведения. Есть и другой, неформальный,
но легче запоминаемый способ получения
координат векторного произведения, с
помощью разложения следующего определителя
по его первой строке. Если ![]() и
и ![]() ,
тогда
,
тогда
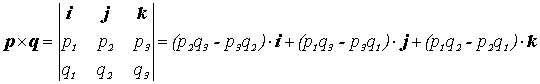
Сведем
теперь условия в новой постановке задачи
нахождения уравнения плоскости к
предыдущему случаю, где мы использовали
вектор нормали. Пусть заданы фиксированные
векторы ![]() и
,
не лежащие на одной прямой, определяющие
плоскость, уравнение которой требуется
получить (рис. 6).
и
,
не лежащие на одной прямой, определяющие
плоскость, уравнение которой требуется
получить (рис. 6).
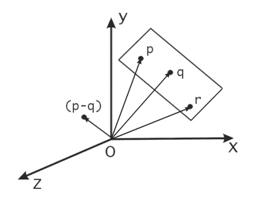
Рис. 6. Вывод уравнения плоскости проходящей через три точки.
Результат
векторного произведения любых двух
неколлинеарных векторов, параллельных
нашей плоскости, будет вектором
перпендикулярным плоскости. И как раз
такими являются векторы разности ![]() и
и ![]() .
Выберем их векторное произведение в
качестве вектора нормали, то есть
.
Выберем их векторное произведение в
качестве вектора нормали, то есть ![]() .
Тогда, если
.
Тогда, если ![]() –
произвольный радиус-вектор, принадлежащий
плоскости, то искомым уравнением
плоскости будет, аналогично формуле
(4):
–
произвольный радиус-вектор, принадлежащий
плоскости, то искомым уравнением
плоскости будет, аналогично формуле
(4):
![]() ,
,
причем в последней скобке вместо вектора можно было использовать, например, векторы или . Не будем далее расписывать это уравнение через координаты, так как это не трудно проделать самостоятельно.