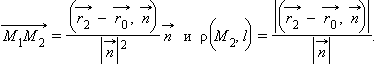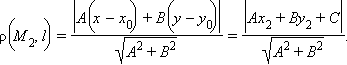- •1.Матрица. Линейные операции над матрицами. Действия над матрицами.
- •2.Определитель 2 –го и n-го порядков. Минор и алгебраическое дополнение.
- •3.Системы линейных уравнений. Метод Крамера.
- •4.Системы линейных уравнений Метод матричный.
- •5.Системы линейных уравнений Метод Гаусса.
- •6.Векторы, операции над векторами. Скалярное произведение векторов и его свойства.
- •7.Векторы, операции над векторами. Векторное произведение векторов и его свойства.
- •8.Орт вектора. Коллинеарность и ортогональность векторов.
- •9.Смешанное произведение векторов. Условие компланарности векторов.
- •10.Прямая на плоскости: общее уравнение; уравнение в отрезках; уравнение с угловым коэффициентом; уравнение прямой, проходящей через две данные точки.
- •11 Нормальное уравнение прямой. Расстояние от точки до прямой
- •12 Вычисление угла между прямыми
- •16.Вычисление угла между плоскостями.
- •17.Условия параллельности и перпендикулярности плоскостей.
- •18.Прямая в пространстве: общие, параметрические и канонические уравнения, их эквивалентность; уравнения прямой, проходящей через две данные точки.
- •19.Плоскость и прямая в пространстве. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости. Пересечение прямой и плоскости.
- •20 Кривые второго порядка
- •21 Основные элементарные функции и их свойства.
- •22.Понятие функции. Область определения и множество значений функции. Нечетность, периодичность.
- •23.Определение предела функции. Бесконечно малые и бесконечно большие функции.
- •24.Основные свойства бесконечно малых величин.
- •25.Теорема о связи бесконечно малых и бесконечно больших величин.
- •26.Первый замечательный предел.
- •27.Второй замечательный предел.
- •28.Непрерывность функции.
11 Нормальное уравнение прямой. Расстояние от точки до прямой
Пусть на плоскости хОу дана прямая. Проведем через начало координат перпендикуляр к данной прямой и назовем его нормалью. Обозначим через Р точку пересечения нормали с данной прямой и установим положительное направление нормали от точки О к точке Р.
Если
![]() -
полярный угол нормали, р - длина отрезка
-
полярный угол нормали, р - длина отрезка
![]() (рис.),
то уравнение данной прямой может быть
записано в виде
(рис.),
то уравнение данной прямой может быть
записано в виде
уравнение
этого вида называется нормальным.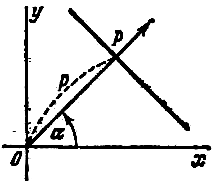
Пусть
дана какая-нибудь прямая и произвольная
точка
![]() ;
обозначим через d
расстояние от точки М* до данной прямой.
Отклонением
;
обозначим через d
расстояние от точки М* до данной прямой.
Отклонением
![]() точки
от
прямой называется число +d,
если данная точка и начало координат
лежат по разные стороны от данной прямой,
и -d,
если данная точка и начало координат
расположены по одну сторону от данной
прямой. (Для точек, лежащих на самой
прямой,
=0).
Если даны координаты
точки
от
прямой называется число +d,
если данная точка и начало координат
лежат по разные стороны от данной прямой,
и -d,
если данная точка и начало координат
расположены по одну сторону от данной
прямой. (Для точек, лежащих на самой
прямой,
=0).
Если даны координаты
![]() ,
,
![]() точки
и
нормальное уравнение прямой
точки
и
нормальное уравнение прямой
![]() ,
то отклонение
точки
от
этой прямой может быть вычислено по
формуле
,
то отклонение
точки
от
этой прямой может быть вычислено по
формуле
![]() .
.
Таким образом, чтобы найти отклонение какой-нибудь точки от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки . Полученное число будет равно искомому отклонению.
Чтобы
найти расстояние d
от точки до прямой, достаточно вычислить
отклонение и взять его модуль:
![]() .
.
Если
дано общее уравнение прямой
![]() ,
то, чтобы привести его к нормальному
виду, нужно все члены этого уравнения
умножить на нормирующий множитель
,
то, чтобы привести его к нормальному
виду, нужно все члены этого уравнения
умножить на нормирующий множитель
![]() ,
определяемый формулой
,
определяемый формулой
![]() .
.
Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.
12 Вычисление угла между прямыми
Пусть
прямые
![]() и
и
![]() заданы
общими уравнениями
заданы
общими уравнениями
|
Обозначим
через φ величину угла между прямыми
и
(напомним,
что угол между прямыми измеряется от
0° до 90°), а через ψ – угол между нормальными
векторами
![]() и
и
![]() этих
прямых. Если ψ ≤ 90°, то φ = ψ.
Если же ψ > 90°, то φ = 180° – ψ.
В обоих случаях верно равенство
этих
прямых. Если ψ ≤ 90°, то φ = ψ.
Если же ψ > 90°, то φ = 180° – ψ.
В обоих случаях верно равенство
![]() Из
теоремы
11.10
следует, что
Из
теоремы
11.10
следует, что
|
и, следовательно,
|
Записав через координаты, получим
|
Если
прямые
и
заданы
уравнениями с угловыми коэффициентами
![]() и
и
![]()
|
то
нормальные векторы этих прямых могут
быть
![]()
![]() и
выражение для косинуса угла между этими
прямыми будет иметь вид:
и
выражение для косинуса угла между этими
прямыми будет иметь вид:
|
Из
последнего выражения следует, что если
![]() то
cos φ = 1 и φ = 0, то есть прямые
параллельны или совпадают. С другой
стороны, если прямые параллельны, то
φ = 0 или cos φ = 1. Подставляя
в правую часть вместо cos φ его значение
1, умножая обе части на знаменатель и
возводя в квадрат, получим
то
cos φ = 1 и φ = 0, то есть прямые
параллельны или совпадают. С другой
стороны, если прямые параллельны, то
φ = 0 или cos φ = 1. Подставляя
в правую часть вместо cos φ его значение
1, умножая обе части на знаменатель и
возводя в квадрат, получим
|
Отсюда
получаем
![]()
Если
![]() то
cos φ = 0 и
то
cos φ = 0 и
![]() то
есть прямые перпендикулярны. Обратно,
если прямые перпендикулярны, то
то
есть прямые перпендикулярны. Обратно,
если прямые перпендикулярны, то
![]() или
cos φ = 0. Отсюда следует с
необходимостью
или
cos φ = 0. Отсюда следует с
необходимостью
![]()
Следовательно,
необходимые и достаточные условия
параллельности и перпендикулярности
двух прямых, заданных уравнениями с
угловыми коэффициентами
и
![]() формулируются
следующим образом.
формулируются
следующим образом.
Т![]() еорема 11.13.
еорема 11.13.
Для
того чтобы прямые
![]() и
и
![]() были
были
параллельны, необходимо и достаточно, чтобы
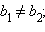
перпендикулярны, необходимо и достаточно, чтобы
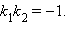
Пользуясь знанием координат направляющего и нормального векторов прямых, заданных общими уравнениями, можно сформулировать условия параллельности и перпендикулярности прямых через коэффициенты общих уравнений этих прямых.
Т еорема 11.14.
Для
того чтобы прямые
![]() и
и
![]() были
были
параллельны, необходимо и достаточно, чтобы соответствующие коэффициенты их уравнений при одноименных неизвестных были пропорциональны, то есть
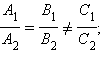
перпендикулярны, необходимо и достаточно, чтобы выполнялось равенство

Доказательство
|
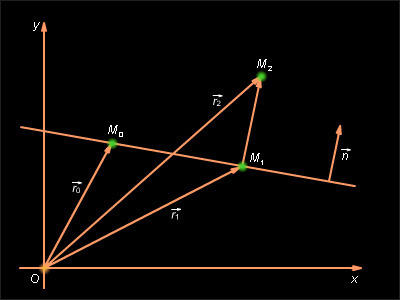
Пусть
задана прямая l
общим уравнением Ax + By + C = 0
и некоторая точка
![]() лежащая
вне прямой. Поставим задачу найти
расстояние
лежащая
вне прямой. Поставим задачу найти
расстояние
![]() от
этой точки до прямой l.
Опустим перпендикуляр
от
этой точки до прямой l.
Опустим перпендикуляр
![]() из
точки
из
точки
![]() на
прямую l
и обозначим
на
прямую l
и обозначим
![]()
![]() радиус-векторы
точек
радиус-векторы
точек
![]() и
соответственно
(см. рис. 11.6.1). Очевидно,
и
соответственно
(см. рис. 11.6.1). Очевидно,
![]()
1 |
Рисунок 11.6.1. |
Пусть
![]() –
некоторая точка прямой l,
отличная от точки
–
некоторая точка прямой l,
отличная от точки
![]() Тогда
уравнение прямой l
можно записать в нормальной векторной
форме:
Тогда
уравнение прямой l
можно записать в нормальной векторной
форме:
|
где
![]() а
а
![]() –
вектор нормали к прямой l.
Или, в векторной форме,
–
вектор нормали к прямой l.
Или, в векторной форме,
![]()
Очевидно,
справедливо векторное равенство
![]() причем
причем
![]() поэтому
поэтому
![]() Умножив
обе части равенства скалярно на вектор
Умножив
обе части равенства скалярно на вектор
![]() , получим
, получим
|
Так
как точка
лежит
на прямой l,
то
![]() и,
следовательно,
и,
следовательно,
![]() Подставляя
в исходное равенство, найдем
Подставляя
в исходное равенство, найдем
|
Отсюда
|
Переходя
к координатной форме записи и учитывая,
что
![]() имеем
имеем
|
Таким образом верна теорема
Т еорема 11.15.
Растояние
от
точки
![]() до
прямой l,
заданной уравнением Ax + By + C = 0
вычисляется по формуле
до
прямой l,
заданной уравнением Ax + By + C = 0
вычисляется по формуле
|
14.Плоскость в пространстве: общее уравнение; уравнение в отрезках; уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору; уравнение плоскости, проходящей через три данные точки.
Плоскость в пространстве.
Получим сначала уравнение плоскости, проходящей через точку М0(х0 ,у0 ,z0) перпендикулярно вектору n = {A,B,C},называемому нормалью к плоскости. Для любой точки плоскости М(х, у, z) вектор М0М = {x - x0 , y - y0 , z - z0) ортогонален вектору n, следовательно, их скалярное произведение равно нулю:
A(x - x0) + B(y - y0) + C(z - z0) = 0. (8.1)
Получено уравнение, которому удовлетворяет любая точка заданной плоскости – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
После приведения подобных можно записать уравнение (8.1) в виде:
Ax + By + Cz + D = 0, (8.2)
где D = -Ax0 - By0 - Cz0. Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.
Неполные уравнения плоскости.
Если хотя бы одно из чисел А, В, С, D равно нулю, уравнение (8.2) называют неполным.
Рассмотрим возможные виды неполных уравнений:
1) D = 0 – плоскость Ax + By + Cz = 0 проходит через начало координат.
2) А = 0 – n = {0,B,C}Ox, следовательно, плоскость By + Cz + D = 0 параллельна оси Ох.
3) В = 0 – плоскость Ax + Cz +D = 0 параллельна оси Оу.
4) С = 0 – плоскость Ax + By + D = 0 параллельна оси Оz.
5) А = В = 0 – плоскость Cz + D = 0 параллельна координатной плоскости Оху (так как она параллельна осям Ох и Оу).
6) А = С = 0 – плоскость Ву + D = 0 параллельна координатной плоскости Охz.
7) B = C = 0 – плоскость Ax + D = 0 параллельна координатной плоскости Оуz.
8) А = D = 0 – плоскость By + Cz = 0 проходит через ось Ох.
9) B = D = 0 – плоскость Ах + Сz = 0 проходит через ось Оу.
10) C = D = 0 - плоскость Ax + By = 0 проходит через ось Oz.
11) A = B = D = 0 – уравнение Сz = 0 задает координатную плоскость Оху.
12) A = C = D = 0 – получаем Ву = 0 – уравнение координатной плоскости Охz.
13) B = C = D = 0 – плоскость Ах = 0 является координатной плоскостью Оуz.
Если же общее уравнение плоскости является полным ( то есть ни один из коэффициентов не равен нулю), его можно привести к виду:

Угол между плоскостями. Условия параллельности и
перпендикулярности плоскостей.
Если две плоскости (α1 и α2) заданы общими уравнениями вида:
A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0,
то очевидно, что угол между ними равен углу между их нормалями, то есть между векторами n1={A1,B1,C1) и n2={A2,B2,C2). Из формулы (5.6) получаем, что косинус угла между плоскостями α1 и α2 равен
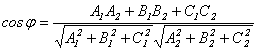 (8.4)
(8.4)
Условие параллельности плоскостей заключается в параллельности нормалей:
![]()
а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения:
A1A2 + B1B2 + C1C2 = 0.
Выведем еще несколько уравнений плоскости. Пусть плоскость проходит через точки М1(х1, у1, z1), M2(x2, y2, z2) и M3(x3, y3, z3), не лежащие на одной прямой. Тогда векторы М1М2={x2 - x1, y2 - y1, z2 - z1}, М1М3={x3 - x1, y3 - y1, z3 - z1} и М1М={x - x1, y - y1, z - z1}, где М(x, y, z) – произвольная точка плоскости, компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем:

Это уравнение, которому удовлетворяют координаты х, у, z любой точки, лежащей на искомой плоскости, является уравнением плоскости, проходящей через три данные точки.
Способом, аналогичным изложенному в лекции 7, можно получить нормальное уравнение плоскости:
![]() (8.8)
(8.8)
где р – длина перпендикуляра ОР, опущенного из начала координат на плоскость, а cosα, cosβ, cosγ – направляющие косинусы нормали к этой плоскости. При этом расстояние от любой точки А пространства до данной плоскости определяется по формуле:
![]() ,
(8.9)
,
(8.9)
где
x0,y0,z0 – координаты рассматриваемой
точки А. Подмодульное выражение в формуле
(8.9) называется отклонением точки А от
плоскости и принимает положительные
значения, если А и начало координат
лежат по разные стороны от плоскости,
и отрицательные, если эти две точки
лежат по одну сторону от плоскости.
Нормальное уравнение получается из
общего уравнения плоскости в результате
деления его на нормирующий множитель
![]() знак
которого противоположен знаку D.
знак
которого противоположен знаку D.


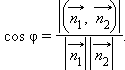
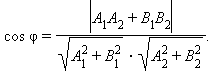
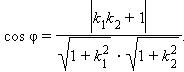

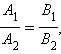

 то
прямые параллельны.
то
прямые параллельны.