6. Простой трубопровод. Расчет потерь напора в трубопроводе. Кривые потребного напора простого трубопровода.

6. П оследовательное и паралельное соед. простых трубопроводов. Построение результирующих линий потребного напора. Последовательное соединение простых: Такой трубопровод состоит из последовательно соединенных труб различных диаметров и длин, содержащих разнообразные местные сопротивления. Исходными положениями при расчете таких трубопроводов являются:1) расход текучей среды по длине трубопровода является постоянной величиной, т.е. V₁= V₂ = V₃ = V₄ = V_c; 2) разность напоров Н в начале трубопровода (сеч. 1 – 1) и в конце – (сеч. 4-й) расходуется на преодоление сопротивлений и равна сумме потерь напора на отдельных участках Принцип расчета трубопровода переменного сечения остается таким же, что и в случае трубопровода постоянного сечения. Однако при определении напора Н по уравнению (8.4) следует учитывать разность скоростных напоров в конце и начале трубопровода, т.е. В приведенном уравнении коэффициент Кориолиса для различных участков определяется по известному уравнению: где λ – коэффициент гидравлического трения. Более удобно сложный трубопровод рассчитать используя графо-аналитический метод. Суть этого метода состоит в том, что сложный трубопровод разбивается на участки, представляющие собой простые трубопроводы (участок I – l_1;d₁; II –l₂;d₂; III – l₃;d₃). Далее производится расчет этих участков и строятся их графические характеристики: . Результирующая характеристика всего трубопровода определяется путем графического сложения потерь напора на отдельных участках при одинаковых расходах, как это показано на рисунке. 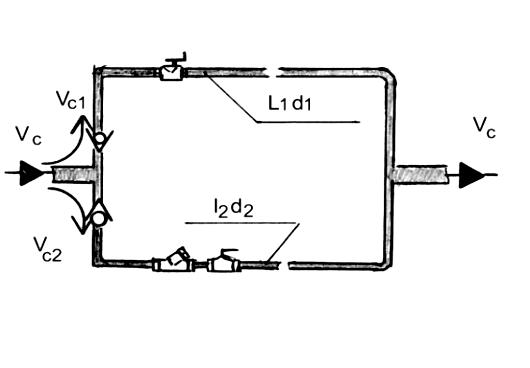Трубопровод с параллельными ветвями: Расчет такого трубопровода также целесообразно проводить графо-аналитическим методом с использованием графиков зависимости потерь напора от расхода составленных для каждой ветви сложного трубопровода (ветви трубопровода будут представлять собой простой трубопровод). Далее исходят из того, что сумма расходов в отдельных ветвях равна полному расходу (V_с= V_с1 + V_с2) и что потери во всех ветвях одинаковы (H=H₁=H₂). Зависимость полного напора H на разветвленном участке от расхода жидкости в ветвях V строится графическим сложением абсцисс кривых H₁ = f₁(V_с1) и H₂ = f₂ (V_с2).

7. Понятие гидравлического удара. Формула Журавского. Определение величины повышения давления при прямом полном и неполном гидравлическом ударе.

6. Истечение жидкости через отверстие в тонкой стенке при постоянном напоре.

К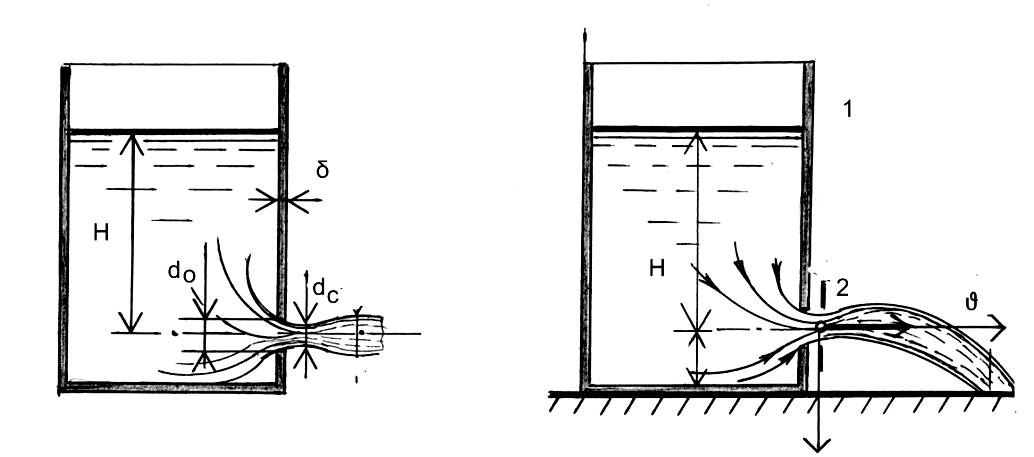 лассификация отверстий: Все отверстия, выполняемые в стенках либо днищах сосудов, классифицируют по форме: круглые, квадратные, овальные, прямоугольные и т.д.; по исполнению: в тонкой стенке, когда , где – толщина стенки, d – диаметр отверстия и в толстой стенке, когда . Кроме того, отверстия различают по размеру. Малыми отверстиями принято считать отверстия, у которых , где – напор перед отверстием; – разность напоров при затопленном отверстии. Для большинства отверстий справедливо соотношение или . При истечении жидкости из отверстия характерно то, что в процессе истечения запас потенциальной энергии, которым обладает жидкость в резервуаре, превращается, с большими или меньшими потерями, в кинетическую энергию струи и капель. Экспериментально установлено (см. рис.), что при истечении жидкости происходит сжатие струи от d₀ до d_c. Форма сжатой струи зависит от многих факторов, среди которых: форма и размер отверстия, толщина стенки, величина напора перед отверстием. Цилиндрическую форму струя принимает на расстоянии примерно равном одному диаметру отверстия, а сжатое сечение располагается на расстоянии равном половине диаметра отверстия. Сжатие струи происходит вследствие того, что частицы жидкости подходят к отверстию из всего прилегающего объема, двигаясь параллельными плавными траекториями. Входя в отверстие, частицы продолжают движение по инерции, траектории частиц сближаются, и размер сечения образовавшейся струи становится меньше сечения отверстия. Отношение площади сечения струи в месте наибольшего сжатия S_сж к площади отверстия S₀ называется степенью сжатия струи :

Истечение жидкости через отверстие в тонкой стенке при постоянном уровне: При вытекании жидкости через малое отверстие в стенке сосуда при постоянном уровне жидкости в нем движение жидкости в образовавшейся струе можно считать установившимся. Это позволяет в данном случае применить уравнение Л.Бернулли. Его запишем для двух сечений 1-1 и 2-2 (см. рис. 10.1,б). Сечение 1-1 проходит по свободной поверхности жидкости, на которую действует давление Сечение 2-2 располагаем по сжатому сечению струи, где скорость истечения . Струя вытекает в атмосферу соответственно р₂=р_а. При истечении через отверстие реальной жидкости ( ) уравнение Л.Бернулли для сечений 1-1 и 2-2 запишется в виде ,здесь – потери напора, связаные с преодолением сопротивления отверстия. – коэффициент сопротивления отверстия.. Имеем , тогда ; , поэтому ; поэтому значением пренебрегаем и, следовательно, скоростной напор . В данном случае уравнение (7.8) примет вид Откуда

Если сравнить уравнение (10.10) с уравнением (10.7), то нетрудно установить, что скорость истечения идеальной жидкости из отверстия в тонкой стенке будет выше, чем для реальной жидкости, на величину коэффициента скорости – Для малого отверстия коэффициент скорости . Откуда коэффициент сопротивления малого отверстия

При истечении из отверстия реальной жидкости ее расход определится по уравнению секундного расхода ,

где – коэффициент расхода, примерно равный 0,62. Численное значение коэффициентов определяются эксперементально. определяются непосредственным измерением действительного расхода и сечения струи по сравнению с их теоретическими величинами:

Ранее условились малыми отверстиями считать такое, вертикальный размер которого мал по сравнению с напором. Отверстия (люки, крышки, лазы), для которых это условие не выдерживается, считаются «большими» и расчет расхода жидкости для таких отверстий ведется по формуле ,где – напор, определенный до ценрта тяжести площади отверстия, м; F – площадь отверстия (люка, крышки, лаза), . Коэффициент расхода для больших отверстий зависит от формы отверстия; отношения вертикального размера d или a к среднему напору ; от коэффициента расхода отверстия . Он может быть определен по одному из двух нижеприведенных уравнений. Для круглого отверстия: , Для прямоугольного отверстия с высотой а: