6. Понятие местного сопротивления. Основные их виды. Расчет потерь напора на их преодоление. Эквивалентная длинна местных сопротивлений.

На практике все технологические трубопроводы собираются из отрезков труб одного или разных диаметров, соединенных между собой стандартными изделиями: угольниками (отводами), муфтами, тройниками, фланцами и т.д. В систему трубопроводной коммуникации включают запорно-регулирующие устройства: краны, задвижки, вентили, заслонки; измерительные устройства: диафрагмы, сопла, диффузоры. При движении по трубопроводу жидкость проходит через фильтры, клапана, дроссели. Каждое из перечисленных устройств вызывает изменение скорости либо по величине, либо по направлению, а чаще всего сразу и по величине, и по направлению. Как правило, при изменении скорости или направления потока происходит интенсивное вихреобразование и перемешивание потока, на что из потока расходуется энергия. Поэтому потоку необходимо больше затратить энергии при прохождении таких устройств (мест), чем при прохождении прямого участка. Т.к. эти потери энергии имеют сосредоточенный характер, их величина зависит от вида устройства, то условились называть ее местной потерей энергии (или напора) и подсчитывать по уравнению Дарси: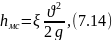 где ξ – коэффициент местного сопротивления. Он учитывает величину (долю от скоростного напора) теряемой энергии при прохождении потоком данного местного сопротивления. Величина коэффициента сопротивления определяется по справочникам, в зависимости от вида сопротивления, а иногда и режима движения. Однако часто для сохранения единообразия в расчетных формулах коэффициент ξ заменяется «эквивалентной длиной». Эквивалентной длиной называется такая длина прямого трубопровода гидравлическое сопротивление которого равно величине потерь напора на преодоление данного местного сопротивления. В соответствии с определением ; откуда

6. Внезапное расширение потока. Расчет потерь напора (уравнение Борда)

П ри внезапном расширении потока жидкость, обладающая инерцией, не может сразу заполнить трубу большего диаметра. Лишь пройдя некоторое расстояние от входа, поток заполняет все сечение трубы. Между торцевой стенкой устройства и большей стенкой трубы образуются вихревые зоны. В этих зонах жидкость, вовлекаемая в движение проходящим (транзитным) потоком постоянно перемещается по круговым траекториям, таким образом в зонах возникают вихри. Кроме этого, транзитный поток и вихри постоянно обмениваются частицами жидкости. На генерирование вихрей в отмеченных зонах, на заполнение их, на обмен частицами с основным потоком тратится его энергия. Эти затраты энергии называются потерями, связанными с преодолением внезапного расширения потока. Аналогично более простой или более сложный характер имеют потери в других местных сопротивлениях. Как привило, основную часть потерь при этом составляют потери, обусловленные сжатием потока и образованием вихревых зон. К ним в более или менее значительной степени добавляются потери, связанные с внутренним трением жидкости. В настоящее время строгому аналитическому расчету поддаются лишь некоторые виды сопротивлений, одним из которых является внезапное расширение. Впервые величину этих потерь и коэффициент сопротивления определил французский военный инженер Борд. Рассмотрим внезапное расширение трубы (рис.а). Будем полагать, что:1) ось потока горизонтальна z1=z2 ; 2)гидродинамическое давление распределяется по гидростатическому закону; 3) сила внешнего трения на границе раздела пренебрегают Т=0. Запишем уравнение Бернулли для сечений 1-1 и 2-2: откуда выразим величину потерь напора на преодоление данного вида местного сопротивления: Разность давлений определим, применив к объему жидкости, заключенному между сечениями 1-1 и 2-2, теорему об изменении количества движения в проекции на горизонтальную ось системы: Будем также считать, что коэффициент Кориолиса . Силами трения на пути между сечениями 1-1 и 2-2 пренебрегаем из-за близости расположения сечений. Вес жидкости и сила ее давления на стенки в пт роекции на ось потока будут равны нулю. Следовательно: Тогда уравнение перепишем в виде .Разделив полученное выражение на произведение , произведем необходимые преобразования левой части уравнения: и правой: Теперь в уравнение (7.18) подставим значение разности статических напоров , выражаемую из уравнений (7.22 и 7.23). В результате такой подстановки получим Приведя уравнение (7.24) к общему знаменателю, получим уравнение, называемое уравнением Борда: . Имея в виду, что , можем преобразовать уравнение (7.25) следующим образом: Эти преобразования привели к выводу о том, что для расчета потерь напора на преодоление местных сопротивлений возможно использовать уравнение Дарси (7.12), при этом коэффициент потерь при внезапном расширении потока равен В частном случае, когда поток выходит из трубы в бассейн , соотношение и коэффициент . В реальных трубопроводах местные сопротивления могут располагаться вблизи друг от друга. Ранее рассматриваемые по ходу потока местные сопротивления, возмущая поток, изменяют условия его течения через последующее местное сопротивление. Это взаимное влияние может оказывать как благоприятное воздействие на поток, уменьшая гидравлическое сопротивление участка, так и негативное – увеличивая его. В среднем, благоприятные влияния компенсируются неблагоприятными, и в гидравлике считают верным принцип наложения потерь, т.е. суммирование потерь на всех местных сопротивлениях, считая их отдельно расположенными и пренебрегая взаимным влиянием: или

6. Классификация трубопроводов. Расчет диаметра трубопровода. Понятие экономичной скорости. Как жидкости, так и газы перемещаются по системе труб, называемых трубопроводами либо воздухопроводами. В любом трубопроводе перемещение жидкости осуществляется благодаря тому, что ее энергия в начале трубопровода больше, чем энергия потока в конце трубопровода. Обычно энергия в поток вносится либо насосами при перемещении жидкостей, либо компрессорами при транспортировке газов. Кроме того, жидкостной поток может течь как за счет гидростатического давления (обусловленного разностью гидравлических высот расположения начального и конечного сечений потока), так и за счет избыточного давления газа 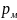в резервуаре, из которого забирается жидкость. Все трубопроводы делятся на простые и сложные: к простым относятся трубопроводы постоянного диаметра и не имеющие ответвлений. Сложные трубопроводы: 1) последовательно соедин. простые 2) паралельно соед. простые 3) разветвленные 4) замкнутые (кольцевые). Кроме того, трубопроводы делятся на короткие и длинные. Короткими считаются трубопроводы сравнительно небольшой длины ,в которых местные потери напора составляют не менее 5÷10% потерь напора по длине трубопровода, теряемых на трение. При их расчете исходят из принципа наложения потерь, принимая Длинные – это трубопроводы значительной протяженности, в которых потери на преодоления местных сопротивлений составляют не более 5÷10% от потерь напора по длине. При расчете таких трубопроводов потери на преодоление местных сопротивлений либо вовсе не учитывают, либо учитывают путем увеличения потерь напора по длине на 5÷10% т.е. Как следует из классификации трубопроводов, сложным является трубопровод, диаметр которого меняется по длине или имеются ответвления. Всякий сложный трубопровод можно представить как комбинацию простых, соединенных между собой различным образом. Принцип наложения потерь позволяет рассчитать потери напора в простом трубопроводе. Поэтому расчет сложных трубопроводов базируется на умении рассчитать простой трубопровод.