13. Расчет расхода жидкости при ламинарном режиме ( уравнение Пуазеля)

Определим расход жидкости, движущейся в ламинарном режиме по трубе круглого сечения диаметром D=2R. Для этого в потоке выделим элементарное кольцевое сечение с внутренним размером r и толщиной кольца dr (см. рис.). Площадь этого кольцевого сечения в направлении движения потока т.к. .

Объёмный расход через выделенное кольцевое сечение определяется как . Интегрируя полученное уравнение для всего потока, т.е. изменяя r от 0 по оси потока, до R у стенки трубы, получим

Уравнение является уравнением Пуазейля для определения расхода жидкости при ламинарном режиме движения.

6. Течение жидкости в малом зазоре. Уравнение Петрова.

6. Т урбулентный поток и его структура. Интенсивность пульсаций и турб. вязкость потока. Закон распределения скорости по сечению потока. В инженерной практике чаще встречается турбулентный режим движения жидкости. Поэтому этот режим движения достаточно трудно исследовать теоретически. Этот режим течения подвергается наиболее широким опытным исследованиям. При турбулентном режиме наблюдается интенсивное вихреобразование, частицы жидкости описывают сложные траектории движения, скорости меняются даже при постоянном расходе. Для турбулентного движения характерны три главных признака: большое разнообразие и быстрая изменяемость поля скоростей, хаотичность (неоднородность изменения скоростей в пространстве и во времени) и, наконец, интенсивное перемешивание жидкости. Эти особенности турбулентного движения заставляют считать его неустановившимся. Так, интенсивное перемешивание сопровождается появлением продольных и поперечных пульсаций скорости и давления. Вместе с тем, пульсации происходят около какого-то среднего значения (см. рис.): . Скорость в данной точке в любой момент времени (местная скорость) можно записать через осредненное значение: ,где 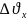, , – мгновенные пульсационные соответствующие скорости. Несмотря на кажущуюся беспорядочность изменения скоростей при турбулентном движении, значения осредненной скорости за достаточно большой промежуток времени остаются постоянными. Как и любое течение реальной жидкости, турбулентный поток по своей природе является диссипативным (т.е. в нем кинетическая энергия потока рассеивается и переходит в тепло). Если отсутствует непрерывный внешний источник энергии, необходимый для постоянного побуждения турбулентного движения, то это движение вырождается (затухает вследствие проявления вязкости среды). На рисунке представлена схема движения среды. 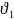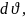Вследствие разности скоростей и , отличающихся на возникает касательное напряжение:

В случае ламинарного потока было бы существующим напряжением, возникающим между расположенными на расстоянии слоями жидкости. Однако в турбулентном потоке частицы жидкости перемещаются относительно друг друга не только в продольном, но и в поперечном направлении. Это создает дополнительные касательные напряжения , которые по аналогии с можно выразить . Величину называют турбулентной вязкостью. Она не является физико-химической константой. Определяется в зависимости от скорости и других параметров, обуславливающих степень турбулентности потока. Тогда касательное напряжение, возникающее в турбулентном потоке, выражается как . Структуру турбулентного потока условно делят на центральную зону, или основную массу жидкости, называемую ядром потока, в которой движение является развитым турбулентным, и гидродинамический пограничный слой вблизи стенки, где переходит турбулентное движение в ламинарное. Внутри этого слоя имеется ламинарный подслой толщиной , где превалирующее значение оказывают силы вязкости. Поэтому характер течения в подслое ламинарный. Ламинарный подслой имеет малую толщину (иногда сотые доли миллиметра), которая уменьшается с в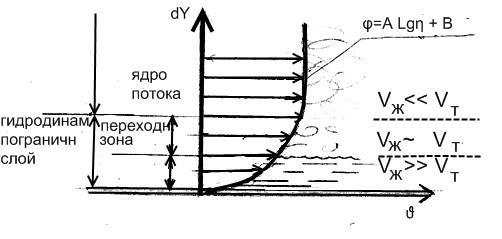 озрастанием степени турбулентности потока, что достигается увеличением скорости его движения. Толщина ламинарного подслоя вычисляется по уравнению Между ядром потока и ламинарным подслоем существует переходная зона. В совокупности ламинарный подслой и эту зону называют гидродинамическим пограничным слоем. Значения вязкости среды и турбулентной становятся сравнимыми по порядку. В пределах гидродинамического пограничного слоя скорость движения частиц резко меняется от нуля у стенки до среднего значения скорости в ядре потока. В ядре потока скорость остается постоянной. Эпюра скорости движения частиц при турбулентном режиме описывается логарифмическим законом распределения.

6. Г идравлические потери по длинне трубопровода. Вывод уранвения Дарси – Вейсбаха. Коэф. гидравлического трения. Величина потерь удельной энергии потока , входящая в уравнение Бернулли для потока реальной жидкости (уравнение 3.38), есть мера той механической энергии, которая благодаря работе сил трения равномерно по длине потока переходит в тепло и безвозвратно теряется потоком. Важность определения потерь напора (или потерь давления ) связана с необходимостью расчета затрат энергии, требуемых для компенсации этих потерь при перемещении подвижных сред, например, жидкостей и газов, с помощью насосов и вентиляторов. При движении идеальной жидкости касательные напряжения трения 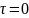и, следовательно, потери по длине отсутствуют. Потери напора в трубопроводе в общем случае обуславливаются сопротивлением трения и местными сопротивлениями. Сопротивления трения возникают при движении реальной жидкости по всей длине трубопровода. На их величину оказывает влияние режим течения жидкости и геометрические характеристики трубопровода. Местные сопротивления возникают при любых изменениях: либо скорости, либо направления движения потока, либо и то и другое, вместе взятое. Таким образом, Для ламинарного режима движения жидкости может быть найдено аналитически с применением уравнений Бернулли и Пуазейля. С этой целью на прямом участке трубопровода, приведенного на рис., выделим два сечения 1-1 и 2-2, расположенные друг от друга на расстоянии l. Для этих сечений запишем уравнением Бернулли, полученное для реальной жидкости: . Для горизонтального z₁=z₂, прямого трубопровода 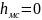, постоянного диаметра, или или уравнение Бернулли запишется в виде Откуда По уравнению Пуазейля (4.21) С другой стороны, расход жидкости через трубу диаметром d при средней скорости потока 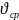составит После подстановки расхода жидкости в уравнение Пуазейля с учетом уравнения,получим выражение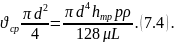 Или .

И числитель, и знаменатель правой части уравнения (7.5) домножим на величину 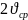. После домножения получим Таким образом, установлено, что потерянный напор (удельная энергия потока) затрачивается на компенсацию действия сил трения, выражается в долях от скоростного напора. Величину, равную называют коэффициентом гидравлического трения (коэффициентом Дарси). С учетом этого, уравнение может быть представлено в виде: . Полученное уравнение носит название уравнения Дарси–Вейсбаха для расчета потерь на трение в трубопроводе.

Учет режима течения осуществляется коэффициентом гидравлического трения λ

6. Г рафики И. Никурадзе. Абсолютная и относительная шераховатости труб . Понятие гидравлически гладких и шераховатых труб. Формулой Дарси–Вейсбаха пользуются при расчете гидравлических потерь в потоках, движущихся в трубах не только в ламинарном режиме. но и при любых других режимах течения. Учет режима течения осуществляется коэффициентом гидравлического трения λ. В 1933г. советский ученый И.Никурадзе обобщил собственные результаты, а также результаты ранее проведенных исследований другими учеными в виде графиков зависимости коэффициента гидравлического трения от режима течения и состояния стенок труб и каналов (см. рис.).Влияние состояния стенок труб на величину потерь и на коэффициент трения было предложено учитывать через высоту неровностей (шероховатостей) стенок . Однако совершенно очевидно, что чем меньше диаметр трубы, тем быстрее частицы жидкости, находящейся на оси потока, достигнут стенок и столкнутся с выступами шероховатости, и отразившись от них, вызовут возмущение (образование вихрей) в потоке жидкости. Поэтому напрашивается вывод о том, что частота вихреобразования при малых диаметрах труб больше и шероховатость той же высоты в малых трубах проявляется сильнее, чем в трубах большего диаметра. Поэтому вместо абсолютной шероховатости было введено понятие относительной шероховатости , равной отношению абсолютной шероховатости к диаметру трубы , т.е. . Как видно из приведенных графиков, всю область для критерия Рейнольдса можно разбить на четыре участка (I-IV). На первом участке, который простирается до первого граничного значения критерия , коэффициент трения λ не зависит от относительной шероховатости труб. Это объясняется наличием у стенок толстого пограничного слоя, в котором течение является ламинарным. Неровности стенок труб полностью закрыты этим слоем и не генерируют вихрей. Для этой зоны ; На четвертом участке от значений критерия коэффициент гидравлического трения не зависит от режима течения (является автомодельным по отношению к режиму течения), он зависит лишь от величины относительной шероховатости. Объясняется это тем, что толщина пограничного слоя, становится настолько малой, что слой не закрывает неровности стенки и они являются мощными генераторами вихрей в потоке жидкости. Начало этой зоны зависит от высоты шероховатостей и предложено определять как . Для этой автомодельной зоны коэффициент трения может быть рассчитан по уравнению Шифренсона: Эта зона носит еще название зоны квадратичного закона сопротивления т.к. величина гидравлических потерь пропорциональна квадрату средней скорости потока. Зоны II и III являются зонами, где гидравлические потери зависят как от режима течения, так и от шероховатости стенок труб и каналов. Опыты позволили выявить, что в зависимости от скорости одна и та же стенка может быть и гидравлически гладкой (создавать меньше потерь на трение), и гидравлически шероховатой. Гидравлически гладкой стенка будет в том случае, если неровности стенки не выступают за границы ламинарного (вязкого) подслоя. Если они выступают, то стенка трубы является гидравлически шероховатой. Одна и та же стенка может быть и гидравлически гладкой, и гидравлически шероховатой, так как толщина вязкого подслоя изменяется в зависимости от скорости движения потока. Поэтому говорят, что существуют зоны гладкого и смешанного трения. Граница между этими зонами определяется вторым граничным значением критерия Рейнольдса . Тогда зона гладкого трения начинается со значений критерия 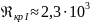и заканчивается при втором граничном числе Рейнольдса. В этой зоне для расчета коэффициента трения справедлива формула Блаузиуса: Зона смешанного трения (III зона на графиках Никурадзе) начинается при втором граничном числе Рейнольдса и завершается при третьем ( .). В этой зоне для расчета коэффициента Дарси применяют формулу Альтшуля: В зонах квадратичного закона сопротивления величина становится пренебрежимо малой по сравнению с относительной шероховатостью и формула Альтшуля принимает вид формулы Шифренсона (7.9).

При эксплуатации холодильных машин в пищевых производствах встречаются случаи, когда жидкость (холодильный агент) изменяет свою температуру при перемещении по трубам. Это же наблюдается и в технологическом оборудовании, где проводится термообработка жидких пищевых продуктов. Естественно, что изменение температуры влечет за собой изменение плотности и средней вязкости, что, в свою очередь, приводит к изменению профилей скорости. При таком неизотермическом движении потока коэффициент трения выражается через обычный коэффициент , для расчёта которого используют значение среды при ее средней температуре на данном участке: где и 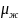– коэффициент динамической вязкости жидкости при температуре стенки и средней температуре жидкости соответственно.При неизометрическом движении газа можно пользоваться приближённой формулой Кутателадзе где T и Т_ст – соответственно средняя температура газа и стенки.

В конспекте по проще !!!!!!