
- •Класификация видов движения подвижных сред и методы описания движения жидкости (методы Эйлера и Лагранжа)
- •Кинематика жидкости. Основные понятия (линия тока, элементарная струйка) и определения (живое сечение струйки, смоченный периметр).
- •Поток и его характеристики: геометрич, кинематич, и режимные
- •Уравнение неразрывности для элементарной струйки и потока реальной жидкости. Понятия массового и объемного расхода.
- •Вывод дифер. Уравнений движения идеальной жидкости (уравнений Эйлера).
- •Уравнение Бернули для потока реальной жид. И его геометрич. И энергетич. Представление. Корректив кинетич. Энергии потока. Коэф. Кориолиса.
- •Диф. Ур. Движения реальных жид. (уравнение Новье-Стокса). Критери гидродинамического подобия
- •Опоты Рейнольдса. Критерии Рейнольдса. Ламин., турб, переходной режимы
- •Расчет расхода жидкости при ламинарном режиме ( уравнение Пуазеля)
- •Течение жидкости в малом зазоре. Уравнение Петрова.
- •Понятие местного сопротивления. Основные их виды. Расчет потерь напора на их преодоление. Эквивалентная длинна местных сопротивлений.
- •Внезапное расширение потока. Расчет потерь напора (уравнение Борда)
- •Простой трубопровод. Расчет потерь напора в трубопроводе. Кривые потребного напора простого трубопровода.
- •Понятие гидравлического удара. Формула Журавского. Определение величины повышения давления при прямом полном и неполном гидравлическом ударе.
- •Истечение жидкости через отверстие в тонкой стенке при постоянном напоре.
- •Истечение жидкости через насадок. Определение глубины вакуума в насадке.
- •28, 29, 30) Основная классификация гидромашин по силовому воздействию на жидкость. Насосы. Классификация насосов. Отличительные особенности насосов объёмного и динамического типов.
- •31) Основные технические показатели насосов.
- •3 2,33) Графические характеристики центробежных насосов. Главная характеристика насоса. Рабочая область насоса.
- •34) Устройство и принцип действия центробежного насоса. Трансформация д. Бернули в центробежном насосе. Запуск насоса в работу.
- •36) Основное уравнение центробежных машин. Теоретический и действительные напоры центробежного насоса.
- •37) Совместная работа насоса и трубопровода. Глубина всасывания насоса.
- •38)Насосная установка. Определение напора развиваемого насосом.
- •40) Работа насоса на сеть. Определение положения рабочей точки насоса.
- •41) Подбор центробежного насоса по каталогам. Методика подбора насоса для простого трубопровода.
- •43) Регулирование подачи центробежного насоса изменением характеристики сети. Другие методы регулирования подачи насоса и их анализ.
- •44) Регулирование подачи насоса изменений главной характеристикой насоса. Достоинства и недостатки главного метода.
- •45)Последовательное включение насосов в насосной установке. Построение результирующей характеристики установки и определение её рабочей точки.
- •46) Паралельное включение насосов в насосной установке. Построение результирующей характеристики установки и определение её рабочей точки.
- •47) Явление кавитации в насосных установках. Кавитационный запас. Уравнение Руднёва.
- •48) Шестерённые насосы. Устройство и принцип действия, главная характеристика.
- •49) Определение производительности шестерённого насоса. Методы регулирования подачи насоса.
- •50) Устройство и область применения и принцип работы инжектора. Определение коэффициента инжекции.
Вывод дифер. Уравнений движения идеальной жидкости (уравнений Эйлера).
В установившемся потоке идеальной жидкости
выделим элементарный объём в виде
параллелепипеда с размерами ребер dx,
dy, dz.
1)Так
как жидкость идеальная, то
установившемся потоке идеальной жидкости
выделим элементарный объём в виде
параллелепипеда с размерами ребер dx,
dy, dz.
1)Так
как жидкость идеальная, то
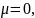 следовательно, касательные напряжения
следовательно, касательные напряжения
 и сила трения
и сила трения
 .
Из
поверхностных сил будет действовать
только сила давления P.
2)Из массовых (объёмных сил) действует
сила тяжести G,
dG=ρdVg.Применим
к выделенному в потоке элементарному
объёму основной принцип динамики: «Сумма
проекций сил, действующих на движущейся
элементарный объём жидкости, равна
произведению массы жидкости на её
ускорение». При перемещении вдоль оси
X(вызвано
перемещение действием сил давления):
.
Из
поверхностных сил будет действовать
только сила давления P.
2)Из массовых (объёмных сил) действует
сила тяжести G,
dG=ρdVg.Применим
к выделенному в потоке элементарному
объёму основной принцип динамики: «Сумма
проекций сил, действующих на движущейся
элементарный объём жидкости, равна
произведению массы жидкости на её
ускорение». При перемещении вдоль оси
X(вызвано
перемещение действием сил давления):
 (4.13);При перемещении вдоль оси
Y:
(4.13);При перемещении вдоль оси
Y: (5.14);При
перемещении вдоль оси Z:
(5.14);При
перемещении вдоль оси Z: (4.15);
Рассмотрим перемещение вдоль оси Х.
Сила гидростатического давления
(4.15);
Рассмотрим перемещение вдоль оси Х.
Сила гидростатического давления
 .
Выразим силу
.
Выразим силу
 через
через
 .Для этого определим единичное приращение
давления как
.Для этого определим единичное приращение
давления как
 ,
тогда изменение давления вдоль всего
ребра длинной
,
тогда изменение давления вдоль всего
ребра длинной
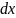 определяется как
определяется как
 .
Сила давления, действующая на правую
грань выделенного объема,
.
Сила давления, действующая на правую
грань выделенного объема, Подстановка
и
в уравнение (4.13) приводит к выражению
Подстановка
и
в уравнение (4.13) приводит к выражению
 ;Уравнение
(4.14) запишется аналогично:
;Уравнение
(4.14) запишется аналогично: А
уравнение (3.15) примет ид:
А
уравнение (3.15) примет ид: .
Масса жидкости, заключённая в элементарном
объёме параллелепипеда, определяется
как произведение:
.
Масса жидкости, заключённая в элементарном
объёме параллелепипеда, определяется
как произведение: А
проекции ускорения на соответствующие
координатные оси составят:
А
проекции ускорения на соответствующие
координатные оси составят: В
соответствии с основным принципом
динамики имеем систему уравнений:
В
соответствии с основным принципом
динамики имеем систему уравнений:
 ;
; ;
Или после сокращения система :
;
Или после сокращения система : (4.22). Система
(4.22) является системой дифференциальных
уравнений движения идеальной жидкости
для случая, когда из всех массовых сил
во внимание принята только сила тяжести
( Л.Эйлер 1755 г.).
(4.22). Система
(4.22) является системой дифференциальных
уравнений движения идеальной жидкости
для случая, когда из всех массовых сил
во внимание принята только сила тяжести
( Л.Эйлер 1755 г.).
Вывод уравнения Д. Бернули для установивш. движения идеальной жид-ти и анализ его составляющих. Систему дифференциальных уравнений Эйлера для потока идеальной (4.22) жидкости запишем в виде:
 ;
;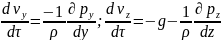 ;
;
 Соответственно
домножим уравнения системы (5.1) на dx
;dy;
dz
и осуществим почленное их сложение:
Соответственно
домножим уравнения системы (5.1) на dx
;dy;
dz
и осуществим почленное их сложение:
 ;
; Учитывая,
что выражение в скобках является полным
дифференциалом давления, т.е.:
Учитывая,
что выражение в скобках является полным
дифференциалом давления, т.е.: .
А
также то, что
.
А
также то, что
 получим
получим .Заменив
.Заменив
 получим
уравнение
получим
уравнение .Перенесём
в левую часть правую и введём постоянные
физические величины (плотность и
ускорение свободного падения) под знаки
дифференциалов:
.Перенесём
в левую часть правую и введём постоянные
физические величины (плотность и
ускорение свободного падения) под знаки
дифференциалов: Суммy
дифференциалов можно заменить
дифференциалом суммы:
Суммy
дифференциалов можно заменить
дифференциалом суммы: Откуда
Откуда Данное
уравнение является уравнением Бернулли
для струйки идеальной жидкости,
полученным им в 1738 г.Для двух различных
сечений струйки 1-1и 2-2 уравнение Бернулли
примет вид
Данное
уравнение является уравнением Бернулли
для струйки идеальной жидкости,
полученным им в 1738 г.Для двух различных
сечений струйки 1-1и 2-2 уравнение Бернулли
примет вид Для
элементарной струйки идеальной жидкости
полная удельная энергия есть величина
постоянная для всех сечений струйки.
Для
элементарной струйки идеальной жидкости
полная удельная энергия есть величина
постоянная для всех сечений струйки.
Э

 нергетич.
смысл и геометрич. интерпритация
уравнения Бернули для идеальной жид-ти.
Энергетический
смысл уравнения Бернулли:
Как известно, полная энергия потока
складывается из потенциальной энергии
положения Еz
и давления Ер,
а также кинетической энергии движения
Ек.
В свою очередь, потенциальная энергия
положения определяется как Еz=mgz;
энергия давления
нергетич.
смысл и геометрич. интерпритация
уравнения Бернули для идеальной жид-ти.
Энергетический
смысл уравнения Бернулли:
Как известно, полная энергия потока
складывается из потенциальной энергии
положения Еz
и давления Ер,
а также кинетической энергии движения
Ек.
В свою очередь, потенциальная энергия
положения определяется как Еz=mgz;
энергия давления
 ;
кинетическая энергия
;
кинетическая энергия
 .
Если энергией обладает единица веса
перекачиваемой жидкости, то в этом
случае говорят об удельной энергии
жидкости. Вес перекачиваемой жидкости
определяется из закона Ньютона как
G=mg.
Тогда удельная потенциальная энергия
(УПЭ) положения будет
выражена:УПЭ=Еп/G=mgz/(mg)=z.;
Удельная
потенциальная энергия давления
.
Если энергией обладает единица веса
перекачиваемой жидкости, то в этом
случае говорят об удельной энергии
жидкости. Вес перекачиваемой жидкости
определяется из закона Ньютона как
G=mg.
Тогда удельная потенциальная энергия
(УПЭ) положения будет
выражена:УПЭ=Еп/G=mgz/(mg)=z.;
Удельная
потенциальная энергия давления
 ;
Удельная кинетическая энергия потока
(УКЭ) идеальной жидкости будет равна:
;
Удельная кинетическая энергия потока
(УКЭ) идеальной жидкости будет равна: Полная
удельная энергия струйки идеальной
жидкости называется напором и представляет
собою сумму удельной потенциальной и
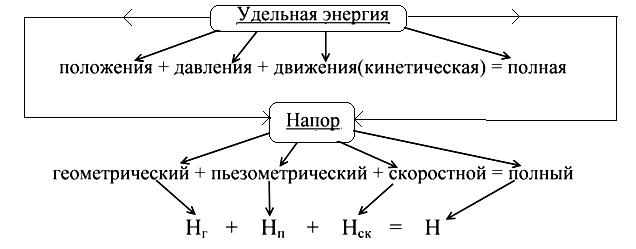
кинетической энергии. УПЭ+
УЭД+
УКЭ=УЭП
– уравнение энергетического баланса
потока.
Геометрическое
толкование уравнения Л.Бернулли.
Как
следует из уравнения
Полная
удельная энергия струйки идеальной
жидкости называется напором и представляет
собою сумму удельной потенциальной и
кинетической энергии. УПЭ+
УЭД+
УКЭ=УЭП
– уравнение энергетического баланса
потока.
Геометрическое
толкование уравнения Л.Бернулли.
Как
следует из уравнения
 ,
все его слагаемые имеют размерность
длины. Поэтому уравнению Бернулли
наряду с энергетическим толкованием
дается и геометрическое (см. рис).
В
потоке идеальной жидкости (
,
все его слагаемые имеют размерность
длины. Поэтому уравнению Бернулли
наряду с энергетическим толкованием
дается и геометрическое (см. рис).
В
потоке идеальной жидкости ( )
произвольно выберем сечениея 1-1, 2-2 и
3-3. В этих сечениях установим прямые
трубки (пьезометры) «а» и трубки с
изогнутым устьем навстречу потоку –
трубки «b»,
называемые трубками (пьезометрами)
полного напора. Жидкость в обоих трубках
поднимется на некоторую высоту. Причем
в трубках «b»
высота подъема будет больше ввиду
того, что трубка показывает помимо
давления в каждом сечении еще и учитывает
динамическое воздействие частиц
набегающей жидкости.
)
произвольно выберем сечениея 1-1, 2-2 и
3-3. В этих сечениях установим прямые
трубки (пьезометры) «а» и трубки с
изогнутым устьем навстречу потоку –
трубки «b»,
называемые трубками (пьезометрами)
полного напора. Жидкость в обоих трубках
поднимется на некоторую высоту. Причем
в трубках «b»
высота подъема будет больше ввиду
того, что трубка показывает помимо
давления в каждом сечении еще и учитывает
динамическое воздействие частиц
набегающей жидкости.
Линия,
проведенная по отметкам b1,
b2
и
b3
,будет называться линией
полных напоров,
а линия а1,
а2
и
а3
– линией
пьезометрических напоров.
Расстояние от плоскости сравнения 0-0
до центров выбранных сечений z1,
z2
и
z3
представляет собой геометрический
напор,
или нивелирную высоту.
 –
пьезометрический напор (высота),
отвечающий гидростатическому давлению
в рассматриваемом живом сечении.
–
пьезометрический напор (высота),
отвечающий гидростатическому давлению
в рассматриваемом живом сечении.
 –
динамический, или скоростной напор. Из
приведенного рисунка ясно, что трубка
«b»
измеряет полную удельную энергию потока,
а трубка «а» – только потенциальную.
Поэтому разность высот подъема жидкости
в пьезометрах «b»
и «а» указывает на удельную кинетическую
энергию потока. Здесь же стоит отметить
и тот факт, что при перемещении потока
от сечения 1-1 где его площадь S1,
до сечения 2-2, площадь которого S2,
скорость движения частиц соответственно
меняется от
–
динамический, или скоростной напор. Из
приведенного рисунка ясно, что трубка
«b»
измеряет полную удельную энергию потока,
а трубка «а» – только потенциальную.
Поэтому разность высот подъема жидкости
в пьезометрах «b»
и «а» указывает на удельную кинетическую
энергию потока. Здесь же стоит отметить
и тот факт, что при перемещении потока
от сечения 1-1 где его площадь S1,
до сечения 2-2, площадь которого S2,
скорость движения частиц соответственно
меняется от
 до
до
 .
Причем
.
Причем
 ,
а следовательно, скоростной напор в
первом сечении
,
а следовательно, скоростной напор в
первом сечении
 больше скоростного напора во втором
сечении
больше скоростного напора во втором
сечении
 .
При Z1=Z2
налицо переход кинетической энергии
потока во втором сечении в потенциальную.
Взаимный переход одного вида энергии
в другой и обратно называют трансформацией
Бернулли.
.
При Z1=Z2
налицо переход кинетической энергии
потока во втором сечении в потенциальную.
Взаимный переход одного вида энергии
в другой и обратно называют трансформацией
Бернулли.
